Introduction: Ever since I was initiated into Quantum Computing, through IBM’s Quantum Experience I have been hooked. My initial encounter with domain made me very excited and all wound up. The reason behind this, I think, is because there is an air of mystery around ‘Quantum’ anything. After my early rush with the Quantum Experience, I have deliberately slowed down to digest the heady stuff.
This post also includes my early prototype of a Quantum Computing Simulator( QCSimulator) which I am creating in R. I hope to have a decent Quantum Computing simulator available, in the next couple of months. The ideas for this simulator are based on IBM’s Quantum Experience and the lectures on Quantum Mechanics and Quantum Computation by Prof Umesh Vazirani from University of California at Berkeley at edX. This calls to this simulator have been included in R Markdown file and has been published at RPubs as Quantum Computing Simulator
Disclaimer: This article represents the author’s viewpoint only and doesn’t necessarily represent IBM’s positions, strategies or opinions
In this post I explore quantum gate operations
A) Quantum Gates
Quantum gates are represented as a n x n unitary matrix. In mathematics, a complex square matrix U is unitary if its conjugate transpose Uǂ is also its inverse – that is, if
U ǂU =U U ǂ=I
a) Clifford Gates
The following gates are known as Clifford Gates and are represented as the unitary matrix below
1. Pauli X
2.Pauli Y
3. Pauli Z
4. Hadamard
1/√2
5. S Gate
6. S1 Gate
7. CNOT
b) Non-Clifford Gate
The following are the non-Clifford gates
1. Toffoli Gate
T =
2. Toffoli1 Gate
T1 =
B) Evolution of a 1 qubit Quantum System
The diagram below shows how a 1 qubit system evolves on the application of Quantum Gates.
C) Evolution of a 2 Qubit System
The following diagram depicts the evolution of a 2 qubit system. The 4 different maximally entangled states can be obtained by using a Hadamard and a CNOT gate to |00>, |01>, |10> & |11> resulting in the entangled states Φ+, Ψ+, Φ–, Ψ– respectively
D) Verifying Unitary’ness
XXǂ = XǂX= I
TTǂ = TǂT=I
SSǂ = SǂS=I
The Uǂ function in the simulator is
Uǂ = GateDagger(U)
E) A look at some Simulator functions
The unitary functions for the Clifford and non-Clifford gates have been implemented functions. The unitary functions can be chained together by invoking each successive Gate as argument to the function.
1. Creating the dagger function
HDagger = GateDagger(Hadamard)
HDagger x Hadamard
TDagger = GateDagger(TGate)
TDagger x TGate
H## [,1] [,2]
## [1,] 0.7071068 0.7071068
## [2,] 0.7071068 -0.7071068HDagger = GateDagger(H)
HDagger## [,1] [,2]
## [1,] 0.7071068 0.7071068
## [2,] 0.7071068 -0.7071068HDagger %*% H## [,1] [,2]
## [1,] 1 0
## [2,] 0 1T## [,1] [,2]
## [1,] 1+0i 0.0000000+0.0000000i
## [2,] 0+0i 0.7071068+0.7071068iTDagger = GateDagger(T)
TDagger## [,1] [,2]
## [1,] 1+0i 0.0000000+0.0000000i
## [2,] 0+0i 0.7071068-0.7071068iTDagger %*% T## [,1] [,2]
## [1,] 1+0i 0+0i
## [2,] 0+0i 1+0i2. Angle between 2 vectors – Inner product
The angle between 2 vectors can be obtained by taking the inner product between the vectors
#1. a is the diagonal vector 1/2 |0> + 1/2 |1> and b = q0 = |0>
diagonal <- matrix(c(1/sqrt(2),1/sqrt(2)),nrow=2,ncol=1)
q0=matrix(c(1,0),nrow=2,ncol=1)
innerProduct(diagonal,q0)## [,1]
## [1,] 45#2. a = 1/2|0> + sqrt(3)/2|1> and b= 1/sqrt(2) |0> + 1/sqrt(2) |1>
a = matrix(c(1/2,sqrt(3)/2),nrow=2,ncol=1)
b = matrix(c(1/sqrt(2),1/sqrt(2)),nrow=2,ncol=1)
innerProduct(a,b)## [,1]
## [1,] 153. Chaining Quantum Gates
For e.g.
H x q0
S x H x q0 == > SGate(Hadamard(q0))
Or
H x S x S x H x q0 == > Hadamard(SGate(SGate(Hadamard))))
# H x q0
Hadamard(q0)## [,1]
## [1,] 0.7071068
## [2,] 0.7071068# S x H x q0
SGate(Hadamard(q0))## [,1]
## [1,] 0.7071068+0.0000000i
## [2,] 0.0000000+0.7071068i# H x S x S x H x q0
Hadamard(SGate(SGate(Hadamard(q0))))## [,1]
## [1,] 0+0i
## [2,] 1+0i# S x T x H x T x H x q0
SGate(TGate(Hadamard(TGate(Hadamard(q0)))))## [,1]
## [1,] 0.8535534+0.3535534i
## [2,] 0.1464466+0.3535534i4. Measurement
The output of Quantum Gate operations can be measured with
measurement(a)
measurement(q0)
measurement(Hadamard(q0))
a=SGate(TGate(Hadamard(TGate(Hadamard(I)))))
measurement(a)
measurement(SGate(TGate(Hadamard(TGate(Hadamard(I))))))
measurement(q0)## 0 1
## v 1 0measurement(Hadamard(q0))## 0 1
## v 0.5 0.5a <- SGate(TGate(Hadamard(TGate(Hadamard(q0)))))
measurement(a)## 0 1
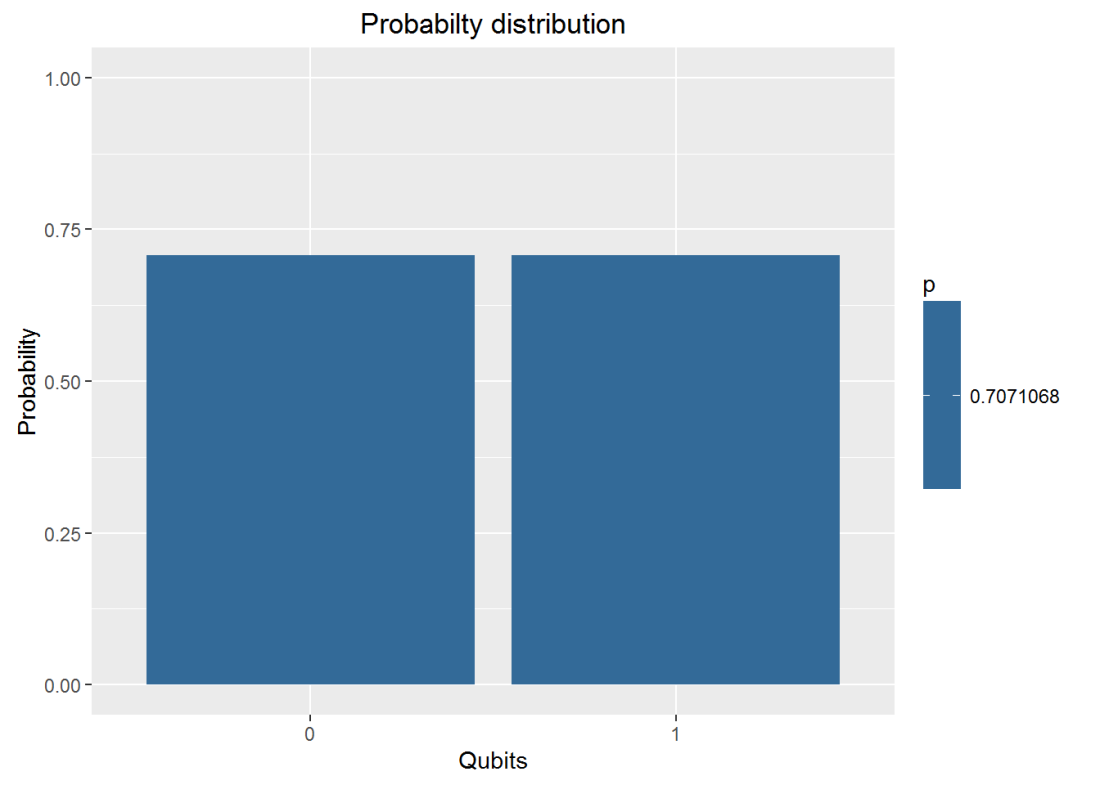
## v 0.8535534 0.14644665. Plot the measurements
plotMeasurement(q1)plotMeasurement(Hadamard(q0))a = measurement(SGate(TGate(Hadamard(TGate(Hadamard(q0))))))
plotMeasurement(a)6. Using the QCSimulator for one of the Bell tests
Here I compute the following measurement of Bell state ZW with the QCSimulator

When this is simulated on IBM’s Quantum Experience the result is

Below I simulate the same on my R based QCSimulator
# Compute the effect of the Composite H gate with the Identity matrix (I)
a=kronecker(H,I,"*")
a## [,1] [,2] [,3] [,4]
## [1,] 0.7071068 0.0000000 0.7071068 0.0000000
## [2,] 0.0000000 0.7071068 0.0000000 0.7071068
## [3,] 0.7071068 0.0000000 -0.7071068 0.0000000
## [4,] 0.0000000 0.7071068 0.0000000 -0.7071068# Compute the applcation of CNOT on this result
b = CNOT(a)
b## [,1] [,2] [,3] [,4]
## [1,] 0.7071068 0.0000000 0.7071068 0.0000000
## [2,] 0.0000000 0.7071068 0.0000000 0.7071068
## [3,] 0.0000000 0.7071068 0.0000000 -0.7071068
## [4,] 0.7071068 0.0000000 -0.7071068 0.0000000# Obtain the result of CNOT on q00
c = b %*% q00
c## [,1]
## [1,] 0.7071068
## [2,] 0.0000000
## [3,] 0.0000000
## [4,] 0.7071068# Compute the effect of the composite HxTxHxS gates and the Identity matrix(I) for measurement
d=Hadamard(TGate(Hadamard(SGate(I))))
e=kronecker(I, d,"*")
# Applying the composite gate on the output 'c'
f = e %*% c
# Measure the output
g <- measurement(f)
g## 00 01 10 11
## v 0.4267767 0.0732233 0.0732233 0.4267767#Plot the measurement
plotMeasurement(g)
aa
which is exactly the result obtained with IBM’s Quantum Experience!
Conclusion : In this post I dwell on 1 and 2-qubit quantum gates and explore their operation. I have started to construct a R based Quantum Computing Simulator. I hope to have a reasonable simulator in the next couple of months. Let’s see.
Watch this space!
Disclaimer: This article represents the author’s viewpoint only and doesn’t necessarily represent IBM’s positions, strategies or opinions
References
1. IBM Quantum Experience – User Guide
2. Quantum Mechanics and Quantum Conputing, UC Berkeley
Also see
1. Venturing into IBM’s Quantum Experience
2. Going deeper into IBM’s Quantum Experience!
3. A primer on Qubits, Quantum gates and Quantum Operations
You may also like
1. My TEDx talk on the “Internet of Things”
2. Experiments with deblurring using OpenCV
3. TWS-5: Google’s Page Rank: Predicting the movements of a random web walker
For more posts see
Index of posts





15 thoughts on “Exploring Quantum Gate operations with QCSimulator”