Optimal Deep Learning model selection using wandb.ai

In this post I use Weights and Biases’ wandb.ai ‘sweep’ feature, to automatically select the best Deep Learning model out of a set of models created through Grid Search. I chanced upon the Weights and Biases site when I was training and fine-tuning the T5 transformer model, on Kaggle, for my post GenerativeAI:Using T5 Transformer model to summarise Indian Philosophy. During this process Kaggle had requested for a token from wandb.ai.

Out of curiosity, I started to explore this Weights and Biases (W&B) machine learning site and was impressed with the visualisation capabilities of this site. So I decided to give weights and biases a try. It is quite interesting to see the live visualisation features of the site and it is becomes very easy to select the optimal model when we are trying to do a Grid search or Random search through a combination of hyper-parameters.

For this purpose, I used my processed T20 match dataset which I had used to compute the Win Probability of T20 teams. For more details please see my post GooglyPlusPlus: Win Probability using Deep Learning and player embeddings

Searching through high dimensional hyperparameter spaces to find the most performant model can quickly get unwieldy. Hyperparameter sweeps provide an organised and efficient way to automatically search through combinations of hyperparameter values (e.g. learning rate, batch size, epochs, dropout, optimizer type) to find the most optimal values.

Here are the steps

a) Install, import

!pip install wandb -qU

import wandb
from wandb.keras import WandbCallback
wandb.login()

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from pathlib import Path
import matplotlib.pyplot as plt

b) Load the dataset

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers

df1=pd.read_csv('t20.csv')
print("Shape of dataframe=",df1.shape)

train_dataset = df1.sample(frac=0.8,random_state=0)
test_dataset = df1.drop(train_dataset.index)
train_dataset1 = train_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_dataset1 = test_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
train_dataset1
train_labels = train_dataset.pop('isWinner')
test_labels = test_dataset.pop('isWinner')
train_dataset1

a=train_dataset1.describe()
stats=a.transpose
a

Shape of dataframe= (1359888, 10)
batsmanIdx	bowlerIdx	ballNum	ballsRemaining	runs	runRate	numWickets	runsMomentum	perfIndex
count	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06	1.087910e+06
mean	2.561058e+03	1.939449e+03	1.185352e+02	6.001942e+01	8.110290e+01	1.611611e+00	2.604912e+00	2.886850e-01	9.619675e+00
std	1.479446e+03	1.095097e+03	6.934078e+01	3.514725e+01	4.977998e+01	2.983874e+00	2.195410e+00	6.066070e-01	4.602859e+00
min	1.000000e+00	1.000000e+00	1.000000e+00	1.000000e+00	-5.000000e+00	-5.000000e+00	0.000000e+00	3.571429e-02	0.000000e+00
25%	1.230000e+03	9.400000e+02	5.900000e+01	3.000000e+01	4.100000e+01	1.043478e+00	1.000000e+00	1.058824e-01	6.539326e+00
50%	2.492000e+03	1.919000e+03	1.170000e+02	5.900000e+01	7.800000e+01	1.300000e+00	2.000000e+00	1.408451e-01	9.246753e+00
75%	3.868000e+03	2.884000e+03	1.770000e+02	9.000000e+01	1.170000e+02	1.590312e+00	4.000000e+00	2.352941e-01	1.218349e+01
max	5.226000e+03	3.848000e+03	2.860000e+02	1.610000e+02	2.780000e+02	2.510000e+02	1.000000e+01	1.100000e+01	6.600000e+01

c) Define the Deep Learning model

import pandas as pd
import numpy as np
from keras.layers import Input, Embedding, Flatten, Dense
from keras.models import Model
from keras.layers import Input, Embedding, Flatten, Dense, Reshape, Concatenate, Dropout
from keras.models import Model

tf.random.set_seed(432)
# create input layers for each of the predictors
batsmanIdx_input = Input(shape=(1,), name='batsmanIdx')
bowlerIdx_input = Input(shape=(1,), name='bowlerIdx')
ballNum_input = Input(shape=(1,), name='ballNum')
ballsRemaining_input = Input(shape=(1,), name='ballsRemaining')
runs_input = Input(shape=(1,), name='runs')
runRate_input = Input(shape=(1,), name='runRate')
numWickets_input = Input(shape=(1,), name='numWickets')
runsMomentum_input = Input(shape=(1,), name='runsMomentum')
perfIndex_input = Input(shape=(1,), name='perfIndex')

# Set the embedding size
no_of_unique_batman=len(df1["batsmanIdx"].unique())
print(no_of_unique_batman)
no_of_unique_bowler=len(df1["bowlerIdx"].unique())
print(no_of_unique_bowler)
embedding_size_bat = no_of_unique_batman ** (1/4)
embedding_size_bwl = no_of_unique_bowler ** (1/4)


# create embedding layer for the categorical predictor
batsmanIdx_embedding = Embedding(input_dim=no_of_unique_batman+1, output_dim=16,input_length=1)(batsmanIdx_input)
batsmanIdx_flatten = Flatten()(batsmanIdx_embedding)
bowlerIdx_embedding = Embedding(input_dim=no_of_unique_bowler+1, output_dim=16,input_length=1)(bowlerIdx_input)
bowlerIdx_flatten = Flatten()(bowlerIdx_embedding)

# concatenate all the predictors
x = keras.layers.concatenate([batsmanIdx_flatten,bowlerIdx_flatten, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input])

# add hidden layers
x = Dense(64, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(32, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(16, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(8, activation='relu')(x)
x = Dropout(0.1)(x)
# add output layer
output = Dense(1, activation='sigmoid', name='output')(x)
print(output.shape)
# create model

# Initialize a new W&B run
#run = wandb.init(project='t20', group='cricket')

model = Model(inputs=[batsmanIdx_input,bowlerIdx_input, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input], outputs=output)
model.summary()

# Initialize a new W&B run
run = wandb.init(project='t20', group='cricket')
wandb.init(
    # set the wandb project where this run will be logged
    project="t20",

    # track hyperparameters and run metadata
    config={
    "learning_rate": 0.02,
    "dropout": 0.01,
    "batch_size": 1024,
    "epochs": 5,
    }
)


5226
3848
(None, 1)
Model: "model"
__________________________________________________________________________________________________
 Layer (type)                Output Shape                 Param #   Connected to                  
==================================================================================================
 batsmanIdx (InputLayer)     [(None, 1)]                  0         []                            
                                                                                                  
 bowlerIdx (InputLayer)      [(None, 1)]                  0         []                            
                                                                                                  
 embedding (Embedding)       (None, 1, 16)                83632     ['batsmanIdx[0][0]']          
                                                                                                  
 embedding_1 (Embedding)     (None, 1, 16)                61584     ['bowlerIdx[0][0]']           
                                                                                                  
 flatten (Flatten)           (None, 16)                   0         ['embedding[0][0]']           
                                                                                                  
 flatten_1 (Flatten)         (None, 16)                   0         ['embedding_1[0][0]']         
                                                                                                  
 ballNum (InputLayer)        [(None, 1)]                  0         []                            
                                                                                                  
 ballsRemaining (InputLayer  [(None, 1)]                  0         []                            
 )                                                                                                
                                                                                                  
 runs (InputLayer)           [(None, 1)]                  0         []                            
                                                                                                  
 runRate (InputLayer)        [(None, 1)]                  0         []                            
                                                                                                  
 numWickets (InputLayer)     [(None, 1)]                  0         []                            
                                                                                                  
 runsMomentum (InputLayer)   [(None, 1)]                  0         []                            
                                                                                                  
 perfIndex (InputLayer)      [(None, 1)]                  0         []                            
                                                                                                  
 concatenate (Concatenate)   (None, 39)                   0         ['flatten[0][0]',             
                                                                     'flatten_1[0][0]',           
                                                                     'ballNum[0][0]',             
                                                                     'ballsRemaining[0][0]',      
                                                                     'runs[0][0]',                
                                                                     'runRate[0][0]',             
                                                                     'numWickets[0][0]',          
                                                                     'runsMomentum[0][0]',        
                                                                     'perfIndex[0][0]']           
                                                                                                  
 dense (Dense)               (None, 64)                   2560      ['concatenate[0][0]']         
                                                                                                  
 dropout (Dropout)           (None, 64)                   0         ['dense[0][0]']               
                                                                                                  
 dense_1 (Dense)             (None, 32)                   2080      ['dropout[0][0]']             
                                                                                                  
 dropout_1 (Dropout)         (None, 32)                   0         ['dense_1[0][0]']             
                                                                                                  
 dense_2 (Dense)             (None, 16)                   528       ['dropout_1[0][0]']           
                                                                                                  
 dropout_2 (Dropout)         (None, 16)                   0         ['dense_2[0][0]']             
                                                                                                  
 dense_3 (Dense)             (None, 8)                    136       ['dropout_2[0][0]']           
                                                                                                  
 dropout_3 (Dropout)         (None, 8)                    0         ['dense_3[0][0]']             
                                                                                                  
 output (Dense)              (None, 1)                    9         ['dropout_3[0][0]']           
                                                                                                  
==================================================================================================
Total params: 150529 (588.00 KB)
Trainable params: 150529 (588.00 KB)
Non-trainable params: 0 (0.00 Byte)

d) Create a Training script

def get_optimizer(lr=1e-2, optimizer="adam"):
    "Select optmizer between adam and sgd with momentum"
    if optimizer.lower() == "adam":
        return tf.keras.optimizers.Adam(learning_rate=lr)
    if optimizer.lower() == "sgd":
        return tf.keras.optimizers.SGD(learning_rate=lr, momentum=0.1)

def train(model, batch_size=1024, epochs=10, lr=1e-2, optimizer='adam', log_freq=10):

    # Compile model like you usually do.
    tf.keras.backend.clear_session()
    model.compile(loss="binary_crossentropy",
                  optimizer=get_optimizer(lr, optimizer),
                  metrics=["accuracy"])

    # callback setup
    cbs = [WandbCallback(data_type='auto', log_batch_frequency=None)]

    # train the model
    history=model.fit([train_dataset1['batsmanIdx'],train_dataset1['bowlerIdx'],train_dataset1['ballNum'],train_dataset1['ballsRemaining'],train_dataset1['runs'],
           train_dataset1['runRate'],train_dataset1['numWickets'],train_dataset1['runsMomentum'],train_dataset1['perfIndex']], train_labels, epochs=epochs, batch_size=batch_size,callbacks=cbs,
          validation_data = ([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']],test_labels), verbose=1)

e) Define the sweep for Grid Search

#Grid search
sweep_config = {
    'method': 'grid'
    }

metric = {
    'name': 'val_loss',
    'goal': 'minimize'
    }

sweep_config['metric'] = metric
# Optimizers - Adam, SGD
parameters_dict = {
    'optimizer': {
        'values': ['adam', 'sgd']
        },
    'dropout': {
          'values': [0.1, 0.05]
        },
    }

sweep_config['parameters'] = parameters_dict

parameters_dict.update({
    'epochs': {
        'value': 20}
    })

import math
# Set learning_rate, batch_size
parameters_dict.update({
    'learning_rate': {
         'values': [0.005,0.008,0.01,.03]  
      },
    'batch_size': {
        'values': [1024,2048]
      }
    })

import pprint
pprint.pprint(sweep_config)

'method': 'grid',
 'metric': {'goal': 'minimize', 'name': 'val_loss'},
 'parameters': {'batch_size': {'values': [1024, 2048]},
                'dropout': {'values': [0.1, 0.05]},
                'epochs': {'value': 20},
                'learning_rate': {'values': [0.005, 0.008, 0.01, 0.03]},
                'optimizer': {'values': ['adam', 'sgd']}}}

f) Wrap the Training Loop


def sweep_train(config_defaults=None):
    # Initialize wandb with a sample project name
    with wandb.init(config=config_defaults):  # this gets over-written in the Sweep

        # Specify the other hyperparameters to the configuration, if any
        wandb.config.architecture_name = "DL"
        wandb.config.dataset_name = "T20"
        # initialize model
        #model = T20Net(wandb.config.dropout)

        train(model,
              wandb.config.batch_size,
              wandb.config.epochs,
              wandb.config.learning_rate,
              wandb.config.optimizer)

g) Initialise Sweep and Run Agent

sweep_id = wandb.sweep(sweep_config, project="sweeps-keras-t20")

wandb.agent(sweep_id, sweep_train, count=10)

wandb: WARNING Calling wandb.login() after wandb.init() has no effect.
wandb: Agent Starting Run: zbaaq0bn with config:
wandb: 	batch_size: 1024
wandb: 	dropout: 0.1
wandb: 	epochs: 20
wandb: 	learning_rate: 0.005
wandb: 	optimizer: adam

Epoch 19/20
1061/1063 [============================>.] - ETA: 0s - loss: 0.3073 - accuracy: 0.8490/usr/local/lib/python3.10/dist-packages/keras/src/engine/training.py:3000: UserWarning: You are saving your model as an HDF5 file via `model.save()`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')`.
  saving_api.save_model(
wandb: Adding directory to artifact (/content/wandb/run-20231004_065327-zbaaq0bn/files/model-best)... Done. 0.0s
1063/1063 [==============================] - 15s 14ms/step - loss: 0.3073 - accuracy: 0.8490 - val_loss: 0.3093 - val_accuracy: 0.8479
Epoch 20/20
1062/1063 [============================>.] - ETA: 0s - loss: 0.3052 - accuracy: 0.8502/usr/local/lib/python3.10/dist-packages/keras/src/engine/training.py:3000: UserWarning: You are saving your model as an HDF5 file via `model.save()`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')`.
  saving_api.save_model(
wandb: Adding directory to artifact (/content/wandb/run-20231004_065327-zbaaq0bn/files/model-best)... Done. 0.0s
1063/1063 [==============================] - 18s 17ms/step - loss: 0.3052 - accuracy: 0.8502 - val_loss: 0.3068 - val_accuracy: 0.8490
Waiting for W&B process to finish... (success).
Run history:

accuracy	▁▅▅▆▆▆▇▇▇▇▇▇▇███████
epoch	▁▁▂▂▂▃▃▄▄▄▅▅▅▆▆▇▇▇██
loss	█▅▄▃▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁
val_accuracy	▁▂▃▄▄▅▅▅▆▆▆▇▇▇▇▇▇███
val_loss	█▆▅▅▄▄▃▃▃▃▃▂▂▂▂▂▂▁▁▁

Run summary:

accuracy	0.85022
best_epoch	19
best_val_loss	0.30681
epoch	19
loss	0.30521
val_accuracy	0.849
val_loss	0.30681

...
...
wandb: Agent Starting Run: 4qtyxzq9 with config:
wandb: 	batch_size: 1024
wandb: 	dropout: 0.1
wandb: 	epochs: 20
wandb: 	learning_rate: 0.008
wandb: 	optimizer: sgd
...
...

Epoch 18/20
1063/1063 [==============================] - 13s 12ms/step - loss: 0.2672 - accuracy: 0.8697 - val_loss: 0.2819 - val_accuracy: 0.8624
Epoch 19/20
1061/1063 [============================>.] - ETA: 0s - loss: 0.2669 - accuracy: 0.8697/usr/local/lib/python3.10/dist-packages/keras/src/engine/training.py:3000: UserWarning: You are saving your model as an HDF5 file via `model.save()`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')`.
  saving_api.save_model(
wandb: Adding directory to artifact (/content/wandb/run-20231004_070920-4qtyxzq9/files/model-best)... Done. 0.0s
1063/1063 [==============================] - 14s 13ms/step - loss: 0.2669 - accuracy: 0.8697 - val_loss: 0.2813 - val_accuracy: 0.8635
Epoch 20/20
1063/1063 [==============================] - 13s 12ms/step - loss: 0.2650 - accuracy: 0.8707 - val_loss: 0.2957 - val_accuracy: 0.8557
Waiting for W&B process to finish... (success).
6.805 MB of 6.818 MB uploaded (0.108 MB deduped)
Run history:

accuracy	▁▂▃▃▄▄▄▄▄▄▄▄▅▅▄▆▅▆▆█
epoch	▁▁▂▂▂▃▃▄▄▄▅▅▅▆▆▇▇▇██
loss	█▇▆▆▅▅▅▅▅▅▅▄▄▄▄▄▄▃▃▁
val_accuracy	▇▅▅▁█▅▇▆▆▅█▅▅▆▃▇▁▇█▁
val_loss	▃▄▄▅▁▃▂▃▃▃▁▄▄▂▆▂█▁▁█

Run summary:

accuracy	0.87067
best_epoch	18
best_val_loss	0.28127
epoch	19
loss	0.26499
val_accuracy	0.85565
val_loss	0.29573
...
...
wandb: Agent Starting Run: lt2fknva with config:
wandb: 	batch_size: 1024
wandb: 	dropout: 0.1
wandb: 	epochs: 20
wandb: 	learning_rate: 0.01
wandb: 	optimizer: adam
Tracking run with wandb version 0.15.11
Run data is saved locally in /content/wandb/run-20231004_071359-lt2fknva
Syncing run lively-sweep-5 to Weights & Biases (docs)
...
...
Epoch 19/20
1063/1063 [==============================] - 14s 13ms/step - loss: 0.2779 - accuracy: 0.8651 - val_loss: 0.2883 - val_accuracy: 0.8607
Epoch 20/20
1060/1063 [============================>.] - ETA: 0s - loss: 0.2795 - accuracy: 0.8643/usr/local/lib/python3.10/dist-packages/keras/src/engine/training.py:3000: UserWarning: You are saving your model as an HDF5 file via `model.save()`. This file format is considered legacy. We recommend using instead the native Keras format, e.g. `model.save('my_model.keras')`.
  saving_api.save_model(
wandb: Adding directory to artifact (/content/wandb/run-20231004_071359-lt2fknva/files/model-best)... Done. 0.0s
1063/1063 [==============================] - 16s 15ms/step - loss: 0.2795 - accuracy: 0.8643 - val_loss: 0.2831 - val_accuracy: 0.8620
Waiting for W&B process to finish... (success).
Run history:

accuracy	▁▁▁▂▂▃▃▄▅▅▅▆▆▆▆▆▇▇█▇
epoch	▁▁▂▂▂▃▃▄▄▄▅▅▅▆▆▇▇▇██
loss	███▇▇▆▅▆▅▄▄▃▃▃▃▂▂▂▁▂
val_accuracy	▁▅▂▆▆▅▂▆▆▅▇▇▆▇▅▃▃▆▇█
val_loss	▇▆▇▅▃▅█▆▅▄▂▃▄▂▆▆▇▃▃▁

Run summary:

accuracy	0.8643
best_epoch	19
best_val_loss	0.28309
epoch	19
loss	0.27949
val_accuracy	0.86195
val_loss	0.28309
...
...

In the W & B site each of the runs or captured very nicely

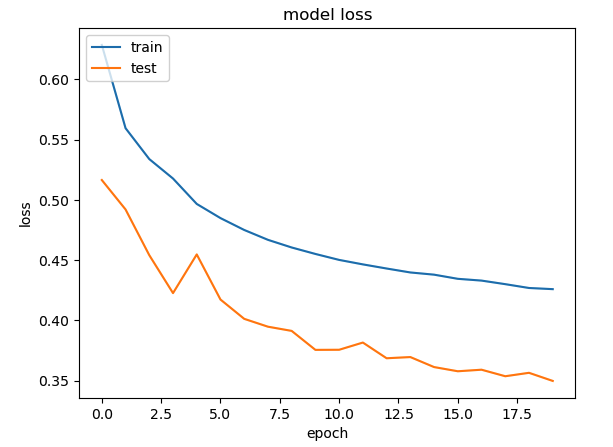
The best model is ‘lively-sweep-5‘ with the lowest validation loss

The picture below gives the validation loss for various combinations of the hyper-para meters

It is very easy to visually pick the best model with loss as shown below. It is lively-sweep-5. we can see the values of the hyper-parameters for this DL model

Details of optimal Deep Learning model

a. Run – lively-sweep-5

b. optimizer – adam

c. learning_rate – 0.01

d. batch_size – 1024

e. dropout – 0.1

We can see the performance of this model individually by clicking lively-sweep-6 on the left panel

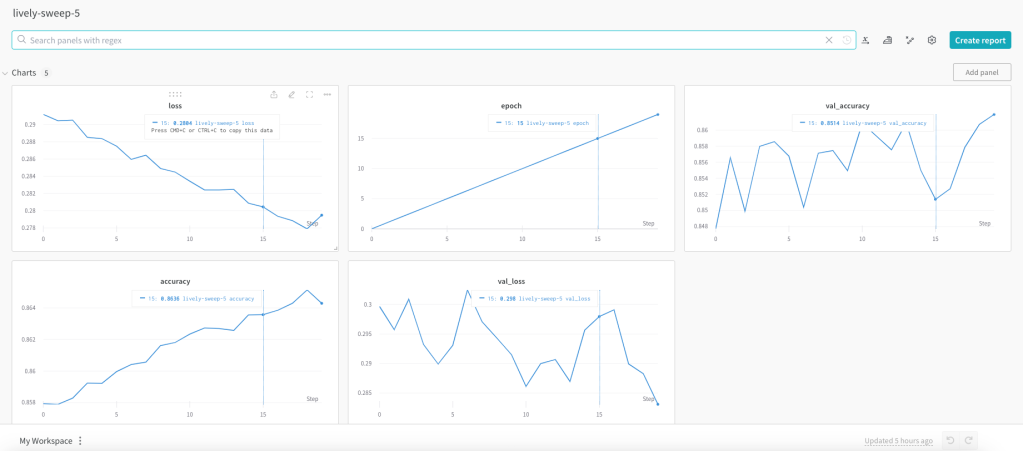
It was good fun to play around with the Weights and Biases in selecting an optimal model

Identifying cricketing shots using AI

Image classification using Deep Learning has been around for almost a decade. In fact, this field with the use of Convolutional Neural Networks (CNN) is quite mature and the algorithms work very well in image classification, object detection, facial recognition and self-driving cars. In this post, I use AI image classification to identify cricketing shots. While the problem falls in a well known domain, the application of image classification in identifying cricketing shots is probably new. I have selected three cricketing shots, namely, the front drive, sweep shot, and the hook shot for this purpose. My purpose was to build a proof-of-concept and not a perfect product. I have kept the dataset deliberately small (for obvious reasons) of just about 14 samples for each cricketing shot, and for a total of about 41 total samples for both training and test data. Anyway, I get a reasonable performance from the AI model.

Included below are some examples of the data set

This post is based on this or on Image classification from Hugging face. Interestingly, this, the model used here is based on Vision Transformers (ViT from Google Brain) and not on Convolutional Neural Networks as is usually done.

The steps are to fine-tune ViT Transformer with the ‘strokes’ dataset are

Install the necessary libraries

! pip install transformers[torch] datasets evaluate accelerate -U
! pip install -U accelerate
! pip install -U transformers

b) Login to Hugging Face account

 from huggingface_hub import notebook_login
notebook_login()

Login successful

c) Load the batting strokes dataset with 41 images

from datasets import load_dataset
df1 = load_dataset("tvganesh/strokes",split='train')
type(df1)
len(df1)

41

df1
Dataset({
    features: ['image', 'label'],
    num_rows: 41
})

d) Create a dictionary that maps the label name to an integer and vice versa. Display the labels

labels = df1.features["label"].names
label2id, id2label = dict(), dict()
for i, label in enumerate(labels):
label2id[label] = str(i)
id2label[str(i)] = label

labels

['front drive', 'hook shot', 'sweep shot']

e) Load ViT image processor. To apply the correct transformations, ImageProcessor is initialised with a configuration that was saved along with the pretrained model

from transformers import AutoImageProcessor

checkpoint = "google/vit-base-patch16-224-in21k"
image_processor = AutoImageProcessor.from_pretrained(checkpoint)

f) Apply image transformations to the images to make the model more robust against overfitting

from torchvision.transforms import RandomResizedCrop, Compose, Normalize, ToTensor

normalize = Normalize(mean=image_processor.image_mean, std=image_processor.image_std)
size = (
    image_processor.size["shortest_edge"]
    if "shortest_edge" in image_processor.size
    else (image_processor.size["height"], image_processor.size["width"])
)
_transforms = Compose([RandomResizedCrop(size), ToTensor(), normalize])

g) Create a preprocessing function to apply the transforms and return pixel_values of the image as the inputs to the model – :

def transforms(examples):
    examples["pixel_values"] = [_transforms(img.convert("RGB")) for img in examples["image"]]
    del examples["image"]
    return examples

h) Apply the preprocessing function over the entire dataset, using Hugging Face Dataset’s ‘with_transform’ method

df1 = df1.with_transform(transforms)

from transformers import DefaultDataCollator
data_collator = DefaultDataCollator()

i) Evaluate model’s performance with evaluate

import evaluate
accuracy = evaluate.load("accuracy")

j) Calculate accuracy by passing in predictions and labels

import numpy as np
def compute_metrics(eval_pred):
    predictions, labels = eval_pred
    predictions = np.argmax(predictions, axis=1)
    return accuracy.compute(predictions=predictions, references=labels)

k) Load ViT by specifying the number of labels along with the number of expected labels, and the label mapping

 from transformers import AutoModelForImageClassification, TrainingArguments, Trainer

model = AutoModelForImageClassification.from_pretrained(
    checkpoint,
    num_labels=len(labels),
    id2label=id2label,
    label2id=label2id,
)

Pass the training arguments to Trainer along with the model, dataset, tokenizer, data collator, and compute_metrics function.
Call train() to finetune your model.

training_args = TrainingArguments(
    output_dir="data_classify",
    remove_unused_columns=False,
    evaluation_strategy="epoch",
    save_strategy="epoch",
    learning_rate=5e-5,
    per_device_train_batch_size=8,
    #gradient_accumulation_steps=4,
    per_device_eval_batch_size=6,
    num_train_epochs=20,
    warmup_ratio=0.1,
    logging_steps=10,
    load_best_model_at_end=True,
    metric_for_best_model="accuracy",
    push_to_hub=True,
)

trainer = Trainer(
    model=model,
    args=training_args,
    data_collator=data_collator,
    train_dataset=train_dataset,
    eval_dataset=test_dataset,
    tokenizer=image_processor,
    compute_metrics=compute_metrics,
)

trainer.train()

Epoch	Training Loss	Validation Loss	Accuracy
1	No log	0.434451	1.000000
2	No log	0.388312	1.000000
3	0.361200	0.409932	0.888889
4	0.361200	0.245226	1.000000
5	0.293400	0.196930	1.000000
6	0.293400	0.167858	1.000000
7	0.293400	0.140349	1.000000
8	0.203000	0.153016	1.000000
9	0.203000	0.116115	1.000000
10	0.150500	0.129171	1.000000
11	0.150500	0.103121	1.000000
12	0.150500	0.108433	1.000000
13	0.138800	0.107799	1.000000
14	0.138800	0.093700	1.000000
15	0.107600	0.100769	1.000000
16	0.107600	0.113148	1.000000
17	0.107600	0.100740	1.000000
18	0.104700	0.177483	0.888889
19	0.104700	0.084438	1.000000
20	0.090200	0.112654	1.000000
TrainOutput(global_step=80, training_loss=0.18118578270077706, metrics={'train_runtime': 176.3834, 'train_samples_per_second': 3.628, 'train_steps_per_second': 0.454, 'total_flos': 4.959531785650176e+16, 'train_loss': 0.18118578270077706, 'epoch': 20.0})

m) Push to Hub

trainer.push_to_hub()

You can try out my fine-tuned model at identify_stroke̱

Here are a couple of trials

As I mentioned before, the model should be reasonably accurate but not perfect, since my training dataset is extremely small. This is just a prototype to show that shot identification in cricket with AI is in the realm of the possible.

References

Do take a look at

To see all posts click Index of posts

T20 Win Probability using CTGANs, synthetic data

This should be my last post on computing T20 Win Probability. In this post I compute Win Probability using Augmented Data with the help of Conditional Tabular Generative Adversarial Networks (CTGANs).

A.Introduction

I started the computation of T20 match Win Probability in my earlier post

a) ‘Computing Win-Probability of T20 matches‘ where I used

vanilla Logistic Regression to get an accuracy of 0.67,
Random Forest with Tidy models gave me an accuracy of 0.737
Deep Learning with Keras also with 0.73.

This was done without player embeddings

b) Next I used player embeddings for batsmen and bowlers in my post Boosting Win Probability accuracy with player embeddings , and my accuracies improved significantly

glmnet : accuracy – 0.728 and roc_auc – 0.81
random forest : accuracy – 0.927 and roc_auc – 0.98
mlp-dnn :accuracy – 0.762 and roc_auc – 0.854

c) Third I tried using Deep Learning with Keras using player embeddings

DL network gave an accuracy of 0.8639

This was lightweight and could be easily deployed in my Shiny GooglyPlusPlus app as opposed to the Tidymodel’s Random Forest, which was bulky and slow.

d) Finally I decided to try and improve the accuracy of my Deep Learning Model using Synthetic data. Towards this end, my explorations led me to Conditional Tabular Generative Adversarial Networks (CTGANs). CTGAN are GAN networks that can be used with Tabular data as GAN models are not useful with tabular data. However, the best performance I got for

DL Keras Model + Synthetic data : accuracy =0.77

The poorer accuracy was because CTGAN requires enormous computing power (GPUs) and RAM. The free version of Colab, Kaggle kept crashing when I tried with even 0.1 % of my 1.2 million dataset size. Finally, I tried with just 0.05% and was able to generate synthetic data. Most likely, it is the small sample size and the smaller number of epochs could be the reason for the poor result. In any case, it was worth trying and this approach would possibly work with sufficient computing resources.

B.Generative Adversarial Networks (GANs)

Generative Adversarial Networks (GANs) was the brain child of Ian Goodfellow who demonstrated it in 2014. GANs are capable of generating synthetic text, tables, images, videos using available data. In Adversarial nets framework, the generative model is pitted against an adversary: a
discriminative model that learns to determine whether a sample is from the model distribution or the
data distribution.

GANs have 2 Deep Neural Networks , the Generator and Discriminator which compete against other

The Generator (Counterfeiter) takes random noise as input and generates fake images, tables, text. The generator learns to generate plausible data. The generated instances become negative training examples for the discriminator.
The Discriminator (Police) which tries to distinguish between the real and fake images, text. The discriminator learns to distinguish the generator’s fake data from real data. The discriminator penalises the generator for producing implausible results.

A pictorial representation of the GAN model can be shown below

Theoretically best performance of GANs are supposed to happen when the network reaches the ‘Nash equilibrium‘, i.e. when the Generator produces near fake images and the Discriminator’s loss is f ~0.5 i.e. the discriminator is unable to distinguish between real and fake images.

Note: Though I have mentioned T20 data in the above GAN model, the T20 tabular data is actually used in CTGAN which is slightly different from the above. See Reference 2) below.

C. Conditional Tabular Generative Adversial Networks (CTGANs)

“Modeling the probability distribution of rows in tabular data and generating realistic synthetic data is a non-trivial task. Tabular data usually contains a mix of discrete and continuous columns. Continuous columns may have multiple modes whereas discrete columns are sometimes imbalanced making the modeling difficult.” CTGANs handle these challenges.

I came upon CTGAN after spending some time exploring GANs via blogs, videos etc. For building the model I use real T20 match data. However, CTGAN requires immense raw computing power and a lot of RAM. My initial attempts on Colab, my Mac (12 core, 32GB RAM), took forever before eventually crashing, I switched to Kaggle and used GPUs. Still I was only able to use only a miniscule part of my T20 dataset. My match data has 1.2 million rows, hoanything > 0.05% resulted in Kaggle crashing. Since I was able to use only a fraction, I executed the CTGAN model over several iterations, each iteration with a random 0.05% sample of the dataset. At the end of each iterations I also generate synthetic dataset. Over 12 iterations, I generate close 360K of ‘synthetic‘ T20 match data.

I then augment the 1.2 million rows of ‘real‘ T20 match data with the generated ‘synthetic T20 match data to run my Deep Learning model

D. Executing the CTGAN model

a. Read the real T20 match data

!pip install ctgan
import pandas as pd
import ctgan
from ctgan import CTGAN
from numpy.random import seed

# Read the T20 match data
df = pd.read_csv('/kaggle/input/cricket1/t20.csv')

# Randomly sample 0.05% of the dataset. Note larger datasets cause the algo to crash
train_dataset = df.sample(frac=0.05)

# Print the real T20 match data
print(train_dataset.head(10))
print(train_dataset.shape)

             batsmanIdx  bowlerIdx  ballNum  ballsRemaining  runs   runRate  \
363695         3333        432      134             119   153  1.285714   
1082839        3881       1180      218              30    93  3.100000   
595799         2366        683      187              65   120  1.846154   
737614         4490       1381      148              87   144  1.655172   
410202          934       1003       19             106    35  1.842105   
525627          921       1711      251               1     8  8.000000   
657669         4718       1602      130             115   145  1.260870   
666461         4309       1989       44              87    38  0.863636   
651229         3336        754       30              92    36  1.200000   
709892         3048        421       97              28   119  1.226804   

            numWickets  runsMomentum  perfIndex  isWinner  
363695            0      0.092437  18.333333         1  
1082839           5      0.200000   4.736842         0  
595799            4      0.107692   9.566667         0  
737614            1      0.114943   9.130435         1  
410202            0      0.103774  20.263158         0  
525627            8      3.000000   3.837209         0  
657669            0      0.095652  19.555556         0  
666461            0      0.126437   9.500000         0  
651229            0      0.119565  13.200000         0  
709892            3      0.285714   9.814433         1  
(59956, 10)

b. Run CTGAN model on the real T20 data

import pandas as pd
import ctgan
from ctgan import CTGAN
from numpy.random import seed
from pickle import TRUE

df = pd.read_csv('/kaggle/input/cricket1/t20.csv')

#Specify the categorical features. batsmanIdx & bowlerIdx are player embeddings
categorical_features = ['batsmanIdx','bowlerIdx']

# Create a empty dataframe for synthetic data
df1 = pd.DataFrame()

# Loop for 12 iterations. Minimize generator & discriminator loss
for i in range(12):
    print(i)
    train_dataset = df.sample(frac=0.05)
    seed(33)

    ctgan = CTGAN(epochs=20,verbose=True,generator_lr=.001,discriminator_lr=.001,batch_size=1000)
    ctgan.fit(train_dataset, categorical_features)

    # Generate synthetic data
    samples = ctgan.sample(30000)

   # Concatenate the synthetic data after each iteration
    df1 = pd.concat([df1,samples])
    print(samples.head())
    print(df1.shape)

# Output the synthetic data to file
df1.to_csv("output1.csv",index=False)

0
Epoch 1, Loss G:  8.3825,Loss D: -0.6159
Epoch 2, Loss G:  3.5117,Loss D: -0.3016
Epoch 3, Loss G:  2.1619,Loss D: -0.5713
Epoch 4, Loss G:  0.9847,Loss D:  0.1010
Epoch 5, Loss G:  0.6198,Loss D:  0.0789
Epoch 6, Loss G:  0.1710,Loss D:  0.0959
Epoch 7, Loss G:  0.3236,Loss D: -0.1554
Epoch 8, Loss G:  0.2317,Loss D: -0.0765
Epoch 9, Loss G: -0.0127,Loss D:  0.0275
Epoch 10, Loss G:  0.1477,Loss D: -0.0353
Epoch 11, Loss G:  0.0997,Loss D: -0.0129
Epoch 12, Loss G:  0.0066,Loss D: -0.0486
Epoch 13, Loss G:  0.0351,Loss D: -0.0805
Epoch 14, Loss G: -0.1399,Loss D: -0.0021
Epoch 15, Loss G: -0.1503,Loss D: -0.0518
Epoch 16, Loss G: -0.2306,Loss D: -0.0234
Epoch 17, Loss G: -0.2986,Loss D:  0.0469
Epoch 18, Loss G: -0.1941,Loss D: -0.0560
Epoch 19, Loss G: -0.3794,Loss D:  0.0000
Epoch 20, Loss G: -0.2763,Loss D:  0.0368
   batsmanIdx  bowlerIdx  ballNum  ballsRemaining  runs   runRate  numWickets  \
0         906        224        8              75    81  1.955153           4   
1        4159        433       17              31   126  1.799280           9   
2         229        351      192              66    82  1.608527           5   
3        1926        962       63               0   117  1.658105           0   
4         286        431      128               1    36  1.605079           0   

   runsMomentum  perfIndex  isWinner  
0      0.146670   6.937595         1  
1      0.160534  10.904346         1  
2      0.516010  11.698128         1  
3      0.380986  11.914613         0  
4      0.112255   5.392120         0  
(30000, 10)
1
Epoch 1, Loss G:  7.9977,Loss D: -0.3592
Epoch 2, Loss G:  3.7418,Loss D: -0.3371
Epoch 3, Loss G:  1.6685,Loss D: -0.3211
Epoch 4, Loss G:  1.0539,Loss D: -0.3495
Epoch 5, Loss G:  0.4664,Loss D: -0.0907
Epoch 6, Loss G:  0.4004,Loss D: -0.1208
Epoch 7, Loss G:  0.3250,Loss D: -0.1482
Epoch 8, Loss G:  0.1753,Loss D:  0.0169
Epoch 9, Loss G:  0.1382,Loss D:  0.0661
Epoch 10, Loss G:  0.1509,Loss D: -0.1023
Epoch 11, Loss G: -0.0235,Loss D:  0.0210
Epoch 12, Loss G: -0.1636,Loss D: -0.0124
Epoch 13, Loss G: -0.3370,Loss D: -0.0185
Epoch 14, Loss G: -0.3054,Loss D: -0.0085
Epoch 15, Loss G: -0.5142,Loss D:  0.0121
Epoch 16, Loss G: -0.3813,Loss D: -0.0921
Epoch 17, Loss G: -0.5838,Loss D:  0.0210
Epoch 18, Loss G: -0.4033,Loss D: -0.0181
Epoch 19, Loss G: -0.5711,Loss D:  0.0269
Epoch 20, Loss G: -0.4828,Loss D: -0.0830
   batsmanIdx  bowlerIdx  ballNum  ballsRemaining  runs   runRate  numWickets  \
0        2202        265      223              39    13  0.868927           0   
1        3641        856       35              59    26  2.236160           6   
2         676       2903      218              93    16  0.460693           1   
3        3482       3459       44             117   102  0.851471           8   
4        3046       3076       59               5    84  1.016824           2   

   runsMomentum  perfIndex  isWinner  
0      0.138586   4.733462         0  
1      0.124453   5.146831         1  
2      0.273168  10.106869         0  
3      0.129520   5.361127         0  
4      1.083525  25.677574         1  
(60000, 10)
...
...
11
Epoch 1, Loss G:  8.8362,Loss D: -0.7111
Epoch 2, Loss G:  4.1322,Loss D: -0.8468
Epoch 3, Loss G:  1.2782,Loss D:  0.1245
Epoch 4, Loss G:  1.1135,Loss D: -0.3588
Epoch 5, Loss G:  0.6033,Loss D: -0.1255
Epoch 6, Loss G:  0.6912,Loss D: -0.1906
Epoch 7, Loss G:  0.3340,Loss D: -0.1048
Epoch 8, Loss G:  0.3515,Loss D: -0.0730
Epoch 9, Loss G:  0.1702,Loss D:  0.0237
Epoch 10, Loss G:  0.1064,Loss D:  0.0632
Epoch 11, Loss G:  0.0884,Loss D: -0.0005
Epoch 12, Loss G:  0.0556,Loss D: -0.0607
Epoch 13, Loss G: -0.0917,Loss D: -0.0223
Epoch 14, Loss G: -0.1492,Loss D:  0.0258
Epoch 15, Loss G: -0.0986,Loss D: -0.0112
Epoch 16, Loss G: -0.1428,Loss D: -0.0060
Epoch 17, Loss G: -0.2225,Loss D: -0.0263
Epoch 18, Loss G: -0.2255,Loss D: -0.0328
Epoch 19, Loss G: -0.3482,Loss D:  0.0277
Epoch 20, Loss G: -0.2667,Loss D: -0.0721
   batsmanIdx  bowlerIdx  ballNum  ballsRemaining  runs   runRate  numWickets  \
0         367       1447      129              27    30  1.242120           2   
1        2481       1528      221               4    10  1.344024           2   
2        1034       3116      132              87   153  1.142750           3   
3        1201       2868      151              60   136  1.091638           1   
4        4327       3291      108              89    22  0.842775           2   

   runsMomentum  perfIndex  isWinner  
0      1.978739   6.393691         1  
1      0.539650   6.783990         0  
2      0.107156  12.154197         0  
3      3.193574  11.992059         0  
4      0.127507  12.210876         0  
(360000, 10)

E. Sample of the Synthetic data

synthetic_data = ctgan.sample(20000)
print(synthetic_data.head(100))

    batsmanIdx  bowlerIdx  ballNum  ballsRemaining  runs    runRate  \
0         1073       3059       72              72   149   2.230236   
1         3769       1443      106               7   137   0.881409   
2          448       3048      166               6   220   1.092504   
3         2969       1244      103              82   207  12.314862   
4          180       1372      125             111    14   1.310051   
..         ...        ...      ...             ...   ...        ...   
95        1521       1040      153               6   166   1.097363   
96        2366         62       25             114   119   0.910642   
97        3506       1736      100             118   140   1.640921   
98        3343       2347       47              54    50   0.696462   
99        1957       2888      136              27   153   1.315565   

    numWickets  runsMomentum  perfIndex  isWinner  
0            0      0.111707  17.466925         0  
1            1      0.130352  14.274113         0  
2            1      0.173541  11.076731         1  
3            1      0.218977   6.239951         0  
4            4      2.829380   9.183323         1  
..         ...           ...        ...       ...  
95           0      0.223437   7.011180         0  
96           1      0.451371  16.908120         1  
97           5      0.156936   9.217205         0  
98           6      0.124536   6.273091         0  
99           1      0.249329  14.221554         0  

[100 rows x 10 columns]

F. Evaluating the synthetic T20 match data

Here the quality of the synthetic data set is evaluated.

a) Statistical evaluation

Read the real T20 match data
Read the generated T20 synthetic match data

import pandas as pd

# Read the T20 match and synthetic match data
df = pd.read_csv('/kaggle/input/cricket1/t20.csv').  #1.2 million rows
synthetic=pd.read_csv('/kaggle/input/synthetic/synthetic.csv')   #300K

# Randomly sample 1000 rows, and generate stats
df1=df.sample(n=1000)
real=df1.describe()
realData_stats=real.transpose
print(realData_stats)

synthetic1=synthetic.sample(n=1000)
synthetic=synthetic1.describe()
syntheticData_stats=synthetic.transpose
syntheticData_stats

a) Stats of real T20 match data

<bound method DataFrame.transpose of         batsmanIdx    bowlerIdx      ballNum  ballsRemaining         runs  \
count  1000.000000  1000.000000  1000.000000     1000.000000  1000.000000   
mean   2323.940000  1776.481000   118.165000       59.236000    77.649000   
std    1329.703046  1011.470703    70.564291       35.312934    49.098763   
min       8.000000    13.000000     1.000000        1.000000    -2.000000   
25%    1134.750000   850.000000    58.000000       28.750000    39.000000   
50%    2265.000000  1781.500000   117.000000       59.000000    72.000000   
75%    3510.000000  2662.250000   178.000000       89.000000   111.000000   
max    4738.000000  3481.000000   265.000000      127.000000   246.000000   

           runRate   numWickets  runsMomentum    perfIndex     isWinner  
count  1000.000000  1000.000000   1000.000000  1000.000000  1000.000000  
mean      1.734979     2.614000      0.310568     9.580386     0.499000  
std       5.698104     2.267189      0.686171     4.530856     0.500249  
min      -2.000000     0.000000      0.071429     0.000000     0.000000  
25%       1.009063     1.000000      0.105769     6.666667     0.000000  
50%       1.272727     2.000000      0.141026     9.236842     0.000000  
75%       1.546891     4.000000      0.250000    12.146735     1.000000  
max     166.000000    10.000000     10.000000    30.800000     1.000000

b) Stats of Synthetic T20 match data

     
           batsmanIdx    bowlerIdx      ballNum  ballsRemaining         runs  \
count  1000.000000  1000.000000  1000.000000     1000.000000  1000.000000   
mean   2304.135000  1760.776000   116.081000       50.102000    74.357000   
std    1342.348684  1003.496003    72.019228       35.795236    48.103446   
min       2.000000    15.000000    -4.000000       -2.000000    -1.000000   
25%    1093.000000   881.000000    46.000000       18.000000    30.000000   
50%    2219.500000  1763.500000   116.000000       45.000000    75.000000   
75%    3496.500000  2644.750000   180.250000       77.000000   112.000000   
max    4718.000000  3481.000000   253.000000      124.000000   222.000000   

           runRate   numWickets  runsMomentum    perfIndex     isWinner  
count  1000.000000  1000.000000   1000.000000  1000.000000  1000.000000  
mean      1.637225     3.096000      0.336540     9.278073     0.507000  
std       1.691060     2.640408      0.502346     4.727677     0.500201  
min      -4.388339     0.000000      0.083351    -0.902991     0.000000  
25%       1.077789     1.000000      0.115770     5.731931     0.000000  
50%       1.369655     2.000000      0.163085     9.104328     1.000000  
75%       1.660477     5.000000      0.311586    12.619318     1.000000  
max      23.757001    10.000000      4.630908    29.829497     1.000000

c) Plotting the Generator and Discriminator loss

import pandas as pd

# CTGAN prints out a new line for each epoch
epochs_output = str(output).split('\n')

# CTGAN separates the values with commas
raw_values = [line.split(',') for line in epochs_output]
loss_values = pd.DataFrame(raw_values)[:-1] # convert to df and delete last row (empty)

# Rename columns
loss_values.columns = ['Epoch', 'Generator Loss', 'Discriminator Loss']

# Extract the numbers from each column 
loss_values['Epoch'] = loss_values['Epoch'].str.extract('(\d+)').astype(int)
loss_values['Generator Loss'] = loss_values['Generator Loss'].str.extract('([-+]?\d*\.\d+|\d+)').astype(float)
loss_values['Discriminator Loss'] = loss_values['Discriminator Loss'].str.extract('([-+]?\d*\.\d+|\d+)').astype(float)

# the result is a row for each epoch that contains the generator and discriminator loss
loss_values.head()

	Epoch	Generator Loss	Discriminator Loss
0	1	8.0158	-0.3840
1	2	4.6748	-0.9589
2	3	1.1503	-0.0066
3	4	1.5593	-0.8148
4	5	0.6734	-0.1425
5	6	0.5342	-0.2202
6	7	0.4539	-0.1462
7	8	0.2907	-0.0155
8	9	0.2399	0.0172
9	10	0.1520	-0.0236

import plotly.graph_objects as go

# Plot loss function
fig = go.Figure(data=[go.Scatter(x=loss_values['Epoch'], y=loss_values['Generator Loss'], name='Generator Loss'),
                      go.Scatter(x=loss_values['Epoch'], y=loss_values['Discriminator Loss'], name='Discriminator Loss')])


# Update the layout for best viewing
fig.update_layout(template='plotly_white',
                    legend_orientation="h",
                    legend=dict(x=0, y=1.1))

title = 'CTGAN loss function for T20 dataset - ' 
fig.update_layout(title=title, xaxis_title='Epoch', yaxis_title='Loss')
fig.show()

G. Qualitative evaluation of Synthetic data

a) Quality of continuous columns in synthetic data

KSComplement -This metric computes the similarity of a real column vs. a synthetic column in terms of the column shapes.The KSComplement uses the Kolmogorov-Smirnov statistic. Closer to 1.0 is good and 0 is worst

from sdmetrics.single_column import KSComplement
numerical_columns=['ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']
total_score = 0
for column_name in numerical_columns:
    column_score = KSComplement.compute(df[column_name], synthetic[column_name])
    total_score += column_score
    print('Column:', column_name, ', Score: ', column_score)

print('\nAverage: ', total_score/len(numerical_columns))

Column: ballNum , Score:  0.9502754283367316
Column: ballsRemaining , Score:  0.8770284103276166
Column: runs , Score:  0.9136464248633367
Column: runRate , Score:  0.9183841670732166
Column: numWickets , Score:  0.9016209114638712
Column: runsMomentum , Score:  0.8773491702213716
Column: perfIndex , Score:  0.9173808852778924

Average:  0.9079550567948624

b) Quality of categorical columns

This statistic measures the quality of generated categorical columns. 1 is best and 0 is worst

categorical_columns=['batsmanIdx','bowlerIdx']
from sdmetrics.single_column import TVComplement

total_score = 0
for column_name in categorical_columns:
    column_score = TVComplement.compute(df[column_name], synthetic[column_name])
    total_score += column_score
    print('Column:', column_name, ', Score: ', column_score)

print('\nAverage: ', total_score/len(categorical_columns))

Column: batsmanIdx , Score:  0.8436263499539245
Column: bowlerIdx , Score:  0.7356177407921669

Average:  0.7896220453730457

The performance is decent but not excellent. I was unable to execute more epochs as it it required larger than the memory allowed

c) Correlation similarity

This metric measures the correlation between a pair of numerical columns and computes the similarity between the real and synthetic data – it compares the trends of 2D distributions. Best 1.0 and 0.0 is worst

import itertools
from sdmetrics.column_pairs import CorrelationSimilarity

total_score = 0
total_pairs = 0
for pair in itertools.combinations(numerical_columns,2):
    col_A, col_B = pair
    score = CorrelationSimilarity.compute(df[[col_A, col_B]], synthetic[[col_A, col_B]])
    print('Columns:', pair, ' Score:', score)
    total_score += score
    total_pairs += 1

print('\nAverage: ', total_score/total_pairs)

Columns: ('ballNum', 'ballsRemaining')  Score: 0.7153942317384889
Columns: ('ballNum', 'runs')  Score: 0.8838043045134777
Columns: ('ballNum', 'runRate')  Score: 0.8710243133637056
Columns: ('ballNum', 'numWickets')  Score: 0.7978515509750435
Columns: ('ballNum', 'runsMomentum')  Score: 0.8956281260834316
Columns: ('ballNum', 'perfIndex')  Score: 0.9275145840528048
Columns: ('ballsRemaining', 'runs')  Score: 0.9566928975064546
Columns: ('ballsRemaining', 'runRate')  Score: 0.9127313819127167
Columns: ('ballsRemaining', 'numWickets')  Score: 0.6770737279315224
Columns: ('ballsRemaining', 'runsMomentum')  Score: 0.7939260278412358
Columns: ('ballsRemaining', 'perfIndex')  Score: 0.8694582252638351
Columns: ('runs', 'runRate')  Score: 0.999593795992159
Columns: ('runs', 'numWickets')  Score: 0.9510731832916608
Columns: ('runs', 'runsMomentum')  Score: 0.9956131422133428
Columns: ('runs', 'perfIndex')  Score: 0.9742931845536701
Columns: ('runRate', 'numWickets')  Score: 0.8859830711832263
Columns: ('runRate', 'runsMomentum')  Score: 0.9174744874779561
Columns: ('runRate', 'perfIndex')  Score: 0.9491100087911353
Columns: ('numWickets', 'runsMomentum')  Score: 0.8989709776329797
Columns: ('numWickets', 'perfIndex')  Score: 0.7178946968801441
Columns: ('runsMomentum', 'perfIndex')  Score: 0.9744441623018661

Average:  0.8840738134048025

d) Category coverage

This metric measures whether a synthetic column covers all the possible categories that are present in a real column. 1.0 is best , 0 is worst

from sdmetrics.single_column import CategoryCoverage

total_score = 0
for column_name in categorical_columns:
    column_score = CategoryCoverage.compute(df[column_name], synthetic[column_name])
    total_score += column_score
    print('Column:', column_name, ', Score: ', column_score)

print('\nAverage: ', total_score/len(categorical_columns))

Column: batsmanIdx , Score:  0.9533951919021509
Column: bowlerIdx , Score:  0.9913966160022942

Average:  0.9723959039522225

H. Augmenting the T20 match data set

In this final part I augment my T20 match data set with the generated synthetic T20 data set.

import pandas as pd
from numpy import savetxt
import tensorflow as tf
from tensorflow import keras
import pandas as pd
import numpy as np


from keras.layers import Input, Embedding, Flatten, Dense, Reshape, Concatenate, Dropout
from keras.models import Model
import matplotlib.pyplot as plt

# Read real and synthetic data
df = pd.read_csv('/kaggle/input/cricket1/t20.csv')
synthetic=pd.read_csv('/kaggle/input/synthetic/synthetic.csv')

# Augment the data. Concatenate real & synthetic data
df1=pd.concat([df,synthetic])

# Create training and test samples
print("Shape of dataframe=",df1.shape)
train_dataset = df1.sample(frac=0.8,random_state=0)
test_dataset = df1.drop(train_dataset.index)
train_dataset1 = train_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_dataset1 = test_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
train_dataset1
train_labels = train_dataset.pop('isWinner')
test_labels = test_dataset.pop('isWinner')
print(train_dataset1.shape)

a=train_dataset1.describe()
stats=a.transpose
print(a)

a) Create A Deep Learning Model in Keras

from numpy.random import seed
seed(33)
tf.random.set_seed(432)
# create input layers for each of the predictors
batsmanIdx_input = Input(shape=(1,), name='batsmanIdx')
bowlerIdx_input = Input(shape=(1,), name='bowlerIdx')
ballNum_input = Input(shape=(1,), name='ballNum')
ballsRemaining_input = Input(shape=(1,), name='ballsRemaining')
runs_input = Input(shape=(1,), name='runs')
runRate_input = Input(shape=(1,), name='runRate')
numWickets_input = Input(shape=(1,), name='numWickets')
runsMomentum_input = Input(shape=(1,), name='runsMomentum')
perfIndex_input = Input(shape=(1,), name='perfIndex')

no_of_unique_batman=len(df1["batsmanIdx"].unique()) 
print(no_of_unique_batman)
no_of_unique_bowler=len(df1["bowlerIdx"].unique()) 
print(no_of_unique_bowler)

embedding_size_bat = no_of_unique_batman ** (1/4)
print(embedding_size_bat)
embedding_size_bwl = no_of_unique_bowler ** (1/4)
print(embedding_size_bwl)

# create embedding layer for the categorical predictor
batsmanIdx_embedding = Embedding(input_dim=no_of_unique_batman+1, output_dim=16,input_length=1)(batsmanIdx_input)
print(batsmanIdx_embedding)
batsmanIdx_flatten = Flatten()(batsmanIdx_embedding)
print(batsmanIdx_flatten)
bowlerIdx_embedding = Embedding(input_dim=no_of_unique_bowler+1, output_dim=16,input_length=1)(bowlerIdx_input)
bowlerIdx_flatten = Flatten()(bowlerIdx_embedding)
print(bowlerIdx_flatten)
# concatenate all the predictors
x = keras.layers.concatenate([batsmanIdx_flatten,bowlerIdx_flatten, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input])
print(x.shape)
# add hidden layers
x = Dense(96, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(64, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(32, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(16, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(8, activation='relu')(x)
x = Dropout(0.1)(x)
# add output layer
output = Dense(1, activation='sigmoid', name='output')(x)
print(output.shape)
# create model
model = Model(inputs=[batsmanIdx_input,bowlerIdx_input, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input], outputs=output)
model.summary()
# compile model
#optimizer=keras.optimizers.Adam(learning_rate=.01, beta_1=0.1, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=True)
#optimizer=keras.optimizers.RMSprop(learning_rate=0.001, rho=0.2, momentum=0.2, epsilon=1e-07)
#optimizer=keras.optimizers.SGD(learning_rate=.01,momentum=0.1) #- Works without dropout
#optimizer = tf.keras.optimizers.RMSprop(0.01)
#optimizer=keras.optimizers.SGD(learning_rate=.01,momentum=0.1)
#optimizer=keras.optimizers.RMSprop(learning_rate=.005, rho=0.1, momentum=0, epsilon=1e-07)

optimizer=keras.optimizers.Adam(learning_rate=.015, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=True)

model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=['accuracy'])

# train the model
history=model.fit([train_dataset1['batsmanIdx'],train_dataset1['bowlerIdx'],train_dataset1['ballNum'],train_dataset1['ballsRemaining'],train_dataset1['runs'],
           train_dataset1['runRate'],train_dataset1['numWickets'],train_dataset1['runsMomentum'],train_dataset1['perfIndex']], train_labels, epochs=20, batch_size=1024,
          validation_data = ([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']],test_labels), verbose=1)

plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train", "test"], loc="upper left")
plt.show()

==================================================================================================
Total params: 144,497
Trainable params: 144,497
Non-trainable params: 0
__________________________________________________________________________________________________
Epoch 1/20
1219/1219 [==============================] - 15s 11ms/step - loss: 0.6285 - accuracy: 0.6372 - val_loss: 0.5164 - val_accuracy: 0.7606
Epoch 2/20
1219/1219 [==============================] - 14s 11ms/step - loss: 0.5594 - accuracy: 0.7121 - val_loss: 0.4920 - val_accuracy: 0.7663
Epoch 3/20
1219/1219 [==============================] - 14s 12ms/step - loss: 0.5338 - accuracy: 0.7244 - val_loss: 0.4541 - val_accuracy: 0.7878
Epoch 4/20
1219/1219 [==============================] - 14s 11ms/step - loss: 0.5176 - accuracy: 0.7317 - val_loss: 0.4226 - val_accuracy: 0.7933
Epoch 5/20
1219/1219 [==============================] - 13s 11ms/step - loss: 0.4966 - accuracy: 0.7420 - val_loss: 0.4547 - val_accuracy: 0.7
...
...
poch 18/20
1219/1219 [==============================] - 14s 11ms/step - loss: 0.4300 - accuracy: 0.7747 - val_loss: 0.3536 - val_accuracy: 0.8288
Epoch 19/20
1219/1219 [==============================] - 14s 12ms/step - loss: 0.4269 - accuracy: 0.7766 - val_loss: 0.3565 - val_accuracy: 0.8302
Epoch 20/20
1219/1219 [==============================] - 14s 11ms/step - loss: 0.4259 - accuracy: 0.7775 - val_loss: 0.3498 - val_accuracy: 0.831

As can be seen the accuracy with augmented dataset is around 0.77, while without it I was getting 0.867 with just the real data. This degradation is probably due to the folllowing reasons

Only a fraction of the dataset was used for training. This was not representative of the data distribution for CTGAN to correctly synthesise data
The number of epochs had to be kept low to prevent Kaggle/Colab from crashing

I. Conclusion

This post shows how we can generate synthetic T20 match data to augment real T20 match data. Assuming we have sufficient processing power we should be able to generate synthetic data for augmenting our data set. This should improve the accuracy of the Win Probabily Deep Learning model.

References

Also see

To see all posts click Index of posts

GooglyPlusPlus: Win Probability using Deep Learning and player embeddings

In my last post ‘GooglyPlusPlus now with Win Probability Analysis for all T20 matches‘ I had discussed the performance of my ML models, created with and without player embeddings, in computing the Win Probability of T20 matches. With batsman & bowler embeddings I got much better performance than without the embeddings

glmnet – Accuracy – 0.73
Random Forest (RF) – Accuracy – 0.92

While the Random Forest gave excellent accuracy, it was bulky and also took an unusually long time to predict the Win Probability of a single T20 match. The above 2 ML models were built using R’s Tidymodels. glmnet was fast, but I wanted to see if I could create a ML model that was better, lighter and faster. I had initially tried to use Tensorflow, Keras in Python but then abandoned it, since I did not know how to port the Deep Learning model to R and use in my app GooglyPlusPlus.

But later, since I was stuck with a bulky Random Forest model, I decided to again explore options for saving the Keras Deep Learning model and loading it in R. I found out that saving the model as .h5, we can load it in R and use it for predictions. Hence, I rebuilt a Deep Learning model using Keras, Python with player embeddings and I got excellent performance. The DL model was light and had an accuracy 0.8639 with an ROC_AUC of 0.964 which was great!

GooglyPlusPlus uses data from Cricsheet and is based on my R package yorkr

You can try out this latest version of GooglyPlusPlus at gpp2023-1

Here are the steps

A. Build a Keras Deep Learning model

a. Import necessary packages

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from pathlib import Path
import matplotlib.pyplot as plt

b, Upload the data of all 9 T20 leagues (BBL, CPL, IPL, T20 (men) , T20(women), NTB, CPL, SSM, WBB)

# Read all T20 leagues 
df1=pd.read_csv('t20.csv')
print("Shape of dataframe=",df1.shape)

# Create training and test data set
train_dataset = df1.sample(frac=0.8,random_state=0)
test_dataset = df1.drop(train_dataset.index)
train_dataset1 = train_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_dataset1 = test_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
train_dataset1

# Set the target data
train_labels = train_dataset.pop('isWinner')
test_labels = test_dataset.pop('isWinner')
train_dataset1

a=train_dataset1.describe()
stats=a.transpose
a

c. Create a Deep Learning ML model using batsman & bowler embeddings

import pandas as pd
import numpy as np
from keras.layers import Input, Embedding, Flatten, Dense
from keras.models import Model
from keras.layers import Input, Embedding, Flatten, Dense, Reshape, Concatenate, Dropout
from keras.models import Model

# Set seed
tf.random.set_seed(432)

# create input layers for each of the predictors
batsmanIdx_input = Input(shape=(1,), name='batsmanIdx')
bowlerIdx_input = Input(shape=(1,), name='bowlerIdx')
ballNum_input = Input(shape=(1,), name='ballNum')
ballsRemaining_input = Input(shape=(1,), name='ballsRemaining')
runs_input = Input(shape=(1,), name='runs')
runRate_input = Input(shape=(1,), name='runRate')
numWickets_input = Input(shape=(1,), name='numWickets')
runsMomentum_input = Input(shape=(1,), name='runsMomentum')
perfIndex_input = Input(shape=(1,), name='perfIndex')

# Set the embedding size as the 4th root of unique batsmen, bowlers
no_of_unique_batman=len(df1["batsmanIdx"].unique()) 
no_of_unique_bowler=len(df1["bowlerIdx"].unique()) 
embedding_size_bat = no_of_unique_batman ** (1/4)
embedding_size_bwl = no_of_unique_bowler ** (1/4)


# create embedding layer for the categorical predictor
batsmanIdx_embedding = Embedding(input_dim=no_of_unique_batman+1, output_dim=16,input_length=1)(batsmanIdx_input)
batsmanIdx_flatten = Flatten()(batsmanIdx_embedding)
bowlerIdx_embedding = Embedding(input_dim=no_of_unique_bowler+1, output_dim=16,input_length=1)(bowlerIdx_input)
bowlerIdx_flatten = Flatten()(bowlerIdx_embedding)

# concatenate all the predictors
x = keras.layers.concatenate([batsmanIdx_flatten,bowlerIdx_flatten, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input])

# add hidden layers
# Use dropouts for regularisation
x = Dense(64, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(32, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(16, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(8, activation='relu')(x)
x = Dropout(0.1)(x)

# add output layer
output = Dense(1, activation='sigmoid', name='output')(x)
print(output.shape)

# create a DL model
model = Model(inputs=[batsmanIdx_input,bowlerIdx_input, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input], outputs=output)
model.summary()

# compile model
optimizer=keras.optimizers.Adam(learning_rate=.01, beta_1=0.9, beta_2=0.999, epsilon=1e-07, decay=0.0, amsgrad=True)

model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=['accuracy'])

# train the model
history=model.fit([train_dataset1['batsmanIdx'],train_dataset1['bowlerIdx'],train_dataset1['ballNum'],train_dataset1['ballsRemaining'],train_dataset1['runs'],
           train_dataset1['runRate'],train_dataset1['numWickets'],train_dataset1['runsMomentum'],train_dataset1['perfIndex']], train_labels, epochs=40, batch_size=1024,
          validation_data = ([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']],test_labels), verbose=1)

plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train", "test"], loc="upper left")
plt.show()

Model: "model_5"
__________________________________________________________________________________________________
 Layer (type)                   Output Shape         Param #     Connected to                     
==================================================================================================
 batsmanIdx (InputLayer)        [(None, 1)]          0           []                               
                                                                                                  
 bowlerIdx (InputLayer)         [(None, 1)]          0           []                               
                                                                                                  
 embedding_10 (Embedding)       (None, 1, 16)        75888       ['batsmanIdx[0][0]']             
                                                                                                  
 embedding_11 (Embedding)       (None, 1, 16)        55808       ['bowlerIdx[0][0]']              
                                                                                                  
 flatten_10 (Flatten)           (None, 16)           0           ['embedding_10[0][0]']           
                                                                                                  
 flatten_11 (Flatten)           (None, 16)           0           ['embedding_11[0][0]']           
                                                                                                  
 ballNum (InputLayer)           [(None, 1)]          0           []                               
                                                                                                  
 ballsRemaining (InputLayer)    [(None, 1)]          0           []                               
                                                                                                  
 runs (InputLayer)              [(None, 1)]          0           []                               
                                                                                                  
 runRate (InputLayer)           [(None, 1)]          0           []                               
                                                                                                  
 numWickets (InputLayer)        [(None, 1)]          0           []                               
                                                                                                  
 runsMomentum (InputLayer)      [(None, 1)]          0           []                               
                                                                                                  
 perfIndex (InputLayer)         [(None, 1)]          0           []                               
                                                                                                  
 concatenate_5 (Concatenate)    (None, 39)           0           ['flatten_10[0][0]',             
                                                                  'flatten_11[0][0]',             
                                                                  'ballNum[0][0]',                
                                                                  'ballsRemaining[0][0]',         
                                                                  'runs[0][0]',                   
                                                                  'runRate[0][0]',                
                                                                  'numWickets[0][0]',             
                                                                  'runsMomentum[0][0]',           
                                                                  'perfIndex[0][0]']              
                                                                                                  
 dense_19 (Dense)               (None, 64)           2560        ['concatenate_5[0][0]']          
                                                                                                  
 dropout_19 (Dropout)           (None, 64)           0           ['dense_19[0][0]']               
                                                                                                  
 dense_20 (Dense)               (None, 32)           2080        ['dropout_19[0][0]']             
                                                                                                  
 dropout_20 (Dropout)           (None, 32)           0           ['dense_20[0][0]']               
                                                                                                  
 dense_21 (Dense)               (None, 16)           528         ['dropout_20[0][0]']             
                                                                                                  
 dropout_21 (Dropout)           (None, 16)           0           ['dense_21[0][0]']               
                                                                                                  
 dense_22 (Dense)               (None, 8)            136         ['dropout_21[0][0]']             
                                                                                                  
 dropout_22 (Dropout)           (None, 8)            0           ['dense_22[0][0]']               
                                                                                                  
 output (Dense)                 (None, 1)            9           ['dropout_22[0][0]']             
                                                                                                  
==================================================================================================
Total params: 137,009
Trainable params: 137,009
Non-trainable params: 0
__________________________________________________________________________________________________
Epoch 1/40
937/937 [==============================] - 11s 10ms/step - loss: 0.5683 - accuracy: 0.6968 - val_loss: 0.4480 - val_accuracy: 0.7708
Epoch 2/40
937/937 [==============================] - 9s 10ms/step - loss: 0.4477 - accuracy: 0.7721 - val_loss: 0.4305 - val_accuracy: 0.7833
Epoch 3/40
937/937 [==============================] - 9s 10ms/step - loss: 0.4229 - accuracy: 0.7832 - val_loss: 0.3984 - val_accuracy: 0.7936
...
...
937/937 [==============================] - 10s 10ms/step - loss: 0.2909 - accuracy: 0.8627 - val_loss: 0.2943 - val_accuracy: 0.8613
Epoch 38/40
937/937 [==============================] - 10s 10ms/step - loss: 0.2892 - accuracy: 0.8633 - val_loss: 0.2933 - val_accuracy: 0.8621
Epoch 39/40
937/937 [==============================] - 10s 10ms/step - loss: 0.2889 - accuracy: 0.8638 - val_loss: 0.2941 - val_accuracy: 0.8620
Epoch 40/40
937/937 [==============================] - 10s 11ms/step - loss: 0.2886 - accuracy: 0.8639 - val_loss: 0.2929 - val_accuracy: 0.8621

d. Compute and plot the ROC-AUC for the above model

from sklearn.metrics import roc_curve

# Select a random sample set
tf.random.set_seed(59)
train = df1.sample(frac=0.9,random_state=0)
test = df1.drop(train_dataset.index)
test_dataset1 = test[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_labels = test.pop('isWinner')

# Compute the predicted values
y_pred_keras = model.predict([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']]).ravel()

# Compute TPR & FPR
fpr_keras, tpr_keras, thresholds_keras = roc_curve(test_labels, y_pred_keras)

fpr_keras, tpr_keras, thresholds_keras = roc_curve(test_labels, y_pred_keras)
from sklearn.metrics import auc

# Plot the Area Under the Curve (AUC)
auc_keras = auc(fpr_keras, tpr_keras)
plt.figure(1)
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_keras, tpr_keras, label='Keras (area = {:.3f})'.format(auc_keras))
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()

The ROC_AUC for the Deep Learning Model is 0.946 as seen below

e. Save the Keras model for use in Python

from keras.models import Model
model.save("wpDL.h5")

f. Load the model in R using rhdf5 package for use in GooglyPlusPlus

library(rhdf5)
dl_model <- load_model_hdf5('wpDL.h5')

This was a huge success for me to be able to create the Deep Learning model in Python and use it in my Shiny app GooglyPlusPlus. The Deep Learning Keras model is light-weight and extremely fast.

The Deep Learning model has now been integrated into GooglyPlusPlus. Now you can check the Win Probability using both a) glmnet (Logistic Regression with lasso regularisation) b) Keras Deep Learning model with dropouts as regularisation

In addition I have created 2 features based on Win Probability (WP)

i) Win Probability (Side-by-side – Plot(interactive) : With this functionality the 1st and 2nd innings will be side-by-side. When the 1st innings is played by team 1, the Win Probability of team 2 = 100 – WP (team1). Similarly, when the 2nd innings is being played by team 2, the Win Probability of team1 = 100 – WP (team 2)

ii) Win Probability (Overlapping) – Plot (static): With this functionality the Win Probabilities of both team1(1st innings) & team 2 (2nd innings) are displayed overlapping, so that we can see how the probabilities vary ball-by-ball.

Note: Since the same UI is used for all match functions I had to re-use the Plot(interactive) and Plot(static) radio buttons for Win Probability (Side-by-side) and Win Probability(Overlapping) respectively

Here are screenshots using both ML models with both functionality for some random matches

B) ICC T20 Men World Cup – Netherland-South Africa- 2022-11-06

i) Match Worm wicket chart

ii) Win Probability with LR (Side-by-Side- Plot(interactive))

iii) Win Probability LR (Overlapping- Plot(static))

iv) Win Probability Deep Learning (Side-by-side – Plot(interactive)

In the 213th ball of the innings South Africa was slightly ahead of Netherlands. After that they crashed and burned!

v) Win Probability Deep Learning (Overlapping – Plot (static)

It can be seen that in the 94th ball of both innings South Africa was ahead of Netherlands before the eventual slump.

C) Intl. T20 (Women) India – New Zealand – 2020 – 02 – 27

Here is an interesting match between India and New Zealand T20 Women’s teams. NZ successfully chased the India’s total in a wildly swinging fortunes. See the charts below

i) Match Worm Wicket chart

ii) Win Probability with LR (Side-by-side – Plot (interactive)

iii) Win Probability with LR (Overlapping – Plot (static)

iv) Win Probability with DL model (Side-by-side – Plot (interactive))

v) Win Probability with DL model (Overlapping – Plot (static))

The above functionality in plotting the Win Probability using LR or DL with both options (Side-by-side or Overlapping) is available for all 9 T20 leagues currently supported by GooglyPlusPlus.

Go ahead and give gpp2023-1 a try!!!

Do also check out my other posts’

To see all posts click Index of posts

Computing Win-Probability of T20 matches

I am late to the ‘Win probability’ computation for T20 matches, but managed to jump on to this bus with this post. Win Probability analysis and computation have been around for some time and are used in baseball, NFL, soccer hockey and others. On T20 cricket, the following posts from White Ball Analytics & Sports Data Science were good pointers to the general approach. The data for the Win Probability computation is taken from Cricsheet.

My initial Machine Learning models could not do better than 62% accuracy. I created a data set of ~830 IPL matches which roughly came to about 280,000 rows of ball-by-ball match data but I could not move beyond 62%. Addition of T20 men moved the needle to 64% accuracy. I spent time tuning Deep Learning networks using Tensorflow and Keras. Finally, I added T20 data from 9 T20 leagues – IPL, T20 men, T20 women, BBL, CPL, NTB, PSL, WBB, SSM. I had one large data set of 1.2 million rows of ball by ball data. The data frame looks like

I created a data frame for each match from ball Num 1 to ballNum ~240 for the 1st and 2nd innings of the match. My initial set of features were ballNum, runs, runRate, numWickets. The target variable isWinner= {0,1} depending on whether the team has won or lost the match.

The features

ballNum – ball number for 1 ~ 240+ in data frame. 1 – 120+ for 1st innings and 120+ – 240+ in 2nd innings including noballs, wides etc.
runs = cumulative runs scored at the ball count
runRate = cumulative runs scored/ ballNum (for 1st innings) and runs= required runs/ball Num for 2nd innings
numWickets = wickets lost

The target variable isWinner can take values {0,1} depending whether the team won or lost

With this initial dataframe, even though I had close to 1.2 million rows of ball by ball data of T20 matches my best performance with vanilla Logistic regression & SVM in Python was about 64% accuracy.

# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB
df1=pd.read_csv('matchesT20M.csv')
df2=pd.read_csv('matchesIPL.csv')
df3=pd.read_csv('matchesBBL.csv')
df4=pd.read_csv('matchesCPL.csv')
df5=pd.read_csv('matchesNTB.csv')
df6=pd.read_csv('matchesPSL.csv')
df7=pd.read_csv('matchesSSM.csv')
df8=pd.read_csv('matchesT20W.csv')
df9=pd.read_csv('matchesWBB.csv')

# Create one large dataframe
df10=pd.concat([df1,df2,df3,df4,df5,df6,df7,df8,df9])
print("Shape of dataframe=",df10.shape)
print("#####################################")
stats=check_values(df10)
print("#####################################")
model_fit(df10)
#norm_model_fit(df,stats)
svm_model_fit(df10)

Shape of dataframe= (1206901, 6)
#####################################
Null values: False
It contains 0 infinite values

Accuracy of Logistic regression classifier on training set: 0.63
Accuracy of Logistic regression classifier on test set: 0.64
Accuracy: 0.64
Precision: 0.62
Recall: 0.65
F1: 0.64


Accuracy of Linear SVC classifier on training set: 0.52
Accuracy of Linear SVC classifier on test set: 0.52

With Tensorflow/Keras the performance was about 67%. I tried several things

Normalisation
Tried different learning rates
Different optimisers – SGD, RMSProp, Adam
Changed depth and width of Neural Network

However I did not get much improvement. Finally I decided to do some Feature engineering. I added 2 new features

a) Runs Momentum : This feature is based on the fact that more the wickets in hand, the more freely the batsmen can make risky strokes, hence increasing the momentum of the runs, This is calculated as

runsMomentum = (11 – numWickets)/balls remaining

b) Performance Index: This feature is the product of the run rate x wickets in hand. In other words, if the strike rate is good and fewer wickets lost at the point in the match, then the performance index is higher at that point in the match will be higher

The final set of features chosen were as below

I had also included the balls Remaining in the innings. Now with this set of features I decided to execute Tensorflow/Keras and do a GridSearch with different learning rates, optimisers. After a couple of hours of computation I got an accuracy of 0.73. I needed to be able to read the ML model in R which required installation of Tensorflow, reticulate and Keras in RStudio and I had several issues. Since I hit a roadblock I moved to regular R models

I performed WIn Probability computation in the following ways

A) Win Probability with Vanilla Logistic Regression (R)

With vanilla Logistic Regression in R using the ‘glm’ package I got an accuracy of 0.67, sensitivity of 0.68 and specificity of 0.65 as shown below

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)

# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB
df1=read.csv("output2/matchesBBL2.csv")
df2=read.csv("output2/matchesCPL2.csv")
df3=read.csv("output2/matchesIPL2.csv")
df4=read.csv("output2/matchesNTB2.csv")
df5=read.csv("output2/matchesPSL2.csv")
df6=read.csv("output2/matchesSSM2.csv")
df7=read.csv("output2/matchesT20M2.csv")
df8=read.csv("output2/matchesT20W2.csv")
df9=read.csv("output2/matchesWBB2.csv")

# Create one large dataframe
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)

# Helper function to split into training/test
trainTestSplit <- function(df,trainPercent,seed1){
  ## Sample size percent
  samp_size <- floor(trainPercent/100 * nrow(df))
  ## set the seed 
  set.seed(seed1)
  idx <- sample(seq_len(nrow(df)), size = samp_size)
  idx
  
}

train_idx <- trainTestSplit(df,trainPercent=80,seed=5)
train <- df[train_idx, ]

test <- df[-train_idx, ]
# Fit a generalized linear logistic model, 
fit=glm(isWinner~.,family=binomial,data=train,control = list(maxit = 50))

a=predict(fit,newdata=train,type="response")
# Set response >0.5 as 1 and <=0.5 as 0
b=as.factor(ifelse(a>0.5,1,0))
# Compute the confusion matrix for training data

confusionMatrix(
  factor(b, levels = 0:1),
  factor(train$isWinner, levels = 0:1)
)

Confusion Matrix and Statistics

          Reference
Prediction    
  0      1
         0 339938 160336
         1 154236 310217
                                         
               Accuracy : 0.6739         
                 95% CI : (0.673, 0.6749)
    No Information Rate : 0.5122         
    P-Value [Acc > NIR] : < 2.2e-16      
                                         
                  Kappa : 0.3473         
                                         
 Mcnemar's Test P-Value : < 2.2e-16      
                                         
            Sensitivity : 0.6879         
            Specificity : 0.6593         
         Pos Pred Value : 0.6795         
         Neg Pred Value : 0.6679         
             Prevalence : 0.5122         
         Detection Rate : 0.3524         
   Detection Prevalence : 0.5186         
      Balanced Accuracy : 0.6736         
                                         
       'Positive' Class : 0      

# This can be saved and loaded as    
saveRDS(fit, "glm.rds")
ml_model <- readRDS("glm.rds")

Using the above ML model on Deccan Chargers vs Chennai Super on 27-04-2009 the Win Probability as the match progresses is as below

The Worm wicket graph of this match shows it was a closely fought match

B) Win Probability using Random Forests with Tidy Models – R

Initially I tried Tidy models with tuning for glmnet. The best I got was 0.67. However, I got an excellent performance using TidyModels with Random Forests. I am using Tidy Models for the first time and I have been blown away with how logically it is constructed, much like dplyr & ggplot2.

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)
library(tidymodels)  

# Helper packages
library(readr)       # for importing data
library(vip) 
library(ranger)
# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB

df1=read.csv("output2/matchesBBL2.csv")
df2=read.csv("output2/matchesCPL2.csv")
df3=read.csv("output2/matchesIPL2.csv")
df4=read.csv("output2/matchesNTB2.csv")
df5=read.csv("output2/matchesPSL2.csv")
df6=read.csv("output2/matchesSSM2.csv")
df7=read.csv("output2/matchesT20M2.csv")
df8=read.csv("output2/matchesT20W2.csv")
df9=read.csv("output2/matchesWBB2.csv")

# Create one large dataframe
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)

dim(df)
[1] 
1205909       8

# Take a peek at the dataset
glimpse(df)
$ ballNum        <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28…
$ ballsRemaining <int> 125, 124, 123, 122, 121, 120, 119, 118, 117, 116, 115, 114, 113, 112, 111, 110, 109, 108, 107, 106, 1…
$ runs           <int> 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 13, 14, 16, 18, 18, 18, 24, 24, 24, 26, 26, 32, 32, 33, 34, 34, 3…
$ runRate        <dbl> 1.0000000, 0.5000000, 0.6666667, 0.7500000, 0.6000000, 0.5000000, 0.5714286, 0.5000000, 0.5555556, 0.…
$ numWickets     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3,…
$ runsMomentum   <dbl> 0.08800000, 0.08870968, 0.08943089, 0.09016393, 0.09090909, 0.09166667, 0.09243697, 0.09322034, 0.094…
$ perfIndex      <dbl> 11.000000, 5.500000, 7.333333, 8.250000, 6.600000, 5.500000, 6.285714, 5.500000, 6.111111, 5.000000, …
$ isWinner       <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…

df %>% 
  count(isWinner) %>% 
  mutate(prop = n/sum(n))

set.seed(123)
df$isWinner = as.factor(df$isWinner)

# Split the data into training and test set in 80%:20%
splits      <- initial_split(df,prop = 0.80)
df_other <- training(splits)
df_test  <- testing(splits)

# Create a validation set from training set in 80%:20%
set.seed(234)
val_set <- validation_split(df_other, 
                            prop = 0.80)
val_set

# Setup for Random forest using Ranger for classification
# Set up cores for parallel execution
cores <- parallel::detectCores()
cores

#Set up Random Forest engine
rf_mod <- 
  rand_forest(mtry = tune(), min_n = tune(), trees = 1000) %>% 
  set_engine("ranger", num.threads = cores) %>% 
  set_mode("classification")

rf_mod
# The Random Forest engine includes mtry which is number of predictor 
# variables required at each decision  tree with min_n the minimum number # of 
Random Forest Model Specification (classification)

Main Arguments:
  mtry = tune()
  trees = 1000
  min_n = tune()

Engine-Specific Arguments:
  num.threads = cores

Computational engine: ranger


# Setup the predictors and target variable
# Normalise all predictors. Random Forest don't need normalization but
# I have done it anyway
rf_recipe <-
  recipe(isWinner ~ ., data = df_other) %>% 
  step_normalize(all_predictors())

# Create workflow adding the ML model and recipe
rf_workflow <- 
  workflow() %>% 
  add_model(rf_mod) %>% 
  add_recipe(rf_recipe)

# The tune is done for 5 different values of the tuning parameters.
# Metrics include accuracy and roc_auc
rf_res <- 
  rf_workflow %>% 
  tune_grid(val_set,
            grid = 5,
            control = control_grid(save_pred = TRUE),
            metrics = metric_set(accuracy,roc_auc))

$ Pick the best of ROC/AUC
rf_res %>% 
  show_best(metric = "roc_auc")

We can see that when mtry (number of predictors) is 5 or 7 the ROC_AUC is 0.834 which is quite good

# A tibble: 5 × 8
   mtry min_n .metric .estimator  mean     n std_err .config             
  <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1     5    26 roc_auc binary     0.834     1      NA Preprocessor1_Model5
2     7    36 roc_auc binary     0.834     1      NA Preprocessor1_Model3
3     2    17 roc_auc binary     0.833     1      NA Preprocessor1_Model4
4     1    20 roc_auc binary     0.832     1      NA Preprocessor1_Model2
5     5     6 roc_auc binary     0.825     1      NA Preprocessor1_Model1


# Select the model with highest accuracy
rf_res %>% 
  show_best(metric = "accuracy")
   mtry min_n .metric  .estimator  mean     n std_err .config             
  <int> <int> <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1     7    36 accuracy binary     0.737     1      NA Preprocessor1_Model3
2     5    26 accuracy binary     0.736     1      NA Preprocessor1_Model5
3     1    20 accuracy binary     0.736     1      NA Preprocessor1_Model2
4     2    17 accuracy binary     0.735     1      NA Preprocessor1_Model4
5     5     6 accuracy binary     0.731     1      NA Preprocessor1_Model1

# The model with mtry (number of predictors) is 7 has the best accuracy. 
# Hence the best model has mtry=7 and min_n=36

rf_best <- 
  rf_res %>% 
  select_best(metric = "accuracy")

# Display the best model
rf_best
# A tibble: 1 × 3
   mtry min_n .config             
  <int> <int> <chr>               
1     7    36 Preprocessor1_Model3


rf_res %>% 
  collect_predictions()
   id         .pred_class  .row  mtry min_n .pred_0  .pred_1 isWinner .config             
   <chr>      <fct>       <int> <int> <int>   <dbl>    <dbl> <fct>    <chr>               
 1 validation 1               1     5     6 0.497   0.503    0        Preprocessor1_Model1
 2 validation 1               9     5     6 0.00753 0.992    1        Preprocessor1_Model1
 3 validation 0              10     5     6 0.627   0.373    0        Preprocessor1_Model1
 4 validation 0              16     5     6 0.998   0.002    0        Preprocessor1_Model1
 5 validation 1              18     5     6 0.270   0.730    1        Preprocessor1_Model1
 6 validation 0              23     5     6 0.899   0.101    0        Preprocessor1_Model1
 7 validation 1              26     5     6 0.452   0.548    1        Preprocessor1_Model1
 8 validation 0              30     5     6 0.657   0.343    1        Preprocessor1_Model1
 9 validation 0              34     5     6 0.576   0.424    0        Preprocessor1_Model1
10 validation 0              35     5     6 1.00    0.000167 0        Preprocessor1_Model1

rf_auc <- 
  rf_res %>% 
  collect_predictions(parameters = rf_best) %>% 
  roc_curve(isWinner, .pred_0) %>% 
  mutate(model = "Random Forest")

autoplot(rf_auc)

The Final Model

# Create the final Random Forest model with mtry=7 and min_n=36
# engine as "ranger" for classification
last_rf_mod <- 
  rand_forest(mtry = 7, min_n = 36, trees = 1000) %>% 
  set_engine("ranger", num.threads = cores, importance = "impurity") %>% 
  set_mode("classification")


# the last workflow is updated with the final model
last_rf_workflow <- 
  rf_workflow %>% 
  update_model(last_rf_mod)

set.seed(345)
last_rf_fit <- 
  last_rf_workflow %>% 
  last_fit(splits)

# Collect metrics
last_rf_fit %>% 
  collect_metrics()
  .metric  .estimator .estimate .config             
  <chr>    <chr>          <dbl> <chr>               
1 accuracy binary         0.739 Preprocessor1_Model1
2 roc_auc  binary         0.837 Preprocessor1_Model1

The Random Forest model gives an accuracy of 0.739 and ROC_AUC of .837 which I think is quite good. This is roughly what I got with Tensorflow/Keras

# Get the feature importance 
last_rf_fit %>% 
  extract_fit_parsnip() %>% 
  vip(num_features = 7)

Interestingly the feature that I engineered seems to have the maximum importancce namely Performance Index which is a product of Run rate x Wicket in Hand. I would have thought numWickets would be important but in T20 match probably is is not.

 generate predictions from the test set
test_predictions <- last_rf_fit %>% collect_predictions()
> test_predictions
# A tibble: 241,182 × 7
id               .pred_0 .pred_1  .row .pred_class isWinner .config             
<chr>              <dbl>   <dbl> <int> <fct>       <fct>    <chr>               
  1 train/test split   0.496   0.504     1 1           0        Preprocessor1_Model1
2 train/test split   0.640   0.360    11 0           0        Preprocessor1_Model1
3 train/test split   0.596   0.404    14 0           0        Preprocessor1_Model1
4 train/test split   0.287   0.713    22 1           0        Preprocessor1_Model1
5 train/test split   0.616   0.384    28 0           0        Preprocessor1_Model1
6 train/test split   0.516   0.484    36 0           0        Preprocessor1_Model1
7 train/test split   0.754   0.246    37 0           0        Preprocessor1_Model1
8 train/test split   0.641   0.359    39 0           0        Preprocessor1_Model1
9 train/test split   0.811   0.189    40 0           0        Preprocessor1_Model1
10 train/test split   0.618   0.382    42 0           0        Preprocessor1_Model1


# generate a confusion matrix
test_predictions %>% 
  conf_mat(truth = isWinner, estimate = .pred_class)

          Truth
Prediction     0     1
         0 92173 31623
         1 31320 86066

# Create the final model on the train/test data
final_model <- fit(last_rf_workflow, df_other)

# Final model
final_model
══ Workflow [trained] ════════════════════════════════════════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: rand_forest()

── Preprocessor ──────────────────────────────────────────────────────────────────────────────────────────────────────────────
1 Recipe Step

• step_normalize()

── Model ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Ranger result

Call:
 ranger::ranger(x = maybe_data_frame(x), y = y, mtry = min_cols(~7,      x), num.trees = ~1000, min.node.size = min_rows(~36, x),      num.threads = ~cores, importance = ~"impurity", verbose = FALSE,      seed = sample.int(10^5, 1), probability = TRUE) 

Type:                             Probability estimation 
Number of trees:                  1000 
Sample size:                      964727 
Number of independent variables:  7 
Mtry:                             7 
Target node size:                 36 
Variable importance mode:         impurity 
Splitrule:                        gini 
OOB prediction error (Brier s.):  0.1631303

The Random Forest Model’s performance has been quite impressive and probably requires further exploration.

# Saving and loading the model
save(final_model, file = "fit.rda")
load("fit.rda")

#Predicting the Win Probability of CSK vs DD match on 12 May 2012

Comparing this with the Worm wicket graph of this match we see that DD had no chance at all

C) Win Probability with Tensorflow/Keras with Grid Search – Python

I spent a fair amount of time tuning the hyper parameters of the Keras Deep Learning Network. Finally did go for the Grid Search. Incidentally I did ask ChatGPT to suggest code snippets for GridSearch which it promptly did!!!

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from sklearn.model_selection import GridSearchCV

# Define the model
def create_model(optimizer='adam'):
    tf.random.set_seed(4)
    model = tf.keras.Sequential([
        keras.layers.Dense(32, activation=tf.nn.relu, input_shape=[len(train_dataset1.keys())]),
        keras.layers.Dense(16, activation=tf.nn.relu),
        keras.layers.Dense(8, activation=tf.nn.relu),
        keras.layers.Dense(1,activation=tf.nn.sigmoid)
    ])

    # Since this is binary classification use binary_crossentropy
    model.compile(loss='binary_crossentropy',
                    optimizer=optimizer,
                    metrics='accuracy')
    return(model)

    # Create a KerasClassifier object
model = keras.wrappers.scikit_learn.KerasClassifier(build_fn=create_model)

# Define the grid of hyperparameters to search over
batch_size = [1024]
epochs = [40]
learning_rate = [0.01, 0.001, 0.0001]
optimizer = ['SGD', 'RMSprop', 'Adagrad', 'Adadelta', 'Adam', 'Adamax', 'Nadam']

param_grid = dict(dict(optimizer=optimizer,batch_size=batch_size, epochs=epochs) )
# Create the grid search object
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=3)

# Fit the grid search object to the training data
grid_search.fit(normalized_train_data, train_labels)

# Print the best hyperparameters
print('Best hyperparameters:', grid_search.best_params_)
# summarize results
print("Best: %f using %s" % (grid_search.best_score_, grid_search.best_params_))
means = grid_search.cv_results_['mean_test_score']
stds = grid_search.cv_results_['std_test_score']
params = grid_search.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

The best worked out to be the optimiser ‘Nadam’ with a learning rate of 0.001

import matplotlib.pyplot as plt
# Create a model
tf.random.set_seed(4)
model = tf.keras.Sequential([
    keras.layers.Dense(32, activation=tf.nn.relu, input_shape=[len(train_dataset1.keys())]),
    keras.layers.Dense(16, activation=tf.nn.relu),
    keras.layers.Dense(8, activation=tf.nn.relu),
    keras.layers.Dense(1,activation=tf.nn.sigmoid)
  ])

# Use the Nadam optimiser
optimizer=keras.optimizers.Nadam(learning_rate=.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, decay=0.0)

# Since this is binary classification use binary_crossentropy
model.compile(loss='binary_crossentropy',
                optimizer=optimizer,
                metrics='accuracy')

# Fit 
#history=model.fit(
#  train_dataset1, train_labels,batch_size=1024,
#  epochs=40, validation_data=(test_dataset1,test_labels), verbose=1)
history=model.fit(
  normalized_train_data, train_labels,batch_size=1024,
  epochs=40, validation_data=(normalized_test_data,test_labels), verbose=1)

Epoch 37/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4971 - accuracy: 0.7310 - val_loss: 0.4968 - val_accuracy: 0.7357
Epoch 38/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4970 - accuracy: 0.7310 - val_loss: 0.4974 - val_accuracy: 0.7378
Epoch 39/40
943/943 [==============================] - 4s 4ms/step - loss: 0.4970 - accuracy: 0.7309 - val_loss: 0.4994 - val_accuracy: 0.7296
Epoch 40/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4969 - accuracy: 0.7311 - val_loss: 0.4998 - val_accuracy: 0.7300
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train", "test"], loc="upper left")
plt.show()

Conclusion

So, the Keras Deep Learning Network gives about the same performance of Random Forest in Tidy Models. But I went with R Random Forest as it was easier to save and load the model for use with my data. Also, I am not sure whether the performance of the ML model can be improved beyond a point. However, I will continue to explore.

Watch this space!!!

Also see

To see all posts click Index of posts

References

Using embeddings, collaborative filtering with Deep Learning to analyse T20 players

There is a school of thought which considers that total runs scored and strike rate for a batsman, or total wickets taken and economy rate for a bowler, do not tell the whole story. This is true to a fair extent. The runs scored or the wickets taken could have been against weaker teams and hence the runs, strike rate or the wickets and economy rate alone do not capture all the performance details of the batsman or bowler. A technique to determine the performance of batsmen against different bowlers and identify the batsman’s possible performance even against bowlers he/she has not yet faced could be done with collaborative filtering. Collaborative filtering, with embeddings can also be used to group players with similar characteristics. Similarly, we could also identify the performance of bowlers versus different batsmen. Hence we need to look at average runs, SR and total wickets, ER with the lens of batsmen, bowlers against similar opposition. This is where collaborative filtering is useful.

The table below shows the performance of all batsman against all bowlers in the table below. The row in the table below is the batsman and the column is the bowler, with the value in the cell is the total Runs scored by the batsman against the bowler in all matches. Note the values are 0 for batsmen who have not yet faced specific bowlers. The table is fairly sparse.

Table A

Similarly, we can compute the performance of all bowlers against all batsmen as in the table below. Here the row is the bowler, the column batsman and the value in the cell is the number of times the bowler got the batsman’s wicket. As before the data is sparsely populated

This problem of computing batsman’s performance against bowlers or vice versa, is identical to the user vs movie rating problem used in collaborative filtering. For e.g we could consider

This above problem depicted could be computed using collaborative filtering with embeddings. We could assign sequential numbers for the batsmen from 1 to M, and for the bowlers from 1 to N. The total runs scored could be represented only for the rows where there are values. One way to solve this problem in Machine Learning is to use One Hot Encoding (OHE), where we assign values for each row and each column and map the values of the table with values of the cell for each combination. But this would take a enormous computation time and memory. The solution to this is use vector embeddings. Here embeddings could be used for capturing the sparse tensors between the batsmen, bowlers, runs scored or vice versa between bowlers against batsmen and the wickets taken. We only need to consider the cells for which values exist. An embedding is a relatively low-dimensional space, into which you can translate high-dimensional vectors. An embedding captures some of the semantics of the input by placing semantically similar inputs close together in the embedding space.

a) To compute bowler performances and identify similarities between bowlers the following embedding in the Deep Learning Network was used

To compute batsmen similarities a similar Deep Learning network for bowler vs batsmen is used

I had earlier created another post Player Performance Estimation using AI Collaborative Filtering for batsman and bowler recommendation, using R package Recommender Lab. However, I was not too happy with the results I got with this R package. When I searched the net for material on using embeddings for collaborative filtering, most of material on the web on movie lens or word2vec are repetitive and have no new material. Finally, this short video lecture from Developer Google on Embeddings provided the most clarity.

I have created 4 Colab notebooks to identify player similarities (recommendations)

a) Batsman similarities IPL

b) Batsman similarities T20

c) Bowler similarities IPL

d) Bowler similarities T20

For creating the model I have used all the data for T20 and IPL from so that I get the best results. The data is from Cricsheet. I have also used Google’s Embeddings Projector to display batsman and bowler embedding to and to group similar players

All the Colab notebooks and the data associated with the code are available in Github. Feel free to download and execute them. See if you get better performance. I tried a wide variety of hyperparameters – learning rate, width and depth of nodes per layer, number of layers, gradient methods etc.

You can download all the code & data from Github at embeddings

A) Batsman Recommender IPL (BatsmanRecommenderIPLA.ipynb)

Steps for creating the model

a) Upload bowler vs batsmen with times wicket was taken for batsman. This will be a sparse matrix

b) Assign integer indices for bowlers, batsmen

c) Add additional input features balls, runs conceded and Economy rate

d) Minimise loss for wickets taken for the bowler using SGD

e) Display embeddings of similar batsmen using Tensorboard projector

a) Upload data

Upload data file
2. Remove rows where wickets = 0

from google.colab import files
import io
uploaded = files.upload()
df2 = pd.read_csv(io.BytesIO(uploaded['bowlerVsBatsmanIPLE.csv']))
print(df2.shape)
df2 = df2.loc[df2['wicketTaken']!= 0]
print(df2.shape)

uploaded = files.upload()
df6 = pd.read_csv(io.BytesIO(uploaded['bowlerVsBatsmanIPLAll.csv']))
df6

Out[14]:

	bowler1	batsman1	balls	runsConceded	ER
0	A Ashish Reddy	DJG Sammy	1	0	0.000000
1	A Ashish Reddy	G Gambhir	10	17	10.200000
2	A Ashish Reddy	JEC Franklin	2	0	0.000000
3	A Ashish Reddy	LRPL Taylor	5	6	7.200000
4	A Ashish Reddy	MA Agarwal	3	7	14.000000
…	…	…	…	…	…
8550	Z Khan	Vishnu Vinod	4	8	12.000000
8551	Z Khan	VS Malik	3	5	10.000000
8552	Z Khan	W Jaffer	7	3	2.571429
8553	Z Khan	YK Pathan	22	35	9.545455
8554	Z Khan	Yuvraj Singh	12	12	6.000000

b) Create integer dictionaries for batsmen & bowlers

bowlers = df3["bowler1"].unique().tolist()
bowlers
# Create dictionary of bowler to index
bowlers2index = {x: i for i, x in enumerate(bowlers)}
bowlers2index
#Create dictionary of index tp bowler
index2bowlers = {i: x for i, x in enumerate(bowlers)}
index2bowlers


batsmen = df3["batsman1"].unique().tolist()
batsmen
# Create dictionary of batsman to index
batsmen2index = {x: i for i, x in enumerate(batsmen)}
batsmen2index
# Create dictionary of index to batsman
index2batsmen = {i: x for i, x in enumerate(batsmen)}
index2batsmen

#Map bowler, batsman to respective indices
df3["bowler"] = df3["bowler1"].map(bowlers2index)
df3["batsman"] = df3["batsman1"].map(batsmen2index)
df3
num_bowlers =len(bowlers2index)
num_batsmen = len(batsmen2index)
df3["wicketTaken"] = df3["wicketTaken"].values.astype(np.float32)
df3
# min and max ratings will be used to normalize the ratings later
min_wicketTaken = min(df3["wicketTaken"])
max_wicketTaken = max(df3["wicketTaken"])

print(
    "Number of bowlers: {}, Number of batsmen: {}, Min wicketsTaken: {}, Max wicketsTaken: {}".format(
        num_bowlers, num_batsmen, min_wicketTaken, max_wicketTaken
    )
)

c) Concatenate additional features

df3
df6
df31=pd.concat([df3,df6],axis=1)
df31

d) Create a Tensorflow/Keras deep learning mode. Minimise using Mean Squared Error using Stochastic Gradient Descent. I used ‘dropouts’ to regularise the model to keep validation loss within limits

tf.random.set_seed(4)
vector_size=len(batsmen2index)

df4=df31[['bowler','batsman','wicketTaken','balls','runsConceded','ER']]
df4
train_dataset = df4.sample(frac=0.9,random_state=0)
test_dataset = df4.drop(train_dataset.index)

train_dataset1 = train_dataset[['bowler','batsman','balls','runsConceded','ER']]
test_dataset1 = test_dataset[['bowler','batsman','balls','runsConceded','ER']]
train_stats = train_dataset1.describe()
train_stats = train_stats.transpose()
#print(train_stats)

train_labels = train_dataset.pop('wicketTaken')
test_labels = test_dataset.pop('wicketTaken')

# Create a Deep Learning model with keras
model = tf.keras.Sequential([
    tf.keras.layers.Embedding(vector_size,16,input_length=5),
    tf.keras.layers.Flatten(),
    keras.layers.Dropout(.2),
    keras.layers.Dense(16),
 
    keras.layers.Dense(8,activation=tf.nn.relu),
    
    keras.layers.Dense(4,activation=tf.nn.relu),
    keras.layers.Dense(1)
  ])

# Print the model summary
#model.summary()
# Use the Adam optimizer with a learning rate of 0.01
#optimizer=keras.optimizers.Adam(learning_rate=.0009, beta_1=0.5, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=True)
#optimizer=keras.optimizers.RMSprop(learning_rate=0.01, rho=0.2, momentum=0.2, epsilon=1e-07)
#optimizer=keras.optimizers.SGD(learning_rate=.009,momentum=0.1) - Works without dropout
optimizer=keras.optimizers.SGD(learning_rate=.01,momentum=0.1)

model.compile(loss='mean_squared_error',
                optimizer=optimizer,
                )

 # Setup the training parameters
#model.compile(loss='binary_crossentropy',optimizer='rmsprop',metrics=['accuracy'])
# Create a model
history=model.fit(
  train_dataset1, train_labels,batch_size=32,
  epochs=40, validation_data = (test_dataset1,test_labels), verbose=1)

e) Plot losses

f) Predict wickets that will be taken by bowlers against random batsmen


df5= df4[['bowler','batsman','balls','runsConceded','ER']]
test1 = df5.sample(n=10)
test1.shape
for i in range(test1.shape[0]):
      print('Bowler :', index2bowlers.get(test1.iloc[i,0]), ", Batsman : ",index2batsmen.get(test1.iloc[i,1]), '- Times wicket Prediction:',model.predict(test1.iloc[[i]]))
1/1 [==============================] - 0s 90ms/step
Bowler : Harbhajan Singh , Batsman :  AM Nayar - Times wicket Prediction: [[1.0114906]]
1/1 [==============================] - 0s 18ms/step
Bowler : T Natarajan , Batsman :  Arshdeep Singh - Times wicket Prediction: [[0.98656166]]
1/1 [==============================] - 0s 19ms/step
Bowler : KK Ahmed , Batsman :  A Mishra - Times wicket Prediction: [[1.0504484]]
1/1 [==============================] - 0s 24ms/step
Bowler : M Muralitharan , Batsman :  F du Plessis - Times wicket Prediction: [[1.0941994]]
1/1 [==============================] - 0s 25ms/step
Bowler : SK Warne , Batsman :  DR Smith - Times wicket Prediction: [[1.0679393]]
1/1 [==============================] - 0s 28ms/step
Bowler : Mohammad Nabi , Batsman :  Ishan Kishan - Times wicket Prediction: [[1.403399]]
1/1 [==============================] - 0s 32ms/step
Bowler : R Bhatia , Batsman :  DJ Thornely - Times wicket Prediction: [[0.89399755]]
1/1 [==============================] - 0s 26ms/step
Bowler : SP Narine , Batsman :  MC Henriques - Times wicket Prediction: [[1.1997008]]
1/1 [==============================] - 0s 19ms/step
Bowler : AS Rajpoot , Batsman :  K Gowtham - Times wicket Prediction: [[0.9911405]]
1/1 [==============================] - 0s 21ms/step
Bowler : K Rabada , Batsman :  P Simran Singh - Times wicket Prediction: [[1.0064855]]

g) The embedding can be visualised using Google’s Embedding Projector, which identifies other batsmen who have similar characteristics. Here Cosine Similarity is used for grouping similar batsmen of IPL

The closest neighbor for AB De Villiers in IPL is SK Raina, then Rohit Sharma as seen in the visualisation below

B. Bowler Recommender T20 (BowlerRecommenderT20M1A.ipynb)

Similar to how batsman was set up,

The steps are

a) Upload data for T20 Batsman vs Bowler with Total runs scored. This will be a sparse matrix

b) Create integer dictionaries for batsman & bowler

c) Add additional features like fours, sixes and strike rate

d) Minimise loss for wicket taken

e) Display embeddings of bowlers using Tensorboard Embeddings Projector

Minimizing the loss for wicket taken using SGD

tf.random.set_seed(4)
vector_size=len(batsman2index)

#Normalize target variable
df4=df31[['bowler','batsman','totalRuns','fours','sixes','ballsFaced']]
df4['normalizedRuns'] = (df4['totalRuns'] -df4['totalRuns'].mean())/df4['totalRuns'].std()
print(df4)
train_dataset = df4.sample(frac=0.8,random_state=0)
test_dataset = df4.drop(train_dataset.index)
train_dataset1 = train_dataset[['batsman','bowler','fours','sixes','ballsFaced']]
test_dataset1 = test_dataset[['batsman','bowler','fours','sixes','ballsFaced']]

train_labels = train_dataset.pop('normalizedRuns')
test_labels = test_dataset.pop('normalizedRuns')
train_labels
print(train_dataset1)

# Create a Deep Learning model with keras
model = tf.keras.Sequential([
    tf.keras.layers.Embedding(vector_size,16,input_length=5),
    tf.keras.layers.Flatten(),
    keras.layers.Dropout(.2),
    keras.layers.Dense(16),
 
    keras.layers.Dense(8,activation=tf.nn.relu),
    
    keras.layers.Dense(4,activation=tf.nn.relu),
    keras.layers.Dense(1)
  ])

# Print the model summary
#model.summary()
# Use the Adam optimizer with a learning rate of 0.01
#optimizer=keras.optimizers.Adam(learning_rate=.0009, beta_1=0.5, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=True)
#optimizer=keras.optimizers.RMSprop(learning_rate=0.001, rho=0.2, momentum=0.2, epsilon=1e-07)
#optimizer=keras.optimizers.SGD(learning_rate=.009,momentum=0.1) - Works without dropout
optimizer=keras.optimizers.SGD(learning_rate=.01,momentum=0.1)

model.compile(loss='mean_squared_error',
                optimizer=optimizer,
                )

 # Setup the training parameters
#model.compile(loss='binary_crossentropy',optimizer='rmsprop',metrics=['accuracy'])
# Create a model
history=model.fit(
  train_dataset1, train_labels,batch_size=32,
  epochs=40, validation_data = (test_dataset1,test_labels), verbose=1)

model.predict(train_dataset1[1:10])
df5= df4[['batsman','bowler','fours','sixes','ballsFaced']]
test1 = df5.sample(n=10)
model.predict(test1)
#(model.predict(test1)* df4['totalRuns'].std()) + df4['totalRuns'].mean()
for i in range(test1.shape[0]):
        print('Batsman :', index2batsman.get(test1.iloc[i,0]), ", Bowler : ",index2bowler.get(test1.iloc[i,1]), '- Total runs Prediction:',(model.predict(test1.iloc[i])* df4['totalRuns'].std()) + df4['totalRuns'].mean())
1/1 [==============================] - 0s 396ms/step
1/1 [==============================] - 0s 112ms/step
1/1 [==============================] - 0s 183ms/step
Batsman : G Chohan , Bowler :  Khawar Ali - Total runs Prediction: [[1.8883028]]
1/1 [==============================] - 0s 56ms/step
Batsman : Umar Akmal , Bowler :  LJ Wright - Total runs Prediction: [[9.305391]]
1/1 [==============================] - 0s 68ms/step
Batsman : M Shumba , Bowler :  Simi Singh - Total runs Prediction: [[19.662743]]
1/1 [==============================] - 0s 30ms/step
Batsman : CH Gayle , Bowler :  RJW Topley - Total runs Prediction: [[16.854687]]
1/1 [==============================] - 0s 39ms/step
Batsman : BA King , Bowler :  Taskin Ahmed - Total runs Prediction: [[3.5154686]]
1/1 [==============================] - 0s 102ms/step
Batsman : KD Shah , Bowler :  Avesh Khan - Total runs Prediction: [[8.411661]]
1/1 [==============================] - 0s 38ms/step
Batsman : ST Jayasuriya , Bowler :  SCJ Broad - Total runs Prediction: [[5.867449]]
1/1 [==============================] - 0s 45ms/step
Batsman : AB de Villiers , Bowler :  Saeed Ajmal - Total runs Prediction: [[15.150892]]
1/1 [==============================] - 0s 46ms/step
Batsman : SV Samson , Bowler :  J Little - Total runs Prediction: [[10.44426]]
1/1 [==============================] - 0s 102ms/step
Batsman : Zawar Farid , Bowler :  GJ Delany - Total runs Prediction: [[1.9770675]]

Identifying similar bowlers using Embeddings Projector for T20

Bhuvaneshwar Kumar’s performance is closest to CR Woakes

Note: Incidentally the accuracy in the above model was not too good. I may work on this again later!

C) Bowler Embeddings IPL – Grouping similar bowlers of IPL with Embeddings Projector (BowlerRecommenderIPLA.ipynb)

D) Batting Embeddings T20 – Grouping similar batsmen of T20 (BatsmanRecommenderT20MA.ipynb)

The Tensorboard Pmbeddings projector is also interesting. There are multiple ways the data can be visualised namely UMAP, T-SNE, PCA(included). You could play with it.

As mentioned above the Colab notebooks and data are available at Github embeddings

The ability to identify batsmen & bowlers who would perform similarly against specific bowling attacks coupled with the average runs & strike rate should give a good measure of a player’s performance.

Take a look at some of my other posts

To see all posts click Index of posts

Deconstructing Convolutional Neural Networks with Tensorflow and Keras

I have been very fascinated by how Convolution Neural Networks have been able to, so efficiently, do image classification and image recognition CNN’s have been very successful in in both these tasks. A good paper that explores the workings of a CNN Visualizing and Understanding Convolutional Networks by Matthew D Zeiler and Rob Fergus. They show how through a reverse process of convolution using a deconvnet.

In their paper they show how by passing the feature map through a deconvnet ,which does the reverse process of the convnet, they can reconstruct what input pattern originally caused a given activation in the feature map

In the paper they say “A deconvnet can be thought of as a convnet model that uses the same components (filtering, pooling) but in reverse, so instead of mapping pixels to features, it does the opposite. An input image is presented to the CNN and features activation computed throughout the layers. To examine a given convnet activation, we set all other activations in the layer to zero and pass the feature maps as input to the attached deconvnet layer. Then we successively (i) unpool, (ii) rectify and (iii) filter to reconstruct the activity in the layer beneath that gave rise to the chosen activation. This is then repeated until input pixel space is reached.”

I started to scout the internet to see how I can implement this reverse process of Convolution to understand what really happens under the hood of a CNN. There are a lot of good articles and blogs, but I found this post Applied Deep Learning – Part 4: Convolutional Neural Networks take the visualization of the CNN one step further.

This post takes VGG16 as the pre-trained network and then uses this network to display the intermediate visualizations. While this post was very informative and also the visualizations of the various images were very clear, I wanted to simplify the problem for my own understanding.

Hence I decided to take the MNIST digit classification as my base problem. I created a simple 3 layer CNN which gives close to 99.1% accuracy and decided to see if I could do the visualization.

As mentioned in the above post, there are 3 major visualisations

Feature activations at the layer
Visualisation of the filters
Visualisation of the class outputs

Feature Activation – This visualization the feature activation at the 3 different layers for a given input image. It can be seen that first layer activates based on the edge of the image. Deeper layers activate in a more abstract way.

Visualization of the filters: This visualization shows what patterns the filters respond maximally to. This is implemented in Keras here

To do this the following is repeated in a loop

Choose a loss function that maximizes the value of a convnet filter activation
Do gradient ascent (maximization) in input space that increases the filter activation

Visualizing Class Outputs of the MNIST Convnet: This process is similar to determining the filter activation. Here the convnet is made to generate an image that represents the category maximally.

You can access the Google colab notebook here – Deconstructing Convolutional Neural Networks in Tensoflow and Keras

import numpy as np
import pandas as pd
import os
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D, Input
from keras.models import Model
from sklearn.model_selection import train_test_split
from keras.utils import np_utils

Using TensorFlow backend.

In [0]:

mnist=tf.keras.datasets.mnist
# Set training and test data and labels
(training_images,training_labels),(test_images,test_labels)=mnist.load_data()

In [0]:

#Normalize training data
X =np.array(training_images).reshape(training_images.shape[0],28,28,1) 
# Normalize the images by dividing by 255.0
X = X/255.0
X.shape
# Use one hot encoding for the labels
Y = np_utils.to_categorical(training_labels, 10)
Y.shape
# Split training data into training and validation data in the ratio of 80:20
X_train, X_validation, y_train, y_validation = train_test_split(X,Y,test_size=0.20, random_state=42)

In [4]:

# Normalize test data
X_test =np.array(test_images).reshape(test_images.shape[0],28,28,1) 
X_test=X_test/255.0
#Use OHE for the test labels
Y_test = np_utils.to_categorical(test_labels, 10)
X_test.shape

Out[4]:

(10000, 28, 28, 1)

Display data

Display the training data and the corresponding labels

In [5]:

print(training_labels[0:10])
f, axes = plt.subplots(1, 10, sharey=True,figsize=(10,10))
for i,ax in enumerate(axes.flat):
    ax.axis('off')
    ax.imshow(X[i,:,:,0],cmap="gray")

Create a Convolutional Neural Network

The CNN consists of 3 layers

Conv2D of size 28 x 28 with 24 filters
Perform Max pooling
Conv2D of size 14 x 14 with 48 filters
Perform max pooling
Conv2d of size 7 x 7 with 64 filters
Flatten
Use Dense layer with 128 units
Perform 25% dropout
Perform categorical cross entropy with softmax activation function

In [0]:

num_classes=10
inputs = Input(shape=(28,28,1))
x = Conv2D(24,kernel_size=(3,3),padding='same',activation="relu")(inputs)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(48, (3, 3), padding='same',activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(64, (3, 3), padding='same',activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Flatten()(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.25)(x)
output = Dense(num_classes,activation="softmax")(x)

model = Model(inputs,output)

model.compile(loss='categorical_crossentropy', 
          optimizer='adam', 
          metrics=['accuracy'])

Summary of CNN

Display the summary of CNN

In [7]:

model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 28, 28, 24)        240       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 24)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 14, 14, 48)        10416     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 48)          0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 7, 7, 64)          27712     
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 3, 3, 64)          0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 576)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 128)               73856     
_________________________________________________________________
dropout_1 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 10)                1290      
=================================================================
Total params: 113,514
Trainable params: 113,514
Non-trainable params: 0
_________________________________________________________________

Perform Gradient descent and validate with the validation data

In [8]:

epochs = 20
batch_size=256
history = model.fit(X_train,y_train,
         epochs=epochs,
         batch_size=batch_size,
         validation_data=(X_validation,y_validation))

————————————————

acc = history.history[ ‘accuracy’ ]

val_acc = history.history[ ‘val_accuracy’ ]

loss = history.history[ ‘loss’ ]

val_loss = history.history[‘val_loss’ ]

epochs = range(len(acc)) # Get number of epochs

#————————————————

# Plot training and validation accuracy per epoch

#————————————————

plt.plot ( epochs, acc,label=”training accuracy” )

plt.plot ( epochs, val_acc, label=’validation acuracy’ )

plt.title (‘Training and validation accuracy’)

plt.legend()

plt.figure()

#————————————————

# Plot training and validation loss per epoch

#————————————————

plt.plot ( epochs, loss , label=”training loss”)

plt.plot ( epochs, val_loss,label=”validation loss” )

plt.title (‘Training and validation loss’ )

plt.legend()

Test model on test data

f, axes = plt.subplots(1, 10, sharey=True,figsize=(10,10))

for i,ax in enumerate(axes.flat):

ax.axis(‘off’)

ax.imshow(X_test[i,:,:,0],cmap=”gray”)

l=[]
for i in range(10):
  x=X_test[i].reshape(1,28,28,1)
  y=model.predict(x)
  m = np.argmax(y, axis=1)
  print(m)

[7]
[2]
[1]
[0]
[4]
[1]
[4]
[9]
[5]
[9]

Generate the filter activations at the intermediate CNN layers

In [12]:

img = test_images[51].reshape(1,28,28,1)
fig = plt.figure(figsize=(5,5))
print(img.shape)
plt.imshow(img[0,:,:,0],cmap="gray")
plt.axis('off')

Display the activations at the intermediate layers

This displays the intermediate activations as the image passes through the filters and generates these feature maps

In [13]:

layer_names = ['conv2d_4', 'conv2d_5', 'conv2d_6']

layer_outputs = [layer.output for layer in model.layers if 'conv2d' in layer.name]
activation_model = Model(inputs=model.input,outputs=layer_outputs)
intermediate_activations = activation_model.predict(img)
images_per_row = 8
max_images = 8

for layer_name, layer_activation in zip(layer_names, intermediate_activations):
    print(layer_name,layer_activation.shape)
    n_features = layer_activation.shape[-1]
    print("features=",n_features)
    n_features = min(n_features, max_images)
    print(n_features)

    size = layer_activation.shape[1]
    print("size=",size)
    n_cols = n_features // images_per_row
    display_grid = np.zeros((size * n_cols, images_per_row * size))


    for col in range(n_cols):
      for row in range(images_per_row):
          channel_image = layer_activation[0,:, :, col * images_per_row + row]

          channel_image -= channel_image.mean()
          channel_image /= channel_image.std()
          channel_image *= 64
          channel_image += 128
          channel_image = np.clip(channel_image, 0, 255).astype('uint8')
          display_grid[col * size : (col + 1) * size,
                         row * size : (row + 1) * size] = channel_image
    scale = 2. / size
    plt.figure(figsize=(scale * display_grid.shape[1],
                        scale * display_grid.shape[0]))
    plt.axis('off')
    plt.title(layer_name)
    plt.grid(False)
    plt.imshow(display_grid, aspect='auto', cmap='viridis')
    
plt.show()

It can be seen that at the higher layers only abstract features of the input image are captured

# To fix the ImportError: cannot import name 'imresize' in the next cell. Run this cell. Then comment and restart and run all
#!pip install scipy==1.1.0

Visualize the pattern that the filters respond to maximally

Choose a loss function that maximizes the value of the CNN filter in a given layer
Start from a blank input image.
Do gradient ascent in input space. Modify input values so that the filter activates more
Repeat this in a loop.

In [14]:

from vis.visualization import visualize_activation, get_num_filters
from vis.utils import utils
from vis.input_modifiers import Jitter

max_filters = 24
selected_indices = []
vis_images = [[], [], [], [], []]
i = 0
selected_filters = [[0, 3, 11, 15, 16, 17, 18, 22], 
    [8, 21, 23, 25, 31, 32, 35, 41], 
    [2, 7, 11, 14, 19, 26, 35, 48]]

# Set the layers
layer_name = ['conv2d_4', 'conv2d_5', 'conv2d_6']
# Set the layer indices
layer_idx = [1,3,5]
for layer_name,layer_idx in zip(layer_name,layer_idx):


    # Visualize all filters in this layer.
    if selected_filters:
        filters = selected_filters[i]
    else:
        # Randomly select filters
        filters = sorted(np.random.permutation(get_num_filters(model.layers[layer_idx]))[:max_filters])
    selected_indices.append(filters)

    # Generate input image for each filter.
    # Loop through the selected filters in each layer and generate the activation of these filters
    for idx in filters:
        img = visualize_activation(model, layer_idx, filter_indices=idx, tv_weight=0., 
                                   input_modifiers=[Jitter(0.05)], max_iter=300) 
        vis_images[i].append(img)

    # Generate stitched image palette with 4 cols so we get 2 rows.
    stitched = utils.stitch_images(vis_images[i], cols=4)    
    plt.figure(figsize=(20, 30))
    plt.title(layer_name)
    plt.axis('off')
    stitched = stitched.reshape(1,61,127,1)
    plt.imshow(stitched[0,:,:,0])
    plt.show()
    i += 1

from vis.utils import utils
new_vis_images = [[], [], [], [], []]
i = 0
layer_name = ['conv2d_4', 'conv2d_5', 'conv2d_6']
layer_idx = [1,3,5]
for layer_name,layer_idx in zip(layer_name,layer_idx):
   
    # Generate input image for each filter.
    for j, idx in enumerate(selected_indices[i]):
        img = visualize_activation(model, layer_idx, filter_indices=idx, 
                                   seed_input=vis_images[i][j], input_modifiers=[Jitter(0.05)], max_iter=300) 
        #img = utils.draw_text(img, 'Filter {}'.format(idx))  
        new_vis_images[i].append(img)

    stitched = utils.stitch_images(new_vis_images[i], cols=4)   
    plt.figure(figsize=(20, 30))
    plt.title(layer_name)
    plt.axis('off')
    print(stitched.shape)
    stitched = stitched.reshape(1,61,127,1)
    plt.imshow(stitched[0,:,:,0])
    plt.show()
    i += 1

Visualizing Class Outputs

Here the CNN will generate the image that maximally represents the category. Each of the output represents one of the digits as can be seen below

In [16]:

from vis.utils import utils
from keras import activations
codes = '''
zero 0
one 1
two 2
three 3
four 4
five 5
six 6
seven 7
eight 8
nine 9
'''
layer_idx=10
initial = []
images = []
tuples = []
# Swap softmax with linear for better visualization
model.layers[layer_idx].activation = activations.linear
model = utils.apply_modifications(model)
for line in codes.split('\n'):
    if not line:
        continue
    name, idx = line.rsplit(' ', 1)
    idx = int(idx)
    img = visualize_activation(model, layer_idx, filter_indices=idx, 
                               tv_weight=0., max_iter=300, input_modifiers=[Jitter(0.05)])

    initial.append(img)
    tuples.append((name, idx))

i = 0
for name, idx in tuples:
    img = visualize_activation(model, layer_idx, filter_indices=idx,
                               seed_input = initial[i], max_iter=300, input_modifiers=[Jitter(0.05)])
    #img = utils.draw_text(img, name) # Unable to display text on gray scale image
    i += 1
    images.append(img)

stitched = utils.stitch_images(images, cols=4)
plt.figure(figsize=(20, 20))
plt.axis('off')
stitched = stitched.reshape(1,94,127,1)
plt.imshow(stitched[0,:,:,0])

plt.show()

In the grid below the class outputs show the MNIST digits to which output responds to maximally. We can see the ghostly outline
of digits 0 – 9. We can clearly see the outline if 0,1, 2,3,4,5 (yes, it is there!),6,7, 8 and 9. If you look at this from a little distance the digits are clearly visible. Isn’t that really cool!!

Conclusion:

It is really interesting to see the class outputs which show the image to which the class output responds to maximally. In the
post Applied Deep Learning – Part 4: Convolutional Neural Networks the class output show much more complicated images and is worth a look. It is really interesting to note that the model has adjusted the filter values and the weights of the fully connected network to maximally respond to the MNIST digits

References

1. Visualizing and Understanding Convolutional Networks
2. Applied Deep Learning – Part 4: Convolutional Neural Networks
3. Visualizing Intermediate Activations of a CNN trained on the MNIST Dataset
4. How convolutional neural networks see the world
5. Keras – Activation_maximization

Also see

1. Using Reinforcement Learning to solve Gridworld
2. Deep Learning from first principles in Python, R and Octave – Part 8
3. Cricketr learns new tricks : Performs fine-grained analysis of players
4. Video presentation on Machine Learning, Data Science, NLP and Big Data – Part 1
5. Big Data-2: Move into the big league:Graduate from R to SparkR
6. OpenCV: Fun with filters and convolution
7. Powershell GUI – Adding bells and whistles

To see all posts click Index of posts

The mechanics of Convolutional Neural Networks in Tensorflow and Keras

Convolutional Neural Networks (CNNs), have been very popular in the last decade or so. CNNs have been used in multiple applications like image recognition, image classification, facial recognition, neural style transfer etc. CNN’s have been extremely successful in handling these kind of problems. How do they work? What makes them so successful? What is the principle behind CNN’s ?

Note: this post is based on two Coursera courses I did, namely namely Deep Learning specialisation by Prof Andrew Ng and Tensorflow Specialisation by Laurence Moroney.

In this post I show you how CNN’s work. To understand how CNNs work, we need to understand the concept behind machine learning algorithms. If you take a simple machine learning algorithm in which you are trying to do multi-class classification using softmax or binary classification with the sigmoid function, for a set of for a set of input features against a target variable we need to create an objective function of the input features versus the target variable. Then we need to minimise this objective function, while performing gradient descent, such that the cost is the lowest. This will give the set of weights for the different variables in the objective function.

The central problem in ML algorithms is to do feature selection, i.e. we need to find the set of features that actually influence the target. There are various methods for doing features selection – best fit, forward fit, backward fit, ridge and lasso regression. All these methods try to pick out the predictors that influence the output most, by making the weights of the other features close to zero. Please look at my post – Practical Machine Learning in R and Python – Part 3, where I show you the different methods for doing features selection.

In image classification or Image recognition we need to find the important features in the image. How do we do that? Many years back, have played around with OpenCV. While working with OpenCV I came across are numerous filters like the Sobel ,the Laplacian, Canny, Gaussian filter et cetera which can be used to identify key features of the image. For example the Canny filter feature can be used for edge detection, Gaussian for smoothing, Sobel for determining the derivative and we have other filters for detecting vertical or horizontal edges. Take a look at my post Computer Vision: Ramblings on derivatives, histograms and contours So for handling images we need to apply these filters to pick out the key features of the image namely the edges and other features. So rather than using the entire image’s pixels against the target class we can pick out the features from the image and use that as predictors of the target output.

Note: that in Convolutional Neural Network, fixed filter values like the those shown above are not used directly. Rather the filter values are learned through back propagation and gradient descent as shown below.

In CNNs the filter values are considered to be weights which are then learned and updated in each forward/backward propagation cycle much like the way a fully connected Deep Learning Network learns the weights of the network.

Here is a short derivation of the most important parts of how a CNNs work

The convolution of a filter F with the input X can be represented as.

Convolving we get

This the forward propagation as it passes through a non-linear function like Relu

To go through back propagation we need to compute the $\partial L$ at every node of Convolutional Neural network

The loss with respect to the output is $\partial L/\partial O$ . $\partial O/\partial X$ & $\partial O/\partial F$ are the local derivatives

We need these local derivatives because we can learn the filter values using gradient descent

where $\alpha$ is the learning rate. Also $\partial L/\partial X$ is the loss which is back propagated to the previous layers. You can see the detailed derivation of back propagation in my post Deep Learning from first principles in Python, R and Octave – Part 3 in a L-layer, multi-unit Deep Learning network.

In the fully connected layers the weights associated with each connection is computed in every cycle of forward and backward propagation using gradient descent. Similarly, the filter values are also computed and updated in each forward and backward propagation cycle. This is done so as to minimize the loss at the output layer.

By using the chain rule and simplifying the back propagation for the Convolutional layers we get these 2 equations. The first equation is used to learn the filter values and the second is used pass the loss to layers before

(for the detailed derivation see Convolutions and Backpropagations

An important aspect of performing convolutions is to reduce the size of the flattened image that is passed into the fully connected DL network. Successively convolving with 2D filters and doing a max pooling helps to reduce the size of the features that we can use for learning the images. Convolutions also enable a sparsity of connections as you can see in the diagram below. In the LeNet-5 Convolution Neural Network of Yann Le Cunn, successive convolutions reduce the image size from 28 x 28=784 to 120 flattened values.

Here is an interesting Deep Learning problem. Convolutions help in picking out important features of images and help in image classification/ detection. What would be its equivalent if we wanted to identify the Carnatic ragam of a song? A Carnatic ragam is roughly similar to Western scales (major, natural, melodic, blues) with all its modes Lydian, Aeolion, Phyrgian etc. Except in the case of the ragams, it is more nuanced, complex and involved. Personally, I can rarely identify a ragam on which a carnatic song is based (I am tone deaf when it comes to identifying ragams). I have come to understand that each Carnatic ragam has its own character, which is made up of several melodic phrases which are unique to that flavor of a ragam. What operation like convolution would be needed so that we can pick out these unique phrases in a Carnatic ragam? Of course, we would need to use it in Recurrent Neural Networks with LSTMs as a song is a time sequence of notes to identify sequences. Nevertheless, if there was some operation with which we can pick up the distinct, unique phrases from a song and then run it through a classifier, maybe we would be able to identify the ragam of the song.

Below I implement 3 simple CNN using the Dogs vs Cats Dataset from Kaggle. The first CNN uses regular Convolutions a Fully connected network to classify the images. The second approach uses Image Augmentation. For some reason, I did not get a better performance with Image Augumentation. Thirdly I use the pre-trained Inception v3 network.

1. Basic Convolutional Neural Network in Tensorflow & Keras

You can view the Colab notebook here – Cats_vs_dogs_1.ipynb

Here some important parts of the notebook

Create CNN Model

Use 3 Convolution + Max pooling layers with 32,64 and 128 filters respectively
Flatten the data
Have 2 Fully connected layers with 128, 512 neurons with relu activation
Use sigmoid for binary classification

In [0]:

model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(32,(3,3),activation='relu',input_shape=(150,150,3)),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128,activation='relu'),
    tf.keras.layers.Dense(512,activation='relu'),
    tf.keras.layers.Dense(1,activation='sigmoid')
])

Print model summary

In [13]:

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
flatten (Flatten)            (None, 36992)             0         
_________________________________________________________________
dense (Dense)                (None, 128)               4735104   
_________________________________________________________________
dense_1 (Dense)              (None, 512)               66048     
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 513       
=================================================================
Total params: 4,894,913
Trainable params: 4,894,913
Non-trainable params: 0
_________________________________________________________________

Use the Adam Optimizer with binary cross entropy

model.compile(optimizer='adam',
             loss='binary_crossentropy',
             metrics=['accuracy'])

Perform Gradient Descent

Do Gradient Descent for 15 epochs

history=model.fit(train_generator,
                 validation_data=validation_generator,
                 steps_per_epoch=100,
                 epochs=15,
                 validation_steps=50,
                 verbose=2)

Epoch 1/15
100/100 - 13s - loss: 0.6821 - accuracy: 0.5425 - val_loss: 0.6484 - val_accuracy: 0.6131
Epoch 2/15
100/100 - 13s - loss: 0.6227 - accuracy: 0.6456 - val_loss: 0.6161 - val_accuracy: 0.6394
Epoch 3/15
100/100 - 13s - loss: 0.5975 - accuracy: 0.6719 - val_loss: 0.5558 - val_accuracy: 0.7206
Epoch 4/15
100/100 - 13s - loss: 0.5480 - accuracy: 0.7241 - val_loss: 0.5431 - val_accuracy: 0.7138
Epoch 5/15
100/100 - 13s - loss: 0.5182 - accuracy: 0.7447 - val_loss: 0.4839 - val_accuracy: 0.7606
Epoch 6/15
100/100 - 13s - loss: 0.4773 - accuracy: 0.7781 - val_loss: 0.5029 - val_accuracy: 0.7506
Epoch 7/15
100/100 - 13s - loss: 0.4466 - accuracy: 0.7972 - val_loss: 0.4573 - val_accuracy: 0.7912
Epoch 8/15
100/100 - 13s - loss: 0.4395 - accuracy: 0.7997 - val_loss: 0.4252 - val_accuracy: 0.8119
Epoch 9/15
100/100 - 13s - loss: 0.4314 - accuracy: 0.8019 - val_loss: 0.4931 - val_accuracy: 0.7481
Epoch 10/15
100/100 - 13s - loss: 0.4309 - accuracy: 0.7969 - val_loss: 0.4203 - val_accuracy: 0.8109
Epoch 11/15
100/100 - 13s - loss: 0.4329 - accuracy: 0.7916 - val_loss: 0.4189 - val_accuracy: 0.8069
Epoch 12/15
100/100 - 13s - loss: 0.4248 - accuracy: 0.8050 - val_loss: 0.4476 - val_accuracy: 0.7925
Epoch 13/15
100/100 - 13s - loss: 0.3868 - accuracy: 0.8306 - val_loss: 0.3900 - val_accuracy: 0.8236
Epoch 14/15
100/100 - 13s - loss: 0.3710 - accuracy: 0.8328 - val_loss: 0.4520 - val_accuracy: 0.7900
Epoch 15/15
100/100 - 13s - loss: 0.3654 - accuracy: 0.8353 - val_loss: 0.3999 - val_accuracy: 0.8100

Plot results

- Plot training and validation accuracy

Plot training and validation loss

#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc      = history.history[     'accuracy' ]
val_acc  = history.history[ 'val_accuracy' ]
loss     = history.history[    'loss' ]
val_loss = history.history['val_loss' ]

epochs   = range(len(acc)) # Get number of epochs

#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot  ( epochs,     acc,label="training accuracy" )
plt.plot  ( epochs, val_acc, label='validation acuracy' )
plt.title ('Training and validation accuracy')
plt.legend()

plt.figure()

#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot  ( epochs,     loss , label="training loss")
plt.plot  ( epochs, val_loss,label="validation loss" )
plt.title ('Training and validation loss'   )
plt.legend()

2. CNN with Image Augmentation

You can check the Cats_vs_Dogs_2.ipynb

Including the important parts of this implementation below

Use Image Augumentation

Use Image Augumentation to improve performance

Use the same model parameters as before
Perform the following image augmentation
- width, height shift
- shear and zoom
Note: Adding rotation made the performance worse

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
model = tf.keras.models.Sequential([
    tf.keras.layers.Conv2D(32,(3,3),activation='relu',input_shape=(150,150,3)),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
    tf.keras.layers.MaxPooling2D(2,2),
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128,activation='relu'),
    tf.keras.layers.Dense(512,activation='relu'),
    tf.keras.layers.Dense(1,activation='sigmoid')
])


train_datagen = ImageDataGenerator(
      rescale=1./255,
      #rotation_range=90,
      width_shift_range=0.2,
      height_shift_range=0.2,
      shear_range=0.2,
      zoom_range=0.2)
      #horizontal_flip=True,
      #fill_mode='nearest')

validation_datagen = ImageDataGenerator(rescale=1./255)
#
train_generator = train_datagen.flow_from_directory(train_dir,
                                                    batch_size=32,
                                                    class_mode='binary',
                                                    target_size=(150, 150))     
# --------------------
# Flow validation images in batches of 20 using test_datagen generator
# --------------------
validation_generator =  validation_datagen.flow_from_directory(validation_dir,
                                                         batch_size=32,
                                                         class_mode  = 'binary',
                                                         target_size = (150, 150))

# Use Adam Optmizer 
model.compile(optimizer='adam',
             loss='binary_crossentropy',
             metrics=['accuracy'])

Found 20000 images belonging to 2 classes.
Found 5000 images belonging to 2 classes.

Perform Gradient Descent

history=model.fit(train_generator,
                 validation_data=validation_generator,
                 steps_per_epoch=100,
                 epochs=15,
                 validation_steps=50,
                 verbose=2)

Epoch 1/15
100/100 - 27s - loss: 0.5716 - accuracy: 0.6922 - val_loss: 0.4843 - val_accuracy: 0.7744
Epoch 2/15
100/100 - 27s - loss: 0.5575 - accuracy: 0.7084 - val_loss: 0.4683 - val_accuracy: 0.7750
Epoch 3/15
100/100 - 26s - loss: 0.5452 - accuracy: 0.7228 - val_loss: 0.4856 - val_accuracy: 0.7665
Epoch 4/15
100/100 - 27s - loss: 0.5294 - accuracy: 0.7347 - val_loss: 0.4654 - val_accuracy: 0.7812
Epoch 5/15
100/100 - 27s - loss: 0.5352 - accuracy: 0.7350 - val_loss: 0.4557 - val_accuracy: 0.7981
Epoch 6/15
100/100 - 26s - loss: 0.5136 - accuracy: 0.7453 - val_loss: 0.4964 - val_accuracy: 0.7621
Epoch 7/15
100/100 - 27s - loss: 0.5249 - accuracy: 0.7334 - val_loss: 0.4959 - val_accuracy: 0.7556
Epoch 8/15
100/100 - 26s - loss: 0.5035 - accuracy: 0.7497 - val_loss: 0.4555 - val_accuracy: 0.7969
Epoch 9/15
100/100 - 26s - loss: 0.5024 - accuracy: 0.7487 - val_loss: 0.4675 - val_accuracy: 0.7728
Epoch 10/15
100/100 - 27s - loss: 0.5015 - accuracy: 0.7500 - val_loss: 0.4276 - val_accuracy: 0.8075
Epoch 11/15
100/100 - 26s - loss: 0.5002 - accuracy: 0.7581 - val_loss: 0.4193 - val_accuracy: 0.8131
Epoch 12/15
100/100 - 27s - loss: 0.4733 - accuracy: 0.7706 - val_loss: 0.5209 - val_accuracy: 0.7398
Epoch 13/15
100/100 - 27s - loss: 0.4999 - accuracy: 0.7538 - val_loss: 0.4109 - val_accuracy: 0.8075
Epoch 14/15
100/100 - 27s - loss: 0.4550 - accuracy: 0.7859 - val_loss: 0.3770 - val_accuracy: 0.8288
Epoch 15/15
100/100 - 26s - loss: 0.4688 - accuracy: 0.7688 - val_loss: 0.4764 - val_accuracy: 0.7786

Plot results

Plot training and validation accuracy
Plot training and validation loss

In [15]:

import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc      = history.history[     'accuracy' ]
val_acc  = history.history[ 'val_accuracy' ]
loss     = history.history[    'loss' ]
val_loss = history.history['val_loss' ]

epochs   = range(len(acc)) # Get number of epochs

#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot  ( epochs,     acc,label="training accuracy" )
plt.plot  ( epochs, val_acc, label='validation acuracy' )
plt.title ('Training and validation accuracy')
plt.legend()

plt.figure()

#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot  ( epochs,     loss , label="training loss")
plt.plot  ( epochs, val_loss,label="validation loss" )
plt.title ('Training and validation loss'   )
plt.legend()

Implementation using Inception Network V3

The implementation is in the Colab notebook Cats_vs_Dog_3.ipynb

This is implemented as below

Use Inception V3

import os

from tensorflow.keras import layers
from tensorflow.keras import Model

  
from tensorflow.keras.applications.inception_v3 import InceptionV3
pre_trained_model = InceptionV3(input_shape = (150, 150, 3), 
                                include_top = False, 
                                weights = 'imagenet')


for layer in pre_trained_model.layers:
  layer.trainable = False
  
# pre_trained_model.summary()

last_layer = pre_trained_model.get_layer('mixed7')
print('last layer output shape: ', last_layer.output_shape)
last_output = last_layer.output

Downloading data from https://storage.googleapis.com/tensorflow/keras-applications/inception_v3/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5
87916544/87910968 [==============================] - 1s 0us/step
last layer output shape:  (None, 7, 7, 768)

Use Layer 7 of Inception Network

Use Image Augumentation
Use Adam Optimizer

In [0]:

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# Flatten the output layer to 1 dimension
x = layers.Flatten()(last_output)
# Add a fully connected layer with 1,024 hidden units and ReLU activation
x = layers.Dense(1024, activation='relu')(x)
# Add a dropout rate of 0.2
x = layers.Dropout(0.2)(x)                  
# Add a final sigmoid layer for classification
x = layers.Dense  (1, activation='sigmoid')(x)           

model = Model( pre_trained_model.input, x) 
#train_datagen = ImageDataGenerator( rescale = 1.0/255. )
#validation_datagen = ImageDataGenerator( rescale = 1.0/255. )

train_datagen = ImageDataGenerator(
      rescale=1./255,
      #rotation_range=90,
      width_shift_range=0.2,
      height_shift_range=0.2,
      shear_range=0.2,
      zoom_range=0.2)
      #horizontal_flip=True,
      #fill_mode='nearest')

validation_datagen = ImageDataGenerator(rescale=1./255)
#
train_generator = train_datagen.flow_from_directory(train_dir,
                                                    batch_size=32,
                                                    class_mode='binary',
                                                    target_size=(150, 150))     
# --------------------
# Flow validation images in batches of 20 using test_datagen generator
# --------------------
validation_generator =  validation_datagen.flow_from_directory(validation_dir,
                                                         batch_size=32,
                                                         class_mode  = 'binary',
                                                         target_size = (150, 150))


model.compile(optimizer='adam',
             loss='binary_crossentropy',
             metrics=['accuracy'])

Found 20000 images belonging to 2 classes.
Found 5000 images belonging to 2 classes.

Fit model

history=model.fit(train_generator,
                 validation_data=validation_generator,
                 steps_per_epoch=100,
                 epochs=15,
                 validation_steps=50,
                 verbose=2)

Epoch 1/15
100/100 - 31s - loss: 0.5961 - accuracy: 0.8909 - val_loss: 0.1919 - val_accuracy: 0.9456
Epoch 2/15
100/100 - 30s - loss: 0.2002 - accuracy: 0.9259 - val_loss: 0.1025 - val_accuracy: 0.9550
Epoch 3/15
100/100 - 30s - loss: 0.1618 - accuracy: 0.9366 - val_loss: 0.0920 - val_accuracy: 0.9581
Epoch 4/15
100/100 - 29s - loss: 0.1442 - accuracy: 0.9381 - val_loss: 0.0960 - val_accuracy: 0.9600
Epoch 5/15
100/100 - 30s - loss: 0.1402 - accuracy: 0.9381 - val_loss: 0.0703 - val_accuracy: 0.9794
Epoch 6/15
100/100 - 30s - loss: 0.1437 - accuracy: 0.9413 - val_loss: 0.1090 - val_accuracy: 0.9531
Epoch 7/15
100/100 - 30s - loss: 0.1325 - accuracy: 0.9428 - val_loss: 0.0756 - val_accuracy: 0.9670
Epoch 8/15
100/100 - 29s - loss: 0.1341 - accuracy: 0.9491 - val_loss: 0.0625 - val_accuracy: 0.9737
Epoch 9/15
100/100 - 29s - loss: 0.1186 - accuracy: 0.9513 - val_loss: 0.0934 - val_accuracy: 0.9581
Epoch 10/15
100/100 - 29s - loss: 0.1171 - accuracy: 0.9513 - val_loss: 0.0642 - val_accuracy: 0.9727
Epoch 11/15
100/100 - 29s - loss: 0.1018 - accuracy: 0.9591 - val_loss: 0.0930 - val_accuracy: 0.9606
Epoch 12/15
100/100 - 29s - loss: 0.1190 - accuracy: 0.9541 - val_loss: 0.0737 - val_accuracy: 0.9719
Epoch 13/15
100/100 - 29s - loss: 0.1223 - accuracy: 0.9494 - val_loss: 0.0740 - val_accuracy: 0.9695
Epoch 14/15
100/100 - 29s - loss: 0.1158 - accuracy: 0.9516 - val_loss: 0.0659 - val_accuracy: 0.9744
Epoch 15/15
100/100 - 29s - loss: 0.1168 - accuracy: 0.9591 - val_loss: 0.0788 - val_accuracy: 0.9669

Plot results

Plot training and validation accuracy
Plot training and validation loss

In [14]:

import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc      = history.history[     'accuracy' ]
val_acc  = history.history[ 'val_accuracy' ]
loss     = history.history[    'loss' ]
val_loss = history.history['val_loss' ]

epochs   = range(len(acc)) # Get number of epochs

#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot  ( epochs,     acc,label="training accuracy" )
plt.plot  ( epochs, val_acc, label='validation acuracy' )
plt.title ('Training and validation accuracy')
plt.legend()

plt.figure()

#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot  ( epochs,     loss , label="training loss")
plt.plot  ( epochs, val_loss,label="validation loss" )
plt.title ('Training and validation loss'   )
plt.legend()

I intend to do some interesting stuff with Convolutional Neural Networks.

Watch this space!

To see all posts click Index of posts

Big Data 6: The T20 Dance of Apache NiFi and yorkpy

“I don’t count my sit-ups. I only start counting once it starts hurting. ”

Muhammad Ali

“Hard work beats talent when talent doesn’t work hard.”

Tim Notke

In my previous post Big Data 5: kNiFI-ing through cricket data with Apache NiFi and yorkpy, I created a Big Data Pipeline that takes raw data in YAML format from a Cricsheet to processing and ranking IPL T20 players. In that post I had mentioned that we could create a similar pipeline to create a real time dashboard of IPL Analytics. I could have have done this but I needed to know how to create a Web UI. After digging and poking around, I have been able to create a simple Web UI running off Apache Web server. This UI uses basic JQuery and CSS to display a real time IPL T20 dashboard. As in my previous post, this is an end-2-end Big Data pipeline which can handle large data sets at scheduled times, process them and generate real time dashboards.

We could imagine an inter-galactic T20 championship league where T20 data comes in every hour or sooner and we need to perform analytics to see if us earthlings are any better than people with pointy heads or little green men. The NiFi pipeline could be used as-is, however the yorkpy package would have to be rewritten in Pyspark. That is in another eon, though.

My package yorkpy has around ~45+ functions which fall in the following main categories

1. Pitching yorkpy . short of good length to IPL – Part 1 :Class 1: This includes functions that convert the yaml data of IPL matches into Pandas dataframe which are then saved as CSV. This part can perform analysis of individual IPL matches.
2. Pitching yorkpy.on the middle and outside off-stump to IPL – Part 2 :Class 2:This part includes functions to create a large data frame for head-to-head confrontation between any 2IPL teams says CSK-MI, DD-KKR etc, which can be saved as CSV. Analysis is then performed on these team-2-team confrontations.
3. Pitching yorkpy.swinging away from the leg stump to IPL – Part 3 Class 3:The 3rd part includes the performance of any IPL team against all other IPL teams. The data can also be saved as CSV.
4. Pitching yorkpy … in the block hole – Part 4 :Class 4: This part performs analysis of individual IPL batsmen and bowlers

Watch the live demo of the end-2-end NiFi pipeline at ‘The T20 Dance‘

You can download the NiFi template and associated code from Github at T20 Dance

The Apache NiFi Pipeline is shown below

1. T20 Dance – Overall NiFi Pipeline

There are 5 process groups

2. ListAndConvertYaml2DataFrames

This post starts with having the YAML files downloaded and unpacked from Cricsheet. The individual YAML files are converted into Pandas dataframes and saved as CSV. A concurrency of 12 is used to increase performance and process YAML files in parallel. The processor MergeContent creates a merged content to signal the completion of conversion and triggers the other Process Groups through a funnel.

3. Analyse individual IPL T20 matches

This Process Group ‘Analyse T20 matches’ used the yorkpy’s Class 1 functions which can perform analysis of individual IPL T20 matches. The matchWorm() and matchScorecard() functions are used, through any other function could have been used. The Process Group is shown below

4. Analyse performance of an IPL team in all matches against another IPL team

This Process Group ‘Analyse performance of IPL team in all matched against another IPL team‘ does analysis in all matches between any 2 IPL teams (Class 2) as shown below

5. Analyse performance of IPL team in all matches against all other IPL teams

This uses Class 3 functions. Individual data sets for each IPL team versus all other IPL teams is created before Class 3 yorkpy functions are invoked. This is included below

6. Analyse performances of IPL batsmen and bowlers

This Process Group uses Class 4 yorkpy functions. The match CSV files are processed to get batting and bowling details before calling the individual functions as shown below

7. IPL T20 Dashboard

The IPL T20 Dashboard is shown

Conclusion

This NiFI pipeline was done for IPL T20 however, it could be done for any T20 format like Intl T20, BBL, Natwest etc which are posted in Cricsheet. Also, only a subset of the yorkpy functions were used. There is a much wider variety of functions available.

Hope the T20 dance got your foot a-tapping!

To see all posts click Index of posts

Big Data-5: kNiFi-ing through cricket data with yorkpy

“The temptation to form premature theories upon insufficient data is the bane of our profession.”

Sherlock Holmes in the Valley of fear by Arthur Conan Doyle

“If we have data, let’s look at data. If all we have are opinions, let’s go with mine.”

Jim Barksdale, former CEO Netscape

In this post I use Apache NiFi Dataflow Pipeline along with my Python package yorkpy to crunch through cricket data from Cricsheet. The Data Pipelne flows all the way from the source to target analytics output. Apache NiFi was created to automate the flow of data between systems. NiFi dataflows enable the automated and managed flow of information between systems. This post automates the flow of data from Cricsheet, from where the zip file it is downloaded, unpacked, processed, transformed and finally T20 players are ranked.

While this is a straight forward example of what can be done, this pattern can be applied to real Big Data systems. For example hypothetically, we could consider that we get several parallel streams of cricket data or for that matter any sports related data. There could be parallel Data flow pipelines that get the data from the sources. This would then be followed by data transformation modules and finally a module for generating analytics. At the other end a UI based on AngularJS or ReactJS could display the results in a cool and awesome way.

Incidentally, the NiFi pipeline that I discuss in this post, is a simplistic example, and does not use the Big Data stack like HDFS, Hive, Spark etc. Nevertheless, the pattern used, has all the modules for a Big Data pipeline namely ingestion, unpacking, transformation and finally analytics. This NiF pipeline demonstrates the flow using the regular file system of Mac and my python based package yorkpy. The concepts mentioned could be used in a real Big Data scenario which has much fatter pipes of data coming. If this was the case the NiFi pipeline would utilize HDFS/Hive for storing the ingested data and Pyspark/Scala for the transformation and analytics and other related technologies.

A pictorial representation is given below

In the diagram above each of the vertical boxes could be any technology from the ever proliferating Big Data stack namely HDFS, Hive, Spark, Sqoop, Kafka, Impala and so on. Such a dataflow automation could be created when any big sporting event happens, as long as the data generated large, and there is a need for dynamic and automated reporting. The UI could be based on AngularJS/ReactJS and could display analytical tables and charts.

This post demonstrates one such scenario in which IPL T20 data is downloaded from Cricsheet site, unpacked and stored in a specific directory. This dataflow automation is based on my yorkpy package. To know more about the yorkpy package see Pitching yorkpy … short of good length to IPL – Part 1 and the associated parts. The zip file, from Cricsheet, contains individual IPL T20 matches in YAML format. The convertYaml2DataframeT20() function is used to convert the YAML files into Pandas dataframes before storing them as CSV files. After this done, the function rankIPLT20batting() function is used to perform the overall ranking of the T20 players. My yorkpy Python package has about ~ 50+ functions that perform various analytics on any T20 data for e.g it has the following classes of functions

analyze T20 matches
analyze performance of a T20 team in all matches against another T20 team
analyze performance of a T20 team against all other T20 teams
analyze performance of T20 batsman and bowlers
rank T20 batsmen and bowlers

The functions of yorkpy generate tables or charts. While this post demonstrates one scenario, we could use any of the yorkpy T20 functions, generate the output and display on a widget in the UI display, created with cool technologies like AngularJS/ReactJS, possibly in near real time as data keeps coming in.,

To use yorkpy with NiFI the following packages have to be installed in your environment

-pip install yorkpy
-pip install pyyaml
-pip install pandas
-yum install python-devel (equivalent in Windows)
-pip install matplotlib
-pip install seaborn
-pip install sklearn
-pip install datetime

I have created a video of the NiFi Pipeline with the real dataflow fro source to the ranked IPL T20 batsmen. Take a look at RankingT20PlayersWithNiFiYorkpy

You can clone/fork the NiFi template from rankT20withNiFiYorkpy

The NiFi Data Flow Automation is shown below

1. Overall flow

The overall NiFi flow contains 2 Process Groups a) DownloadAnd Unpack. b) Convert and Rank IPL batsmen. While it appears that the Process Groups are disconnected, they are not. The first process group downloads the T20 zip file, unpacks the. zip file and saves the YAML files in a specific folder. The second process group monitors this folder and starts processing as soon the YAML files are available. It processes the YAML converting it into dataframes before storing it as CSV file. The next processor then does the actual ranking of the batsmen before writing the output into IPLrank.txt

1.1 DownloadAndUnpack Process Group

This process group is shown below

1.1.1 GetT20Data

The GetT20Data Processor downloads the zip file given the URL

The ${T20data} variable points to the specific T20 format that needs to be downloaded. I have set this to https://cricsheet.org/downloads/ipl.zip. This could be set any other data set. In fact we could have parallel data flows for different T20/ Sports data sets and generate

1.1.2 SaveUnpackedData

This processor stores the YAML files in a predetermined folder, so that the data can be picked up by the 2nd Process Group for processing

1.2 ProcessAndRankT20Players Process Group

This is the second process group which converts the YAML files to pandas dataframes before storing them as. CSV files. The RankIPLPlayers will then read all the CSV files, stack them and then proceed to rank the IPL players. The Process Group is shown below

1.2.1 ListFile and FetchFile Processors

The left 2 Processors ListFile and FetchFile get all the YAML files from the folder and pass it to the next processor

1.2.2 convertYaml2DataFrame Processor

The convertYaml2DataFrame Processor uses the ExecuteStreamCommand which call a python script. The Python script invoked the yorkpy function convertYaml2Dataframe() as shown below

The ${convertYaml2Dataframe} variable points to the python file below which invoked the yorkpy function yka.convertYaml2PandasDataframeT20()

import yorkpy.analytics as yka
import argparse
parser = argparse.ArgumentParser(description='convert')
parser.add_argument("yamlFile",help="YAML File")
args=parser.parse_args()
yamlFile=args.yamlFile
yka.convertYaml2PandasDataframeT20(yamlFile,"/Users/tvganesh/backup/software/nifi/ipl","/Users/tvganesh/backup/software/nifi/ipldata")

This function takes as input $filename which comes from FetchFile processor which is a FlowFile. So I have added a concurrency of 8 to handle upto 8 Flowfiles at a time. The thumb rule as I read on the internet is 2x, 4x the number of cores of your system. Since I have an 8 core Mac, I could possibly have gone ~ 30 concurrent threads. Also the number of concurrent threads is less when the flow is run in a Oracle Box VirtualMachine. Box since a vCore < actual Core

The scheduling tab is as below

Here are the 8 concurrent Python threads on Mac at bottom right… (pretty cool!)

I have not fully tested how latency vs throughput slider changes, affects the performance.

1.2.3 MergeContent Processor

This processor’s only job is to trigger the rankIPLPlayers when all the FlowFiles have merged into 1 file.

1.2.4 RankT20Players

This processor is an ExecuteStreamCommand Processor that executes a Python script which invokes a yorkpy function rankIPLT20Batting()

import yorkpy.analytics as yka
rank=yka.rankIPLT20Batting("/Users/tvganesh/backup/software/nifi/ipldata")
print(rank.head(15))

1.2.5 OutputRankofT20Player Processor

This processor writes the generated rank to an output file.

1.3 Final Ranking of IPL T20 players

The Nodejs based web server picks up this file and displays on the web page the final ranks (the code is based on a good youtube for reading from file)

2. Final thoughts

As I have mentioned above though the above NiFi Cricket Dataflow automation does not use the Hadoop ecosystem, the pattern used is valid and can be used with some customization in Big Data flows as parallel stream. I could have also done this on Oracle VirtualBox but I thought since the code is based on Python and Pandas there is no real advantage of running on the VirtualBox. GIve the NiFi flow a shot. Have fun!!!

Also see
1.My book ‘Deep Learning from first Practical Machine Learning with R and Python – Part 5
Edition’ now on Amazon
2. Introducing QCSimulator: A 5-qubit quantum computing simulator in R
3.De-blurring revisited with Wiener filter using OpenCV
4. Practical Machine Learning with R and Python – Part 5
5. Natural language processing: What would Shakespeare say?
6.Getting started with Tensorflow, Keras in Python and R
7.Revisiting World Bank data analysis with WDI and gVisMotionChart

To see all posts click Index of posts

Rate this:

Share:

Rate this:

Share:

Rate this:

Share:

Rate this:

Share:

Rate this:

Share:

Rate this:

Share:

Display data

Create a Convolutional Neural Network

Summary of CNN

Perform Gradient descent and validate with the validation data

Generate the filter activations at the intermediate CNN layers

Display the activations at the intermediate layers

Visualize the pattern that the filters respond to maximally

Visualizing Class Outputs

Conclusion:

References

Also see

Rate this:

Share:

1. Basic Convolutional Neural Network in Tensorflow & Keras

Create CNN Model

Print model summary

Use the Adam Optimizer with binary cross entropy

Perform Gradient Descent

Plot results

2. CNN with Image Augmentation

Use Image Augumentation

Perform Gradient Descent

Plot results

Implementation using Inception Network V3

Use Inception V3

Use Layer 7 of Inception Network

Fit model

Plot results

Rate this:

Share:

1. T20 Dance – Overall NiFi Pipeline

2. ListAndConvertYaml2DataFrames

3. Analyse individual IPL T20 matches

4. Analyse performance of an IPL team in all matches against another IPL team

5. Analyse performance of IPL team in all matches against all other IPL teams

6. Analyse performances of IPL batsmen and bowlers

7. IPL T20 Dashboard

Conclusion

Rate this:

Share:

1. Overall flow

1.1 DownloadAndUnpack Process Group

1.1.1 GetT20Data

1.1.2 SaveUnpackedData

1.2 ProcessAndRankT20Players Process Group

1.2.1 ListFile and FetchFile Processors

1.2.2 convertYaml2DataFrame Processor

1.2.3 MergeContent Processor

1.2.4 RankT20Players

1.2.5 OutputRankofT20Player Processor

1.3 Final Ranking of IPL T20 players

2. Final thoughts

Rate this:

Share: