The technique of reduction of blur and restoration of images is an extremely important field of study and finds numerous applications in medical imaging and astronomy. One such technique is Wiener filter named after the originator of the technique Prof. Norbert Wiener (1894-1964). It is usually important to consider these techniques in the frequency domain.
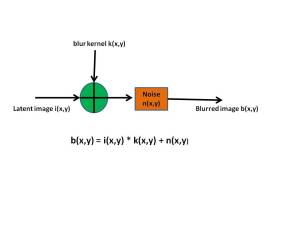
This can be represented diagrammatically as follows
Given that we have
b(x,y) = i(x,y) * k(x,y) + n(x,y) – (1)
where b(x,y) is the blurred image, i(x,y) is the latent image, k(x,y) is the blur kernel and n(x,y) is random noise.
The above in frequency domain can be written as
B(u,v) = I(u,v) * K(u,v) + N(u,v) – (2)
Inv K(u,v) represents the inverse of the blur kernel and can be determined from equation (2) by disregarding the noise. However the inverse filter has high gain at low frequencies and hence tends to amplify noise at these low frequencies.
Wiener filter and Butterworth filter try to minimize these
Wiener filter attempts to minimize the Mean Squared Error (MSE) of the following equation
e^2 = E[( i(x,y) – mean (i (x,y))^2]
The frequency domain expression for this
T(u,v) =
K*(u,v)
——– -(3)
| K(u,v)|^2 + Sn(u,v)/Sf(u,v)
Where T(u,v) is the Wiener filter
K*(u,v) is the complex conjugate of the blur kernel
|K(u,v)|^2 = k^2 + m^2 where k and m are the coefficients of the real and imaginary parts of the blur kernel
Sn(u,v) is the power spectra of noise
Sf(u,v) is the power spectra of the signal
Equation (3) can be represented as
T(u,v) =
K*(u,v)
——– – (4)
| K(u,v)|^2 + L
Where L is a small positive value
Eqn(4) represents Wiener filter
The lecture “Image deblurring by Frequency Domain Operations” by Prof. Harvey Rhody is worth a read.
One thing that puzzles me is the Wiener filter is the inverse of the blur kernel with the additional factor of ‘L’ in the denominator. The contribution of the factor ‘L’ will be small, so the Wiener filter appears to be the same as a regular inverse filter. I am probably missing something here(??).
You can clone the code below from Git Hub – Weiner filter with OpenCV
The steps to create the Wiener filter were as follow
1. Create the gray image of the blurred original

2. Add additive noise to the blurred original
// Add the random noise matric to the image cvAdd(im,&noise,im, 0); 3.Gaussian smooth the noisy blurred image cvSmooth( im, im, CV_GAUSSIAN, 7, 7, 0.5, 0.5 );4.Perform DFT and inverse DFT (to check) of the original image (noisy, blurred image) // Perform DFT of original image dft_A = cvShowDFT1(im, dft_M1, dft_N1,"original"); //Perform inverse (check) cvShowInvDFT1(im,dft_A,dft_M1,dft_N1, "original");
5.Perform DFT and inverse DFT of blur kernel // Perform DFT of kernel dft_B = cvShowDFT1(k_image,dft_M1,dft_N1,"kernel"); //Perform inverse of kernel (check) cvShowInvDFT1(k_image,dft_B,dft_M1,dft_N1, "kernel");
6.Multiply DFT of original with complex conjugate of blur kernel // Multiply numerator with complex conjugate dft_C = cvCreateMat( dft_M1, dft_N1, CV_64FC2 ); 7.Calculate modulus of blur kernel (denominator) // Split Real and imaginary parts cvSplit( dft_B, image_ReB, image_ImB, 0, 0 ); cvPow( image_ReB, image_ReB, 2.0); cvPow( image_ImB, image_ImB, 2.0); cvAdd(image_ReB, image_ImB, image_ReB,0); 8.Add Wiener constant to modulus of blur kernel (denominator) val = cvScalarAll(0.00001); cvAddS(image_ReB,val,image_ReB,0); 9.Divide the numerator with the denominator //Divide Numerator/A^2 + B^2 cvDiv(image_ReC, image_ReB, image_ReC, 1.0); cvDiv(image_ImC, image_ReB, image_ImC, 1.0); 10.Perform inverse DFT of the filtered signal
// Perform Inverse
cvShowInvDFT1(im, (CvMat *)complex_ImC,dft_M1,dft_N1,"Output - Wiener filter");
There is still a residual amount of blur (do also read De-blurring revisited with Wiener filter using OpenCV). This can be tried for different values of the Wiener introduced noise.
Note: I would like to give special thanks to Egli Simon who identified the bug in my previous version of the code. The line to display the inverse DFT of the original image & the blur kernel overwrote the DFT contents and I was not getting the Wiener filter to work
Note: You can clone the code below from Git Hub – Weiner filter with OpenCV
The complete code is given below (re-worked and should work as is)
/*
============================================================================
Name : wiener1.c
Author : Tinniam V Ganesh & Egli Simon
Version :
Copyright :
Description : Wiener filter implementation in OpenCV (22 Nov 2011)
============================================================================
*/
#include <stdio.h>
#include <stdlib.h>
#include “cxcore.h”
#include “cv.h”
#include “highgui.h”
#define kappa 1
#define rad 2
int main(int argc, char ** argv)
{
int height,width,step,channels,depth;
uchar* data1;
CvMat *dft_A;
CvMat *dft_B;
CvMat *dft_C;
IplImage* im;
IplImage* im1;
IplImage* image_ReB;
IplImage* image_ImB;
IplImage* image_ReC;
IplImage* image_ImC;
IplImage* complex_ImC;
CvScalar val;
IplImage* k_image_hdr;
int i,j,k;
FILE *fp;
fp = fopen(“test.txt”,”w+”);
int dft_M,dft_N;
int dft_M1,dft_N1;
CvMat* cvShowDFT1(IplImage*, int, int,char*);
void cvShowInvDFT1(IplImage*, CvMat*, int, int,char*);
im1 = cvLoadImage( “kutty-1.jpg”,1 );
cvNamedWindow(“Original-color”, 0);
cvShowImage(“Original-color”, im1);
im = cvLoadImage( “kutty-1.jpg”, CV_LOAD_IMAGE_GRAYSCALE );
if( !im )
return -1;
cvNamedWindow(“Original-gray”, 0);
cvShowImage(“Original-gray”, im);
// Create a random noise matrix
fp = fopen(“test.txt”,”w+”);
int val_noise[357*383];
for(i=0; i <im->height;i++){
for(j=0;j<im->width;j++){
fprintf(fp, “%d “,(383*i+j));
val_noise[383*i+j] = rand() % 128;
}
fprintf(fp, “\n”);
}
CvMat noise = cvMat(im->height,im->width, CV_8UC1,val_noise);
// Add the random noise matric to the image
cvAdd(im,&noise,im, 0);
cvNamedWindow(“Original + Noise”, 0);
cvShowImage(“Original + Noise”, im);
cvSmooth( im, im, CV_GAUSSIAN, 7, 7, 0.5, 0.5 );
cvNamedWindow(“Gaussian Smooth”, 0);
cvShowImage(“Gaussian Smooth”, im);
// Create a blur kernel
IplImage* k_image;
float r = rad;
float radius=((int)(r)*2+1)/2.0;
int rowLength=(int)(2*radius);
printf(“rowlength %d\n”,rowLength);
float kernels[rowLength*rowLength];
printf(“rowl: %i”,rowLength);
int norm=0; //Normalization factor
int x,y;
CvMat kernel;
for(x = 0; x < rowLength; x++)
for (y = 0; y < rowLength; y++)
if (sqrt((x – (int)(radius) ) * (x – (int)(radius) ) + (y – (int)(radius))* (y – (int)(radius))) <= (int)(radius))
norm++;
// Populate matrix
for (y = 0; y < rowLength; y++) //populate array with values
{
for (x = 0; x < rowLength; x++) {
if (sqrt((x – (int)(radius) ) * (x – (int)(radius) ) + (y – (int)(radius))
* (y – (int)(radius))) <= (int)(radius)) {
//kernels[y * rowLength + x] = 255;
kernels[y * rowLength + x] =1.0/norm;
printf(“%f “,1.0/norm);
}
else{
kernels[y * rowLength + x] =0;
}
}
}
/*for (i=0; i < rowLength; i++){
for(j=0;j < rowLength;j++){
printf(“%f “, kernels[i*rowLength +j]);
}
}*/
kernel= cvMat(rowLength, // number of rows
rowLength, // number of columns
CV_32FC1, // matrix data type
&kernels);
k_image_hdr = cvCreateImageHeader( cvSize(rowLength,rowLength), IPL_DEPTH_32F,1);
k_image = cvGetImage(&kernel,k_image_hdr);
height = k_image->height;
width = k_image->width;
step = k_image->widthStep/sizeof(float);
depth = k_image->depth;
channels = k_image->nChannels;
//data1 = (float *)(k_image->imageData);
data1 = (uchar *)(k_image->imageData);
cvNamedWindow(“blur kernel”, 0);
cvShowImage(“blur kernel”, k_image);
dft_M = cvGetOptimalDFTSize( im->height – 1 );
dft_N = cvGetOptimalDFTSize( im->width – 1 );
//dft_M1 = cvGetOptimalDFTSize( im->height+99 – 1 );
//dft_N1 = cvGetOptimalDFTSize( im->width+99 – 1 );
dft_M1 = cvGetOptimalDFTSize( im->height+3 – 1 );
dft_N1 = cvGetOptimalDFTSize( im->width+3 – 1 );
printf(“dft_N1=%d,dft_M1=%d\n”,dft_N1,dft_M1);
// Perform DFT of original image
dft_A = cvShowDFT1(im, dft_M1, dft_N1,”original”);
//Perform inverse (check)
//cvShowInvDFT1(im,dft_A,dft_M1,dft_N1, “original”); – Commented as it overwrites the DFT
// Perform DFT of kernel
dft_B = cvShowDFT1(k_image,dft_M1,dft_N1,”kernel”);
//Perform inverse of kernel (check)
//cvShowInvDFT1(k_image,dft_B,dft_M1,dft_N1, “kernel”);- Commented as it overwrites the DFT
// Multiply numerator with complex conjugate
dft_C = cvCreateMat( dft_M1, dft_N1, CV_64FC2 );
printf(“%d %d %d %d\n”,dft_M,dft_N,dft_M1,dft_N1);
// Multiply DFT(blurred image) * complex conjugate of blur kernel
cvMulSpectrums(dft_A,dft_B,dft_C,CV_DXT_MUL_CONJ);
//cvShowInvDFT1(im,dft_C,dft_M1,dft_N1,”blur1″);
// Split Fourier in real and imaginary parts
image_ReC = cvCreateImage( cvSize(dft_N1, dft_M1), IPL_DEPTH_64F, 1);
image_ImC = cvCreateImage( cvSize(dft_N1, dft_M1), IPL_DEPTH_64F, 1);
complex_ImC = cvCreateImage( cvSize(dft_N1, dft_M1), IPL_DEPTH_64F, 2);
printf(“%d %d %d %d\n”,dft_M,dft_N,dft_M1,dft_N1);
//cvSplit( dft_C, image_ReC, image_ImC, 0, 0 );
cvSplit( dft_C, image_ReC, image_ImC, 0, 0 );
// Compute A^2 + B^2 of denominator or blur kernel
image_ReB = cvCreateImage( cvSize(dft_N1, dft_M1), IPL_DEPTH_64F, 1);
image_ImB = cvCreateImage( cvSize(dft_N1, dft_M1), IPL_DEPTH_64F, 1);
// Split Real and imaginary parts
cvSplit( dft_B, image_ReB, image_ImB, 0, 0 );
cvPow( image_ReB, image_ReB, 2.0);
cvPow( image_ImB, image_ImB, 2.0);
cvAdd(image_ReB, image_ImB, image_ReB,0);
val = cvScalarAll(kappa);
cvAddS(image_ReB,val,image_ReB,0);
//Divide Numerator/A^2 + B^2
cvDiv(image_ReC, image_ReB, image_ReC, 1.0);
cvDiv(image_ImC, image_ReB, image_ImC, 1.0);
// Merge Real and complex parts
cvMerge(image_ReC, image_ImC, NULL, NULL, complex_ImC);
// Perform Inverse
cvShowInvDFT1(im, (CvMat *)complex_ImC,dft_M1,dft_N1,”O/p Wiener k=1 rad=2″);
cvWaitKey(-1);
return 0;
}
CvMat* cvShowDFT1(IplImage* im, int dft_M, int dft_N,char* src)
{
IplImage* realInput;
IplImage* imaginaryInput;
IplImage* complexInput;
CvMat* dft_A, tmp;
IplImage* image_Re;
IplImage* image_Im;
char str[80];
double m, M;
realInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 1);
imaginaryInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 1);
complexInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 2);
cvScale(im, realInput, 1.0, 0.0);
cvZero(imaginaryInput);
cvMerge(realInput, imaginaryInput, NULL, NULL, complexInput);
dft_A = cvCreateMat( dft_M, dft_N, CV_64FC2 );
image_Re = cvCreateImage( cvSize(dft_N, dft_M), IPL_DEPTH_64F, 1);
image_Im = cvCreateImage( cvSize(dft_N, dft_M), IPL_DEPTH_64F, 1);
// copy A to dft_A and pad dft_A with zeros
cvGetSubRect( dft_A, &tmp, cvRect(0,0, im->width, im->height));
cvCopy( complexInput, &tmp, NULL );
if( dft_A->cols > im->width )
{
cvGetSubRect( dft_A, &tmp, cvRect(im->width,0, dft_A->cols – im->width, im->height));
cvZero( &tmp );
}
// no need to pad bottom part of dft_A with zeros because of
// use nonzero_rows parameter in cvDFT() call below
cvDFT( dft_A, dft_A, CV_DXT_FORWARD, complexInput->height );
strcpy(str,”DFT -“);
strcat(str,src);
cvNamedWindow(str, 0);
// Split Fourier in real and imaginary parts
cvSplit( dft_A, image_Re, image_Im, 0, 0 );
// Compute the magnitude of the spectrum Mag = sqrt(Re^2 + Im^2)
cvPow( image_Re, image_Re, 2.0);
cvPow( image_Im, image_Im, 2.0);
cvAdd( image_Re, image_Im, image_Re, NULL);
cvPow( image_Re, image_Re, 0.5 );
// Compute log(1 + Mag)
cvAddS( image_Re, cvScalarAll(1.0), image_Re, NULL ); // 1 + Mag
cvLog( image_Re, image_Re ); // log(1 + Mag)
cvMinMaxLoc(image_Re, &m, &M, NULL, NULL, NULL);
cvScale(image_Re, image_Re, 1.0/(M-m), 1.0*(-m)/(M-m));
cvShowImage(str, image_Re);
return(dft_A);
}
void cvShowInvDFT1(IplImage* im, CvMat* dft_A, int dft_M, int dft_N,char* src)
{
IplImage* realInput;
IplImage* imaginaryInput;
IplImage* complexInput;
IplImage * image_Re;
IplImage * image_Im;
double m, M;
char str[80];
realInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 1);
imaginaryInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 1);
complexInput = cvCreateImage( cvGetSize(im), IPL_DEPTH_64F, 2);
image_Re = cvCreateImage( cvSize(dft_N, dft_M), IPL_DEPTH_64F, 1);
image_Im = cvCreateImage( cvSize(dft_N, dft_M), IPL_DEPTH_64F, 1);
//cvDFT( dft_A, dft_A, CV_DXT_INV_SCALE, complexInput->height );
cvDFT( dft_A, dft_A, CV_DXT_INV_SCALE, dft_M);
strcpy(str,”DFT INVERSE – “);
strcat(str,src);
cvNamedWindow(str, 0);
// Split Fourier in real and imaginary parts
cvSplit( dft_A, image_Re, image_Im, 0, 0 );
// Compute the magnitude of the spectrum Mag = sqrt(Re^2 + Im^2)
cvPow( image_Re, image_Re, 2.0);
cvPow( image_Im, image_Im, 2.0);
cvAdd( image_Re, image_Im, image_Re, NULL);
cvPow( image_Re, image_Re, 0.5 );
// Compute log(1 + Mag)
cvAddS( image_Re, cvScalarAll(1.0), image_Re, NULL ); // 1 + Mag
cvLog( image_Re, image_Re ); // log(1 + Mag)
cvMinMaxLoc(image_Re, &m, &M, NULL, NULL, NULL);
cvScale(image_Re, image_Re, 1.0/(M-m), 1.0*(-m)/(M-m));
//cvCvtColor(image_Re, image_Re, CV_GRAY2RGBA);
cvShowImage(str, image_Re);
}
 Checkout my book ‘Deep Learning from first principles Second Edition- In vectorized Python, R and Octave’. My book is available on Amazon as paperback ($18.99) and in kindle version($9.99/Rs449).
Checkout my book ‘Deep Learning from first principles Second Edition- In vectorized Python, R and Octave’. My book is available on Amazon as paperback ($18.99) and in kindle version($9.99/Rs449).
You may also like my companion book “Practical Machine Learning with R and Python:Second Edition- Machine Learning in stereo” available in Amazon in paperback($12.99) and Kindle($9.99/Rs449) versions.
See also
– Experiments with deblurring using OpenCV
– Dabbling with Wiener filter using OpenCV
– Deblurring with OpenCV: Wiener filter reloaded
– Re-working the Lucy-Richardson Algorithm in OpenCV
Find me on Google+


I’m not sure if you are aware of it, but the code you posted surely doesn’t work as is:
when you’re showing the inverse dft you’re also changing the content of the array you’re showing, this leads to you multiplying the image in the time domain, not frequency domain.
I basically have the same code as you (copied and modified to my purpose), and it seems to work.
Mail me if you want my (actually your) working code.
Regards, Simon
LikeLike
Simon, I posted the code and the output from this program only. I did finally make some cosmetic changes and probably accidentally deleted some line. Will check and re-post again. Do drop me a mail and let me know where I went wrong! Thanks a million!
LikeLike
hello can I have a copy of that code? I’m currently doing a study on the wiener filter
LikeLike
Miko, The entire code is in the blog post. Feel free to use it as you please. Also look at my other post, Deblurring with Wiener filter using OpenCV. The code should work as is on Linux/Windows.
LikeLike
Simon, Thanks for pointing out the bug was because of displaying the inverse DFT of the original image and the kernel which was overwriting the array contents. I have commented out these lines and have also included your blur kernel. Now the code should work as is…
LikeLike
Why outpu image is way brighter than input image? Maybe output should be normalized?
LikeLike
Hi sir,
Can we get this code using python?
LikeLike
I have not implemented in Python. You are free to do so.
LikeLike