Cricketr analyzes Ind-Aus faceoff in WTC 2023!!

“The unexamined life is not worth living.” – Socrates

“There is no easy way from the earth to the stars.” – Seneca

“If you want to go fast, go alone. If you want to go far, go together.” – African Proverb

1. Introduction

In this post, I put my R package cricketr to analyze the Indian and Australia World Test Championship (WTC) final squad ahead of the World Test Championship 2023.My R package cricketr had its birth on Jul 4, 2015. Cricketr uses data from Cricinfo.

You can download the latest PDF version of the book at ‘Cricket analytics with cricketr and cricpy: Analytics harmony with R and Python-6th edition‘

Indian squad

Rohit Sharma (Captain), Shubman Gill, Cheteshwar Pujara, Virat Kohli, Ajinkya Rahane, Ravindra Jadeja, Shardul Thakur, Mohd. Shami, Mohd. Siraj, Ishan Kishan (wk).

According to me, Ishan Kishan has more experience than KS Bharat, though Rishabh Pant would have been the ideal wicket keeper/left-handed batsman. I think Shardul Thakur would be handful in the English conditions. For a spinner it either Ashwin or Jadeja. Maybe the balance shifts in favor of Jadeja

Australian squad

Pat Cummins (capt), Alex Carey (wk), Cameron Green, Josh Hazlewood, Usman Khawaja, Marnus Labuschagne, Nathan Lyon, Todd Murphy, Steven Smith (vice-capt), Mitchell Starc, David Warner.

Not sure if Scott Boland would fill in, instead of Todd Murphy 1

Let me give you a lay-of-the-land (post) below

The post below is organized into the following parts

Analysis of Indian WTC batsmen from Jan 2016 – May 2023
Analysis of Indian WTC batsmen against Australia from Jan 2016 -May 2023
Analysis of Australian WTC batsmen from Jan 2016 – May 2023
Analysis of Australian WTC batsmen against India from Jan 2016 -May 2023
Analysis of Indian WTC bowlers from Jan 2016 – May 2023
Analysis of Indian WTC bowlers against Australia from Jan 2016 -May 2023
Analysis of Australian WTC bowlers from Jan 2016 – May 2023
Analysis of Australian WTC bowlers gainst India from Jan 2016 -May 2023
Team analysis of India and Australia

All the above analysis use data from ESPN Statsguru and use my R pakage cricketr

The data for the different players have been obtained using calls such as the ones below.

# Get Shubman Gill's batting data
#shubman <-getPlayerData(1070173,dir=".",file="shubman.csv",type="batting",homeOrAway=c(1,2), result=c(1,2,4))
#shubmansp <- getPlayerDataSp(1070173,tdir=".",tfile="shubmansp.csv",ttype="batting")

#Get Shubman Gill's data from Jan 2016 - May 2023
#df <-getPlayerDataHA(1070173,tfile="shubman1.csv",type="batting", matchType="Test")
#df1=getPlayerDataOppnHA(infile="shubman1.csv",outfile="shubmanTestAus.csv",startDate="2016-01-01",endDate="2023-05-01")

#Get Shubman Gills data from Jan 2016 - May 2023, against Australia
#df <-getPlayerDataHA(1070173,tfile="shubman1.csv",type="batting", matchType="Test")
#df1=getPlayerDataOppnHA(infile="shubman1.csv",outfile="shubmanTestAus.csv",opposition="Australia",startDate="2016-01-01",endDate="2023-05-01")

Note: To get data for bowlers we need to use the corresponding profile no and use type =‘bowling’. Details in my posts below

To do similar analysis please go through the following posts

Note 1: I will not be analysing each and every chart as the charts are quite self-explanatory

Note 2: I have had to tile charts together otherwise this will become a very, very long post. You are free to use my R package cricketr and check out for yourself ##3. Analysis of India WTC batsmen from Jan 2016 – May 2023

Findings

Kohli has the best average of 48+. India has won when Rohit and Rahane played well
Kohli’s tops the list in cumulative average runs, followed by Pujara and Rohit is 3rd. Gill is on the upswing.
Against Australia Pujara has the best cumulative average runs record followed by Rahane, with Gill in hot pursuit. In the strike rate department Gill tops followed by Rohit and Rahane
Since 2016 Smith, Labuschagne has an average of 53+ since 2016!! Warner & Khwaja are at ~46
Australia has won matches when Smith, Warner and Khwaja have played well.
Labuschagne, Smith and C Green have good records against India. Indian bowlers will need to contain them
Ashwin has the highest wickets followed by Jadeja against all teams. Ashwin’s performance has dropped over the years, while Siraj has been becoming better
Jadeja has the best economy rate followed by Ashwin
Against Australia specifically Jadeja has the best record followed by Ashwin. Jadeja has the best economy against Australia, followed by Siraj, then Ashwin
Cummins, Starc and Lyons are the best performers for Australia. Hazzlewood, Cummins have the best economy against all opposition
Against India Lyon, Cummins and Hazzlewood have performed well
Hazzlewood, Lyon have a good economy rate against India
Against Australia India has won 17 times, lost 60 and drawn 22 in Australia. At home India won 42, tied 2, lost 28 and drawn 24
At the Oval where the World Test Championship is going to be held India has won 4, lost 10 and drawn 10.

Note 3: You can also read this post at Rpubs at ind-aus-WTC !! The formatting will be nicer!

Note 4: You can download this post as PDF to read at your leisure ind-aus-WTC.pdf

2. Install the cricketr package

if (!require("cricketr")){
    install.packages("cricketr",lib = "c:/test")
}
library(cricketr)

3a. Basic analysis

The analyses below include – Runs frequency plot – Mean strike rate – Run Ranges

Kohli’s strike rate increases with increasing runs, while Gill’s seems to drop. So it is with Pujara & Rahane

par(mfrow=c(3,3))
par(mar=c(4,4,2,2))
batsmanRunsFreqPerf("kohliTest.csv","Kohli")
batsmanMeanStrikeRate("kohliTest.csv","Kohli")
batsmanRunsRanges("kohliTest.csv","Kohli")

batsmanRunsFreqPerf("rohitTest.csv","Rohit")
batsmanMeanStrikeRate("rohitTest.csv","Rohit")
batsmanRunsRanges("rohitTest.csv","Rohit")

batsmanRunsFreqPerf("shubmanTest.csv","S Gill")
batsmanMeanStrikeRate("shubmanTest.csv","S Gill")
batsmanRunsRanges("shubmanTest.csv","S Gill")

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))
batsmanRunsFreqPerf("rahaneTest.csv","Rahane")
batsmanMeanStrikeRate("rahaneTest.csv","Rahane")
batsmanRunsRanges("rahaneTest.csv","Rahane")

batsmanRunsFreqPerf("pujaraTest.csv","Pujara")
batsmanMeanStrikeRate("pujaraTest.csv","Pujara")
batsmanRunsRanges("pujaraTest.csv","Pujara")

3b. More analyses

Kohli hits roughly 5 4s in his 50 versus Gill,Pujara who is able to smash 6 4s.

par(mfrow=c(3,3))
par(mar=c(4,4,2,2))

batsman4s("kohliTest.csv","Kohli")
batsman6s("kohliTest.csv","Kohli")
batsmanMeanStrikeRate("kohliTest.csv","Kohli")

batsman4s("rohitTest.csv","Rohit")
batsman6s("rohitTest.csv","Rohit")
batsmanMeanStrikeRate("rohitTest.csv","Rohit")

batsman4s("shubmanTest.csv","S Gill")
batsman6s("shubmanTest.csv","S Gill")
batsmanMeanStrikeRate("shubmanTest.csv","S Gill")

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

batsman4s("rahaneTest.csv","Rahane")
batsman6s("rahaneTest.csv","Rahane")
batsmanMeanStrikeRate("rahane.csv","Rahane")

batsman4s("pujaraTest.csv","Pujara")
batsman6s("pujaraTest.csv","Pujara")
batsmanMeanStrikeRate("pujaraTest.csv","Pujara")

3c.Boxplot histogram plot

This plot shows a combined boxplot of the Runs ranges and a histog2ram of the Runs Frequency Kohli’s average is 48, while Rohit,Pujara is 40 with Rahane and Gill around 33.

batsmanPerfBoxHist("kohliTest.csv","Kohli")

batsmanPerfBoxHist("rohitTest.csv","Rohit")

batsmanPerfBoxHist("shubmanTest.csv","S Gill")

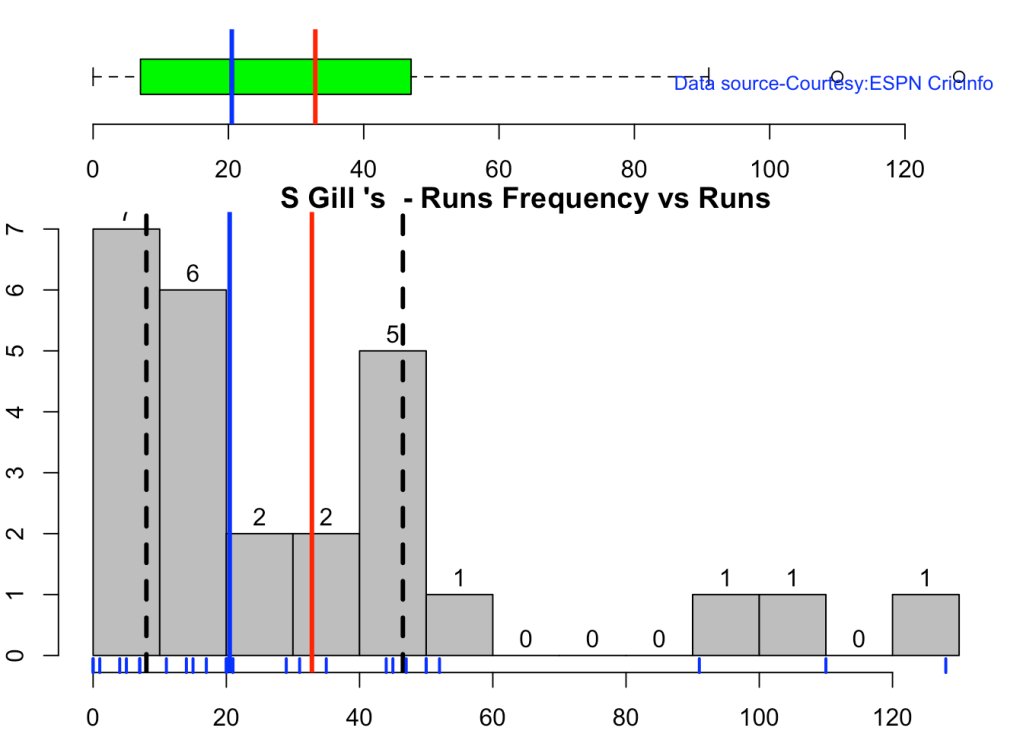
batsmanPerfBoxHist("rahaneTest.csv","Rahane")

batsmanPerfBoxHist("pujaraTest.csv","Pujara")

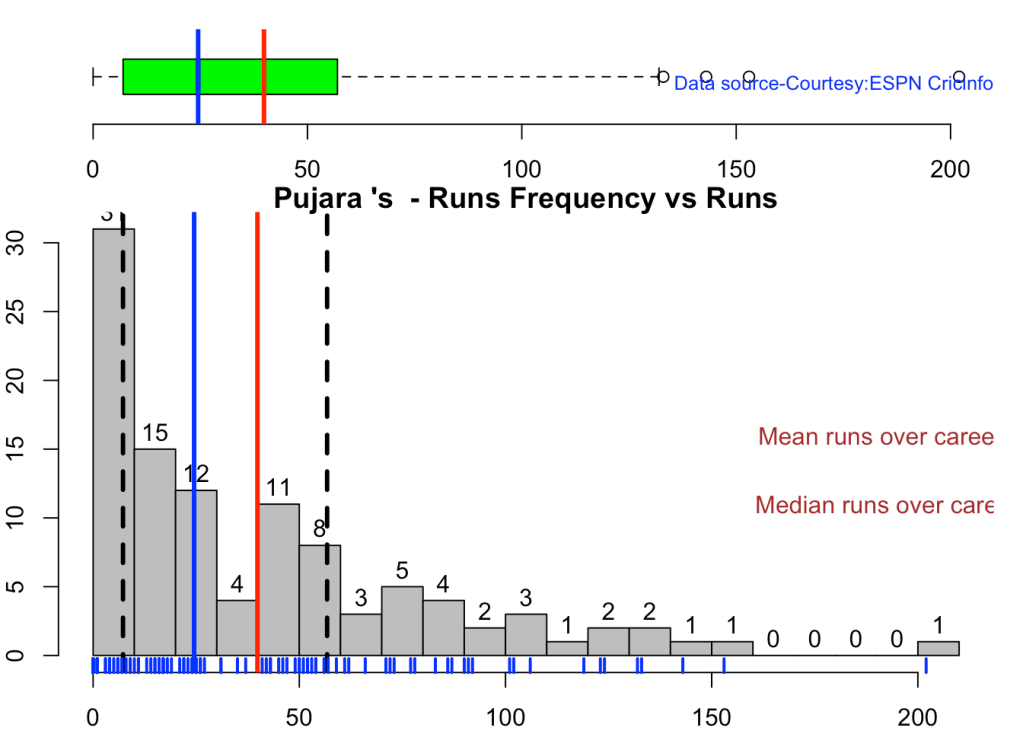
3d. Contribution to won and lost matches

For the functions below you will have to use the getPlayerDataSp() function. When Rohit Sharma and Pujara have played well India have tended to win more often

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanContributionWonLost("kohlisp.csv","Kohli")
batsmanContributionWonLost("rohitsp.csv","Rohit")
batsmanContributionWonLost("rahanesp.csv","Rahane")
batsmanContributionWonLost("pujarasp.csv","Pujara")

3e. Performance at home and overseas

This function also requires the use of getPlayerDataSp() as shown above. This can only be used for Test matches

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanPerfHomeAway("kohlisp.csv","Kohli")
batsmanPerfHomeAway("rohitsp.csv","Rohit")
batsmanPerfHomeAway("rahanesp.csv","Rahane")
batsmanPerfHomeAway("pujarasp.csv","Pujara")

3f. Batsman average at different venues

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanAvgRunsGround("kohliTest.csv","Kohli")
batsmanAvgRunsGround("rohitTest.csv","Rohit")
batsmanAvgRunsGround("rahaneTest.csv","Rahane")
batsmanAvgRunsGround("pujaraTest.csv","Pujara")

3g. Batsman average against different opposition

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanAvgRunsOpposition("kohliTest.csv","Kohli")
batsmanAvgRunsOpposition("rohitTest.csv","Rohit")
batsmanAvgRunsOpposition("rahaneTest.csv","Rahane")
batsmanAvgRunsOpposition("pujaraTest.csv","Pujara")

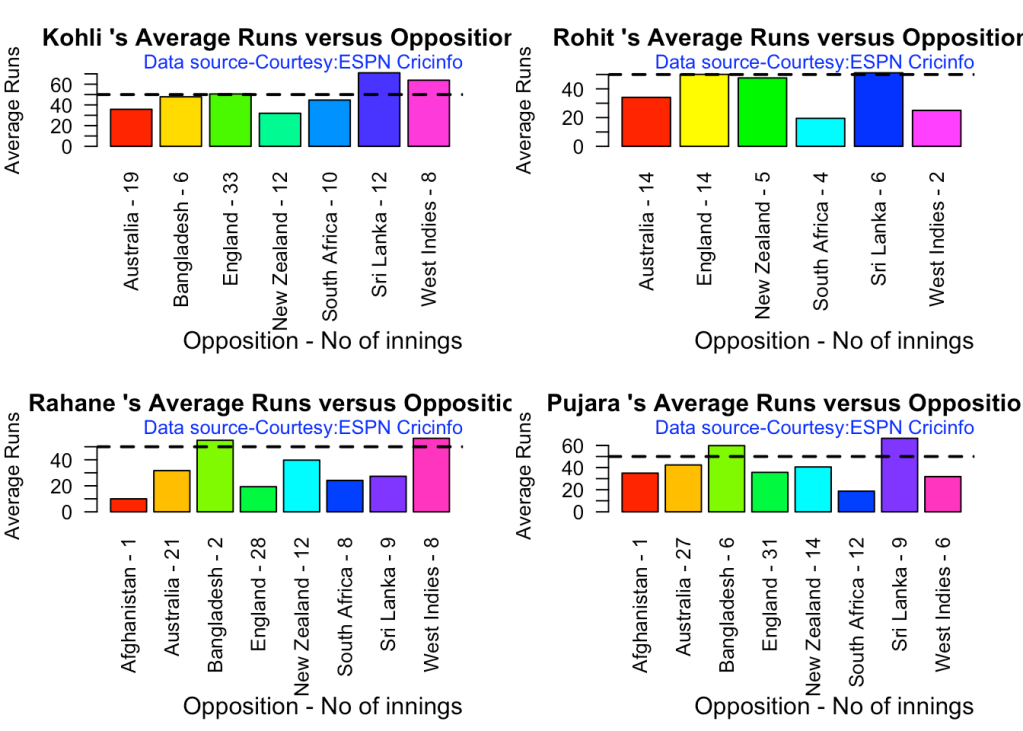
3h. Runs Likelihood of batsman

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanRunsLikelihood("kohli.csv","Kohli")

## Summary of  Kohli 's runs scoring likelihood
## **************************************************
## 
## There is a 52.91 % likelihood that Kohli  will make  12 Runs in  26 balls over 35  Minutes 
## There is a 30.81 % likelihood that Kohli  will make  52 Runs in  100 balls over  139  Minutes 
## There is a 16.28 % likelihood that Kohli  will make  142 Runs in  237 balls over 335  Minutes

batsmanRunsLikelihood("rohit.csv","Rohit")

## Summary of  Rohit 's runs scoring likelihood
## **************************************************
## 
## There is a 43.24 % likelihood that Rohit  will make  10 Runs in  21 balls over 32  Minutes 
## There is a 45.95 % likelihood that Rohit  will make  46 Runs in  85 balls over  124  Minutes 
## There is a 10.81 % likelihood that Rohit  will make  110 Runs in  199 balls over 282  Minutes

batsmanRunsLikelihood("rahane.csv","Rahane")

## Summary of  Rahane 's runs scoring likelihood
## **************************************************
## 
## There is a 7.75 % likelihood that Rahane  will make  124 Runs in  224 balls over 318  Minutes 
## There is a 62.02 % likelihood that Rahane  will make  12 Runs in  26 balls over  37  Minutes 
## There is a 30.23 % likelihood that Rahane  will make  55 Runs in  113 balls over 162  Minutes

batsmanRunsLikelihood("pujara.csv","Pujara")

## Summary of  Pujara 's runs scoring likelihood
## **************************************************
## 
## There is a 60.49 % likelihood that Pujara  will make  15 Runs in  38 balls over 55  Minutes 
## There is a 31.48 % likelihood that Pujara  will make  62 Runs in  142 balls over  204  Minutes 
## There is a 8.02 % likelihood that Pujara  will make  153 Runs in  319 balls over 445  Minutes

3h1. Moving average of batsman

Kohli’s moving average in tests seem to havw dropped after a peak in 2017, 2018. So it is with Rahane

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanMovingAverage("kohli.csv","Kohli")
batsmanMovingAverage("rohit.csv","Rohit")
batsmanMovingAverage("rahane.csv","Rahane")
batsmanMovingAverage("pujara.csv","Pujara")

3i. Cumulative Average runs of batsman in career

Kohli’s cumulative average averages to ~48. Shubman Gill’s cumulative average is on the rise.

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanCumulativeAverageRuns("kohliTest.csv","Kohli")

batsmanCumulativeAverageRuns("rohitTest.csv","Rohit")

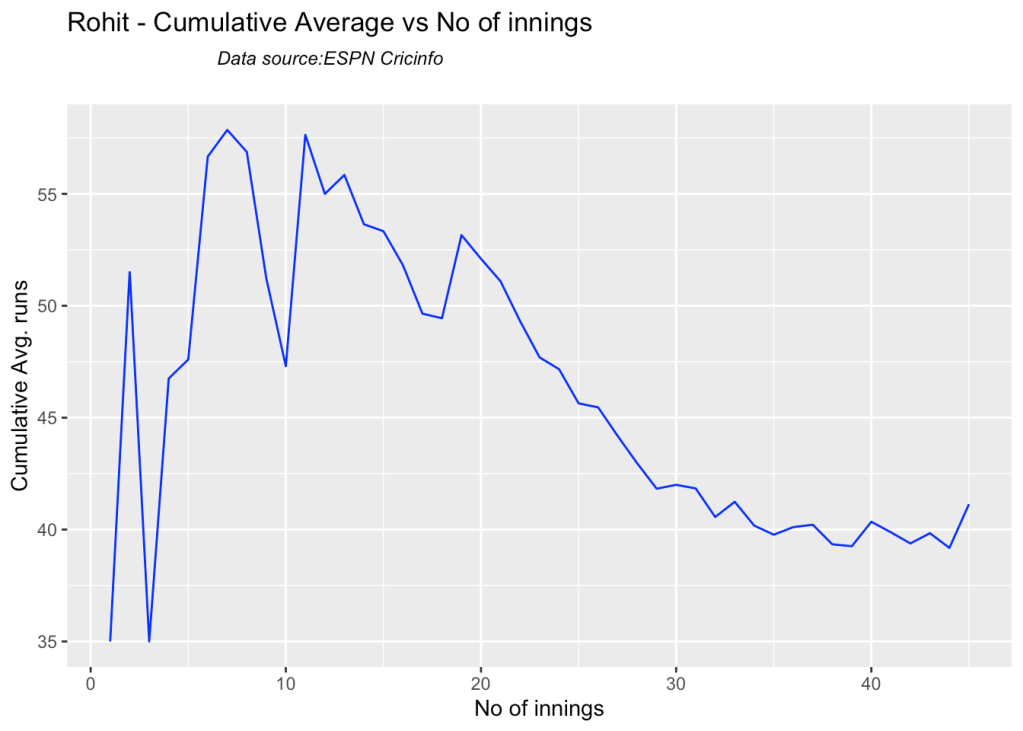
batsmanCumulativeAverageRuns("rahaneTest.csv","Rahane")

batsmanCumulativeAverageRuns("pujaraTest.csv","Pujara")

batsmanCumulativeAverageRuns("shubmanTest.csv","S Gill")

3j Cumulative Average strike rate of batsman in career

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanCumulativeStrikeRate("kohliTest.csv","Kohli")

batsmanCumulativeStrikeRate("rohitTest.csv","Rohit")

batsmanCumulativeStrikeRate("rahaneTest.csv","Rahane")

batsmanCumulativeStrikeRate("pujaraTest.csv","Pujara")

batsmanCumulativeStrikeRate("shubmanTest.csv","S Gill")

3k. Future Runs forecast

Here are plots that forecast how the batsman will perform in future. In this case 90% of the career runs trend is uses as the training set. the remaining 10% is the test set.

A Holt-Winters forecating model is used to forecast future performance based on the 90% training set. The forecated runs trend is plotted. The test set is also plotted to see how close the forecast and the actual matches

Take a look at the runs forecasted for the batsman below.

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanPerfForecast("kohli.csv","Kohli")
batsmanPerfForecast("rohit.csv","Rohit")
batsmanPerfForecast("rahane.csv","Rahane")
batsmanPerfForecast("pujara.csv","Pujara")

3l. Relative Mean Strike Rate plot

The plot below compares the Mean Strike Rate of the batsman for each of the runs ranges of 10 and plots them. The plot indicate the following

frames <- list("kohliTest.csv","rohitTest.csv","pujaraTest.csv","rahaneTest.csv","shubmanTest.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeBatsmanSR(frames,names)

3m. Relative Runs Frequency plot

The plot below gives the relative Runs Frequency Percetages for each 10 run bucket. The plot below show

frames <- list("kohliTest.csv","rohitTest.csv","pujaraTest.csv","rahaneTest.csv","shubmanTest.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeRunsFreqPerf(frames,names)

3n. Relative cumulative average runs in career

Kohli’s tops the list, followed by Pujara and Rohit is 3rd. Gill is on the upswing. Hope he performs well.

frames <- list("kohliTest.csv","rohitTest.csv","pujaraTest.csv","rahaneTest.csv","shubmanTest.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeBatsmanCumulativeAvgRuns(frames,names)

3o. Relative cumulative average strike rate in career

ROhit has the best strike rate followed by Kohli, with Shubman Gill ctaching up fast

frames <- list("kohliTest.csv","rohitTest.csv","pujaraTest.csv","rahaneTest.csv","shubmanTest.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeBatsmanCumulativeStrikeRate(frames,names)

3p. Check Batsman In-Form or Out-of-Form

The below computation uses Null Hypothesis testing and p-value to determine if the batsman is in-form or out-of-form. For this 90% of the career runs is chosen as the population and the mean computed. The last 10% is chosen to be the sample set and the sample Mean and the sample Standard Deviation are caculated.

The Null Hypothesis (H0) assumes that the batsman continues to stay in-form where the sample mean is within 95% confidence interval of population mean The Alternative (Ha) assumes that the batsman is out of form the sample mean is beyond the 95% confidence interval of the population mean.

A significance value of 0.05 is chosen and p-value us computed If p-value >= .05 – Batsman In-Form If p-value < 0.05 – Batsman Out-of-Form

Note Ideally the p-value should be done for a population that follows the Normal Distribution. But the runs population is usually left skewed. So some correction may be needed. I will revisit this later

This is done for the Top 4 batsman

checkBatsmanInForm("kohli.csv","Kohli")

## [1] "**************************** Form status of Kohli ****************************\n\n Population size: 154  Mean of population: 47.03 \n Sample size: 18  Mean of sample: 32.22 SD of sample: 42.45 \n\n Null hypothesis H0 : Kohli 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Kohli 's sample average is below the 95% confidence interval of population average\n\n Kohli 's Form Status: In-Form because the p value: 0.078058  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("rohit.csv","Rohit")

## [1] "**************************** Form status of Rohit ****************************\n\n Population size: 66  Mean of population: 37.03 \n Sample size: 8  Mean of sample: 37.88 SD of sample: 35.38 \n\n Null hypothesis H0 : Rohit 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Rohit 's sample average is below the 95% confidence interval of population average\n\n Rohit 's Form Status: In-Form because the p value: 0.526254  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("rahane.csv","Rahane")

## [1] "**************************** Form status of Rahane ****************************\n\n Population size: 116  Mean of population: 34.78 \n Sample size: 13  Mean of sample: 21.38 SD of sample: 21.96 \n\n Null hypothesis H0 : Rahane 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Rahane 's sample average is below the 95% confidence interval of population average\n\n Rahane 's Form Status: Out-of-Form because the p value: 0.023244  is less than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("pujara.csv","Pujara")

## [1] "**************************** Form status of Pujara ****************************\n\n Population size: 145  Mean of population: 41.93 \n Sample size: 17  Mean of sample: 33.24 SD of sample: 31.74 \n\n Null hypothesis H0 : Pujara 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Pujara 's sample average is below the 95% confidence interval of population average\n\n Pujara 's Form Status: In-Form because the p value: 0.137319  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("shubman.csv","S Gill")

## [1] "**************************** Form status of S Gill ****************************\n\n Population size: 23  Mean of population: 30.43 \n Sample size: 3  Mean of sample: 51.33 SD of sample: 66.88 \n\n Null hypothesis H0 : S Gill 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : S Gill 's sample average is below the 95% confidence interval of population average\n\n S Gill 's Form Status: In-Form because the p value: 0.687033  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

3q. Predicting Runs given Balls Faced and Minutes at Crease

A multi-variate regression plane is fitted between Runs and Balls faced +Minutes at crease.

BF <- seq( 10, 400,length=15)
Mins <- seq(30,600,length=15)
newDF <- data.frame(BF,Mins)
kohli1 <- batsmanRunsPredict("kohli.csv","Kohli",newdataframe=newDF)
rohit1 <- batsmanRunsPredict("rohit.csv","Rohit",newdataframe=newDF)
pujara1 <- batsmanRunsPredict("pujara.csv","Pujara",newdataframe=newDF)
rahane1 <- batsmanRunsPredict("rahane.csv","Rahane",newdataframe=newDF)
sgill1 <- batsmanRunsPredict("shubman.csv","S Gill",newdataframe=newDF)

batsmen <-cbind(round(kohli1$Runs),round(rohit1$Runs),round(pujara1$Runs),round(rahane1$Runs),round(sgill1$Runs))
colnames(batsmen) <- c("Kohli","Rohit","Pujara","Rahane","S Gill")
newDF <- data.frame(round(newDF$BF),round(newDF$Mins))
colnames(newDF) <- c("BallsFaced","MinsAtCrease")
predictedRuns <- cbind(newDF,batsmen)
predictedRuns

##    BallsFaced MinsAtCrease Kohli Rohit Pujara Rahane S Gill
## 1          10           30     6     3      3      2      7
## 2          38           71    24    19     16     17     24
## 3          66          111    41    35     29     31     40
## 4          94          152    58    51     42     45     56
## 5         121          193    76    66     55     59     73
## 6         149          234    93    82     68     74     89
## 7         177          274   110    98     80     88    106
## 8         205          315   128   114     93    102    122
## 9         233          356   145   129    106    116    139
## 10        261          396   163   145    119    130    155
## 11        289          437   180   161    132    145    171
## 12        316          478   197   177    144    159    188
## 13        344          519   215   192    157    173    204
## 14        372          559   232   208    170    187    221
## 15        400          600   249   224    183    202    237

4. Analysis of India WTC batsmen from Jan 2016 – May 2023 against Australia

4a. Relative cumulative average

Against Australia specifically between 2016 – 2023, Pujara has the best record followed by Rahane, with Gill in hot pursuit. Kohli and Rohit trail behind

frames <- list("kohliTestAus.csv","rohitTestAus.csv","pujaraTestAus.csv","rahaneTestAus.csv","shubmanTestAus.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeBatsmanCumulativeAvgRuns(frames,names)

4b. Relative cumulative average strike rate in career

In the Strike Rate department Gill tops followed by Rohit and Rahane

frames <- list("kohliTestAus.csv","rohitTestAus.csv","pujaraTestAus.csv","rahaneTestAus.csv","shubmanTestAus.csv")
names <- list("Kohli","Rohit","Pujara","Rahane","S Gill")
relativeBatsmanCumulativeStrikeRate(frames,names)

5. Analysis of Australia WTC batsmen from Jan 2016 – May 2023

5a Basic analyses

par(mfrow=c(3,3))
par(mar=c(4,4,2,2))
batsmanRunsFreqPerf("stevesmithTest.csv","S Smith")
batsmanMeanStrikeRate("stevesmithTest.csv","S Smith")
batsmanRunsRanges("stevesmithTest.csv","S Smith")

batsmanRunsFreqPerf("warnerTest.csv","Warner")
batsmanMeanStrikeRate("warnerTest.csv","Warner")
batsmanRunsRanges("warnerTest.csv","Warner")

batsmanRunsFreqPerf("labuschagneTest.csv","M Labuschagne")
batsmanMeanStrikeRate("labuschagneTest.csv","M Labuschagne")
batsmanRunsRanges("labuschagneTest.csv","M Labuschagne")

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))
batsmanRunsFreqPerf("cgreenTest.csv","C Green")
batsmanMeanStrikeRate("cgreenTest.csv","C Green")
batsmanRunsRanges("cgreenTest.csv","C Green")

batsmanRunsFreqPerf("khwajaTest.csv","Khwaja")
batsmanMeanStrikeRate("khwajaTest.csv","Khwaja")
batsmanRunsRanges("khwajaTest.csv","Khwaja")

5b. More analyses

par(mfrow=c(3,3))
par(mar=c(4,4,2,2))
batsman4s("stevesmithTest.csv","S Smith")
batsman6s("stevesmithTest.csv","S Smith")
batsmanMeanStrikeRate("stevesmithTest.csv","S Smith")

batsman4s("warnerTest.csv","Warner")
batsman6s("warnerTest.csv","Warner")
batsmanMeanStrikeRate("warnerTest.csv","Warner")

batsman4s("labuschagneTest.csv","M Labuschagne")
batsman6s("labuschagneTest.csv","M Labuschagne")
batsmanMeanStrikeRate("labuschagneTest.csv","M Labuschagne")

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))
batsman4s("cgreenTest.csv","C Green")
batsman6s("cgreenTest.csv","C Green")
batsmanMeanStrikeRate("cgreenTest.csv","C Green")

batsman4s("khwajaTest.csv","Khwaja")
batsman6s("khwajaTest.csv","Khwaja")
batsmanMeanStrikeRate("khwajaTest.csv","Khwaja")

5c.Boxplot histogram plot

This plot shows a combined boxplot of the Runs ranges and a histog2ram of the Runs Frequency

Smith, Labuschagne has an average of 53+ since 2016!! Warner & Khwaja are at ~46

batsmanPerfBoxHist("stevesmithTest.csv","S Smith")

batsmanPerfBoxHist("warnerTest.csv","Warner")

batsmanPerfBoxHist("labuschagneTest.csv","M Labuschagne")

batsmanPerfBoxHist("cgreenTest.csv","C Green")

batsmanPerfBoxHist("khwajaTest.csv","Khwaja")

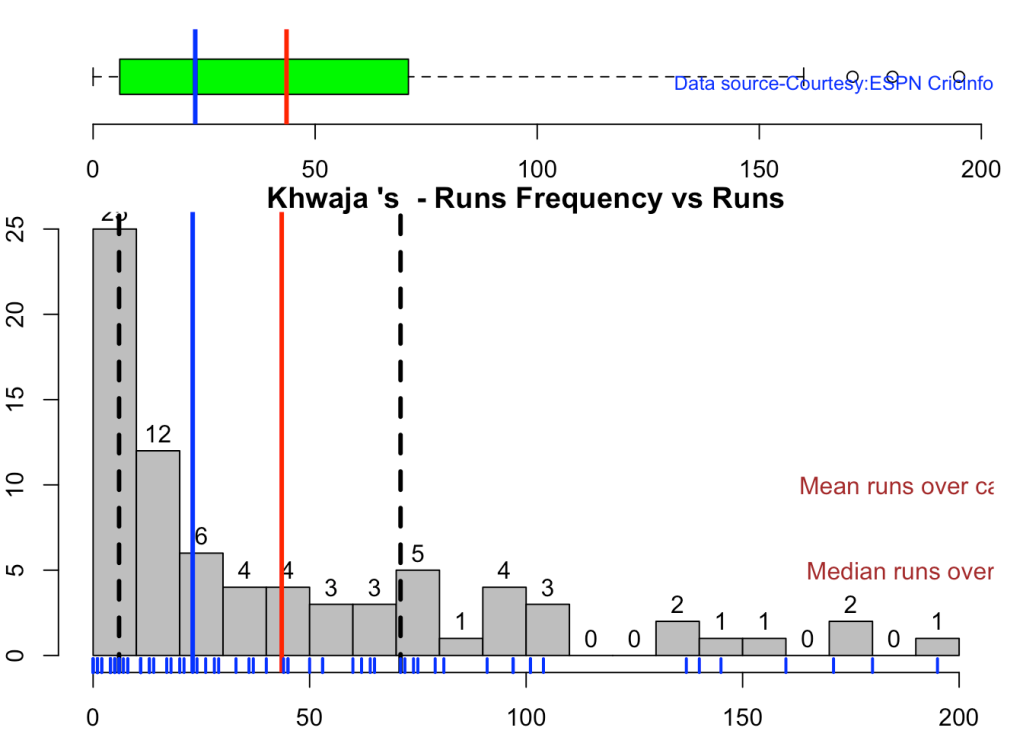
5d. Contribution to won and lost matches

For the 2 functions below you will have to use the getPlayerDataSp() function. Australia has won matches when Smith, Warner and Khwaja have played well.

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))
batsmanContributionWonLost("stevesmithsp.csv","S Smith")
batsmanContributionWonLost("warnersp.csv","Warner")
batsmanContributionWonLost("labuschagnesp.csv","M Labuschagne")
batsmanContributionWonLost("cgreensp.csv","C Green")

batsmanContributionWonLost("khwajasp.csv","Khwaja")

5e. Performance at home and overseas

This function also requires the use of getPlayerDataSp() as shown above. This can only be used for Test matches

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanPerfHomeAway("stevesmithsp.csv","S Smith")
batsmanPerfHomeAway("warnersp.csv","Warner")
batsmanPerfHomeAway("labuschagnesp.csv","M Labuschagne")
batsmanPerfHomeAway("cgreensp.csv","C Green")

batsmanPerfHomeAway("khwajasp.csv","Khwaja")

5f. Batsman average at different venues

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanAvgRunsGround("stevesmithTest.csv","S Smith")
batsmanAvgRunsGround("warnerTest.csv","Warner")
batsmanAvgRunsGround("labuschagneTest.csv","M Labuschagne")
batsmanAvgRunsGround("cgreenTest.csv","C Green")

batsmanAvgRunsGround("khwajaTest.csv","Khwaja")

5g. Batsman average against different opposition

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanAvgRunsOpposition("stevesmithTest.csv","S Smith")
batsmanAvgRunsOpposition("warnerTest.csv","Warner")
batsmanAvgRunsOpposition("labuschagneTest.csv","M Labuschagne")
batsmanAvgRunsOpposition("khwajaTest.csv","Khwaja")

5h. Runs Likelihood of batsman

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanRunsLikelihood("stevesmithTest.csv","S Smith")

## Summary of  S Smith 's runs scoring likelihood
## **************************************************
## 
## There is a 58.76 % likelihood that S Smith  will make  21 Runs in  38 balls over 56  Minutes 
## There is a 24.74 % likelihood that S Smith  will make  70 Runs in  148 balls over  210  Minutes 
## There is a 16.49 % likelihood that S Smith  will make  148 Runs in  268 balls over 398  Minutes

batsmanRunsLikelihood("warnerTest.csv","Warner")

## Summary of  Warner 's runs scoring likelihood
## **************************************************
## 
## There is a 7.22 % likelihood that Warner  will make  155 Runs in  253 balls over 372  Minutes 
## There is a 62.89 % likelihood that Warner  will make  14 Runs in  21 balls over  32  Minutes 
## There is a 29.9 % likelihood that Warner  will make  65 Runs in  94 balls over 135  Minutes

batsmanRunsLikelihood("labuschagneTest.csv","M Labuschagne")

## Summary of  M Labuschagne 's runs scoring likelihood
## **************************************************
## 
## There is a 32.76 % likelihood that M Labuschagne  will make  74 Runs in  144 balls over 206  Minutes 
## There is a 55.17 % likelihood that M Labuschagne  will make  22 Runs in  37 balls over  54  Minutes 
## There is a 12.07 % likelihood that M Labuschagne  will make  168 Runs in  297 balls over 420  Minutes

batsmanRunsLikelihood("khwajaTest.csv","Khwaja")

## Summary of  Khwaja 's runs scoring likelihood
## **************************************************
## 
## There is a 64.94 % likelihood that Khwaja  will make  14 Runs in  29 balls over 42  Minutes 
## There is a 27.27 % likelihood that Khwaja  will make  79 Runs in  148 balls over  210  Minutes 
## There is a 7.79 % likelihood that Khwaja  will make  165 Runs in  351 balls over 515  Minutes

5i. Moving average of batsman

Smith and Warner’s moving average has been on a downward trend lately. Khwaja is playing well

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanMovingAverage("stevesmith.csv","S Smith")
batsmanMovingAverage("warner.csv","Warner")
batsmanMovingAverage("labuschagne.csv","M Labuschagne")
batsmanMovingAverage("khwaja.csv","Khwaja")

5j. Cumulative Average runs of batsman in career

Labuschagne, SMith and Warner havwe very good cumulative average

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanCumulativeAverageRuns("stevesmithTest.csv","S Smith")

batsmanCumulativeAverageRuns("warnerTest.csv","Warner")

batsmanCumulativeAverageRuns("labuschagneTest.csv","M Labuschagne")

batsmanCumulativeAverageRuns("khwajaTest.csv","Khwaja")

5k. Cumulative Average strike rate of batsman in career

Warner towers over the others in the cumulative strike rate, followed by Labuschagne and Smith

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanCumulativeStrikeRate("stevesmithTest.csv","S Smith")

batsmanCumulativeStrikeRate("warnerTest.csv","Warner")

batsmanCumulativeStrikeRate("labuschagneTest.csv","M Labuschagne")

batsmanCumulativeStrikeRate("khwajaTest.csv","Khwaja")

5l. Future Runs forecast

Here are plots that forecast how the batsman will perform in future. In this case 90% of the career runs trend is uses as the training set. the remaining 10% is the test set.

Take a look at the runs forecasted for the batsman below.

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

batsmanPerfForecast("stevesmithTest.csv","S Smith")
batsmanPerfForecast("warnerTest.csv","Warner")
batsmanPerfForecast("labuschagneTest.csv","M Labuschagne")
batsmanPerfForecast("khwajaTest.csv","Khwaja")

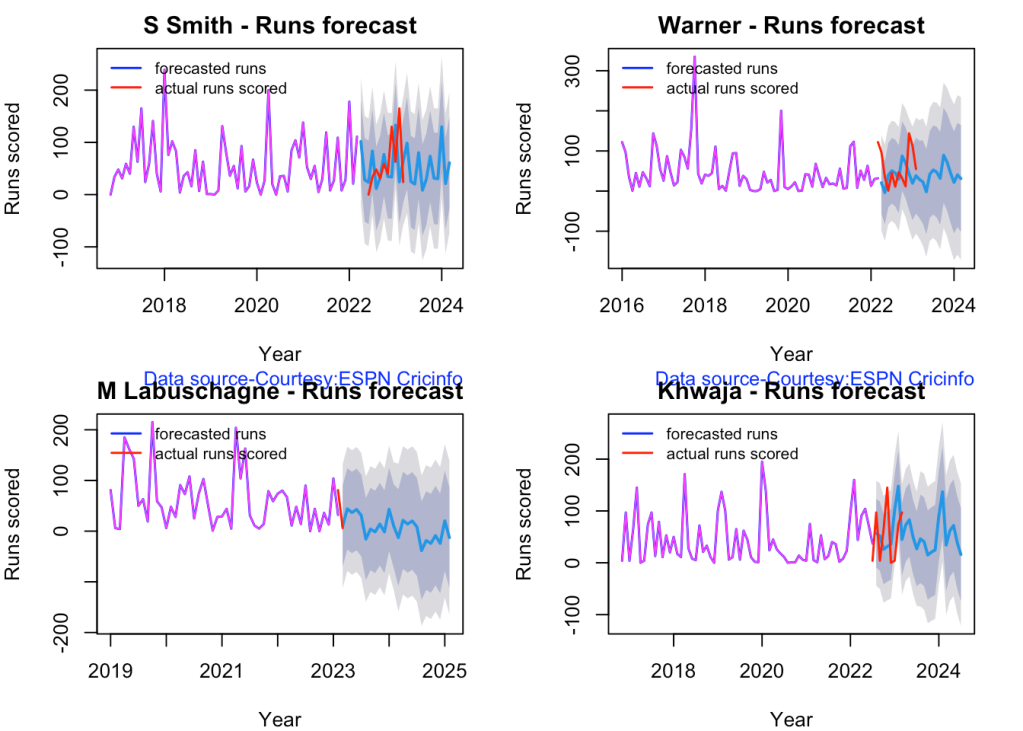
5m. Relative Mean Strike Rate plot

The plot below compares the Mean Strike Rate of the batsman for each of the runs ranges of 10 and plots them. The plot indicate the following

frames <- list("stevesmithTest.csv","warnerTest.csv","khwajaTest.csv","labuschagneTest.csv","cgreenTest.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeBatsmanSR(frames,names)

5n. Relative Runs Frequency plot

The plot below gives the relative Runs Frequency Percetages for each 10 run bucket. The plot below show

frames <- list("stevesmithTest.csv","warnerTest.csv","khwajaTest.csv","labuschagneTest.csv","cgreenTest.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeRunsFreqPerf(frames,names)

5o. Relative cumulative average runs in career

frames <- list("stevesmithTest.csv","warnerTest.csv","khwajaTest.csv","labuschagneTest.csv","cgreenTest.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeBatsmanCumulativeAvgRuns(frames,names)

5p. Relative cumulative average strike rate in career

frames <- list("stevesmithTest.csv","warnerTest.csv","khwajaTest.csv","labuschagneTest.csv","cgreenTest.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeBatsmanCumulativeStrikeRate(frames,names)

5q. Check Batsman In-Form or Out-of-Form

A significance value of 0.05 is chosen and p-value us computed If p-value >= .05 – Batsman In-Form If p-value < 0.05 – Batsman Out-of-Form

This is done for the Top 4 batsman

checkBatsmanInForm("stevesmith.csv","S Smith")

## [1] "**************************** Form status of S Smith ****************************\n\n Population size: 144  Mean of population: 53.76 \n Sample size: 17  Mean of sample: 45.65 SD of sample: 56.4 \n\n Null hypothesis H0 : S Smith 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : S Smith 's sample average is below the 95% confidence interval of population average\n\n S Smith 's Form Status: In-Form because the p value: 0.280533  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("warner.csv","Warner")

## [1] "**************************** Form status of Warner ****************************\n\n Population size: 164  Mean of population: 45.2 \n Sample size: 19  Mean of sample: 26.63 SD of sample: 44.62 \n\n Null hypothesis H0 : Warner 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Warner 's sample average is below the 95% confidence interval of population average\n\n Warner 's Form Status: Out-of-Form because the p value: 0.042744  is less than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("labuschagne.csv","M Labuschagne")

## [1] "**************************** Form status of M Labuschagne ****************************\n\n Population size: 52  Mean of population: 59.56 \n Sample size: 6  Mean of sample: 29.67 SD of sample: 19.96 \n\n Null hypothesis H0 : M Labuschagne 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : M Labuschagne 's sample average is below the 95% confidence interval of population average\n\n M Labuschagne 's Form Status: Out-of-Form because the p value: 0.005239  is less than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBatsmanInForm("khwaja.csv","Khwaja")

## [1] "**************************** Form status of Khwaja ****************************\n\n Population size: 89  Mean of population: 41.62 \n Sample size: 10  Mean of sample: 53.1 SD of sample: 76.34 \n\n Null hypothesis H0 : Khwaja 's sample average is within 95% confidence interval of population average\n Alternative hypothesis Ha : Khwaja 's sample average is below the 95% confidence interval of population average\n\n Khwaja 's Form Status: In-Form because the p value: 0.677691  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

5r. Predicting Runs given Balls Faced and Minutes at Crease

A multi-variate regression plane is fitted between Runs and Balls faced +Minutes at crease.

BF <- seq( 10, 400,length=15)
Mins <- seq(30,600,length=15)
newDF <- data.frame(BF,Mins)
ssmith1 <- batsmanRunsPredict("stevesmith.csv","S Smith",newdataframe=newDF)

warner1 <- batsmanRunsPredict("warner.csv","Warner",newdataframe=newDF)

khwaja1 <- batsmanRunsPredict("khwaja.csv","Khwaja",newdataframe=newDF)
labuschagne1 <- batsmanRunsPredict("labuschagne.csv","Labuschagne",newdataframe=newDF)

cgreen1 <- batsmanRunsPredict("cgreen.csv","C Green",newdataframe=newDF)

batsmen <-cbind(round(ssmith1$Runs),round(warner1$Runs),round(khwaja1$Runs),round(labuschagne1$Runs),round(cgreen1$Runs))
colnames(batsmen) <- c("S Smith","Warner","Khwaja","Labuschagne","C Green")
newDF <- data.frame(round(newDF$BF),round(newDF$Mins))
colnames(newDF) <- c("BallsFaced","MinsAtCrease")
predictedRuns <- cbind(newDF,batsmen)
predictedRuns

##    BallsFaced MinsAtCrease S Smith Warner Khwaja Labuschagne C Green
## 1          10           30       7     10     10           9      13
## 2          38           71      23     30     24          24      29
## 3          66          111      38     50     38          40      44
## 4          94          152      53     70     53          55      60
## 5         121          193      69     90     67          70      75
## 6         149          234      84    110     81          85      91
## 7         177          274     100    130     95         100     106
## 8         205          315     115    150    109         116     122
## 9         233          356     130    170    123         131     137
## 10        261          396     146    190    137         146     153
## 11        289          437     161    210    151         161     168
## 12        316          478     177    230    165         176     184
## 13        344          519     192    250    179         192     199
## 14        372          559     207    270    193         207     215
## 15        400          600     223    290    207         222     230

6. Analysis of Australia WTC batsmen from Jan 2016 – May 2023 against India

6a. Relative cumulative average runs in career

Labuschagne, Smith and C Green have good records against India

frames <- list("stevesmithTestInd.csv","warnerTestInd.csv","khwajaTestInd.csv","labuschagneTestInd.csv","cgreenTestInd.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeBatsmanCumulativeAvgRuns(frames,names)

6b. Relative cumulative average strike rate in career

Warner, Labuschagne and Smith have a good strike rate against India

frames <- list("stevesmithTestInd.csv","warnerTestInd.csv","khwajaTestInd.csv","labuschagneTestInd.csv","cgreenTestInd.csv")
names <- list("S Smith","Warner","Khwaja","Labuschagne","C Green")
relativeBatsmanCumulativeStrikeRate(frames,names)

7. Analysis of India WTC bowlers from Jan 2016 – May 2023

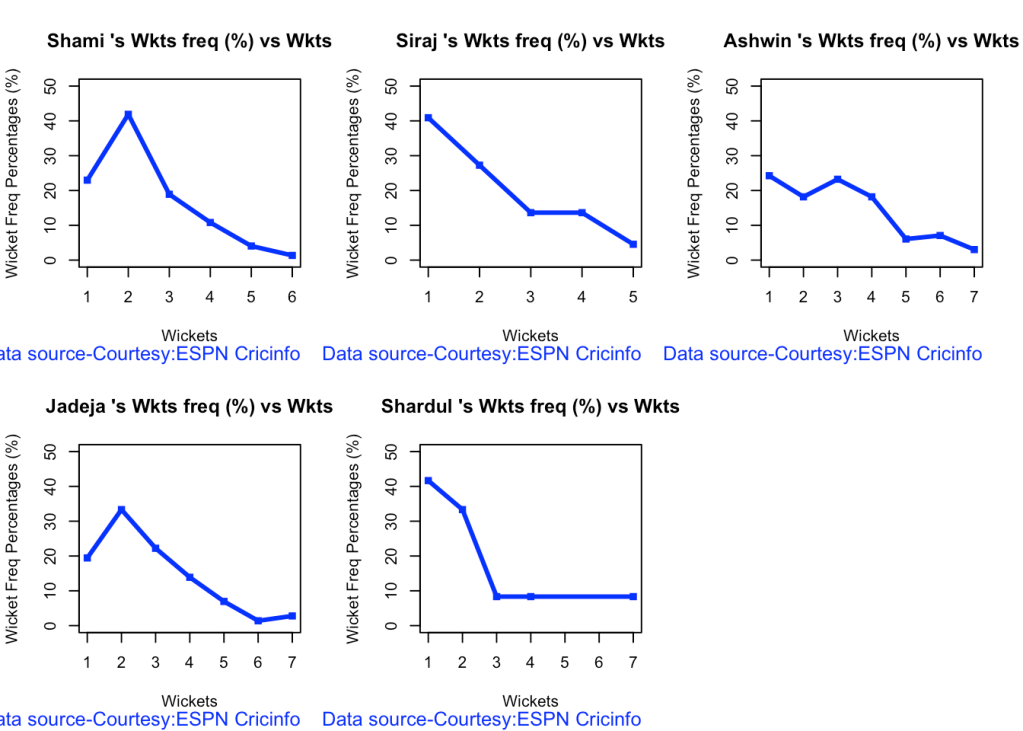
7a Wickets frequency chart

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))
bowlerWktsFreqPercent("shamiTest.csv","Shami")
bowlerWktsFreqPercent("sirajTest.csv","Siraj")
bowlerWktsFreqPercent("ashwinTest.csv","Ashwin")
bowlerWktsFreqPercent("jadejaTest.csv","Jadeja")
bowlerWktsFreqPercent("shardulTest.csv","Shardul")

7b Wickets Runs chart

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerWktsRunsPlot("shamiTest.csv","Shami")
bowlerWktsRunsPlot("sirajTest.csv","Siraj")
bowlerWktsRunsPlot("ashwinTest.csv","Ashwin")
bowlerWktsRunsPlot("jadejaTest.csv","Jadeja")
bowlerWktsRunsPlot("shardulTest.csv","Shardul")

7c. Average wickets at different venues

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerAvgWktsGround("shamiTest.csv","Shami")
bowlerAvgWktsGround("sirajTest.csv","Siraj")
bowlerAvgWktsGround("ashwinTest.csv","Ashwin")
bowlerAvgWktsGround("jadejaTest.csv","Jadeja")
bowlerAvgWktsGround("shardulTest.csv","Shardul")

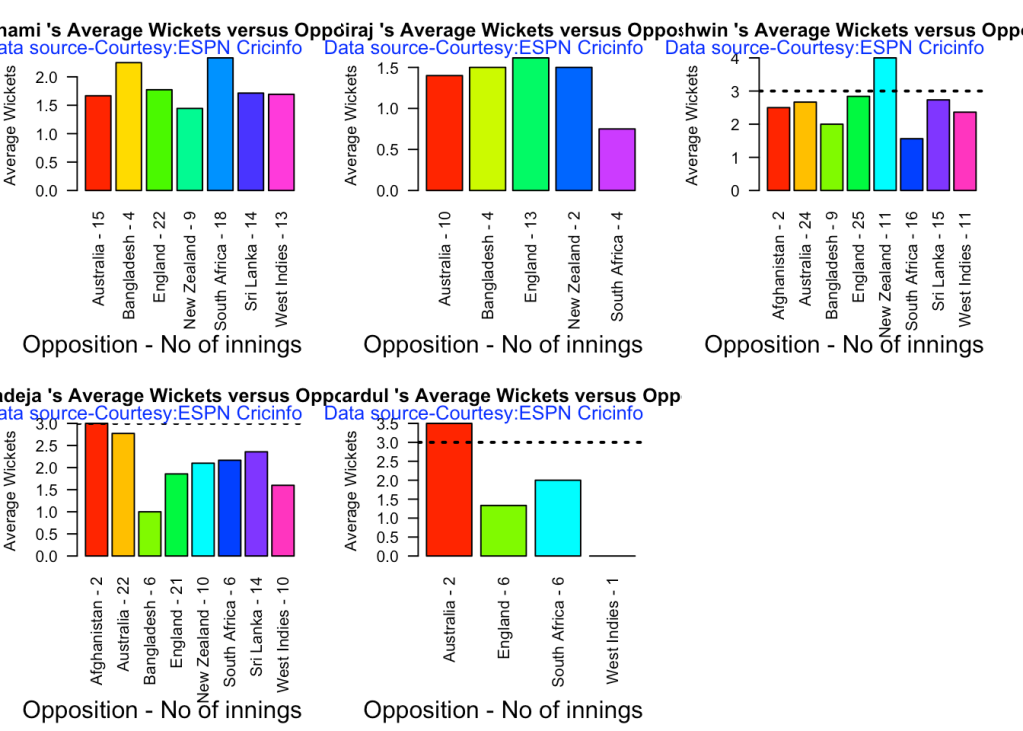
7d Average wickets against different opposition

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerAvgWktsOpposition("shamiTest.csv","Shami")
bowlerAvgWktsOpposition("sirajTest.csv","Siraj")
bowlerAvgWktsOpposition("ashwinTest.csv","Ashwin")
bowlerAvgWktsOpposition("jadejaTest.csv","Jadeja")
bowlerAvgWktsOpposition("shardulTest.csv","Shardul")

7e Cumulative average wickets taken

Ashwin’s performance has dropped over the years, while Siraj has been becoming better

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

bowlerCumulativeAvgWickets("shamiTest.csv","Shami")

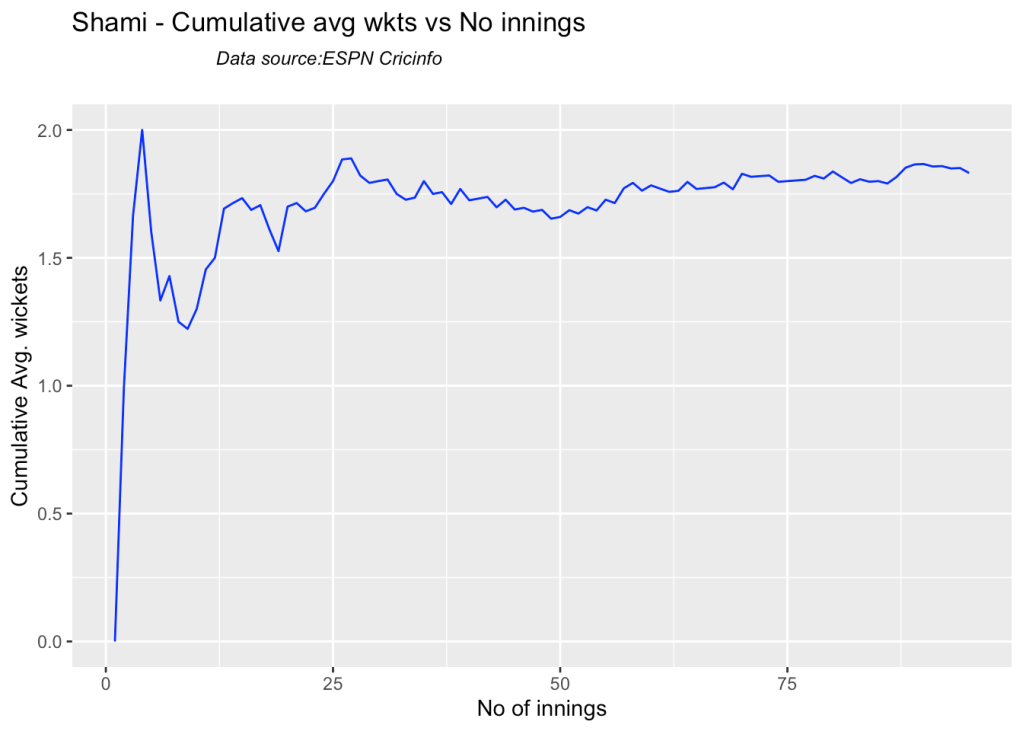
bowlerCumulativeAvgWickets("sirajTest.csv","Siraj")

bowlerCumulativeAvgWickets("ashwinTest.csv","Ashwin")

bowlerCumulativeAvgWickets("jadejaTest.csv","Jadeja")

bowlerCumulativeAvgWickets("shardulTest.csv","Shardul")

7g Cumulative average economy rate

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerCumulativeAvgEconRate("shamiTest.csv","Shami")

bowlerCumulativeAvgEconRate("sirajTest.csv","Siraj")

bowlerCumulativeAvgEconRate("ashwinTest.csv","Ashwin")

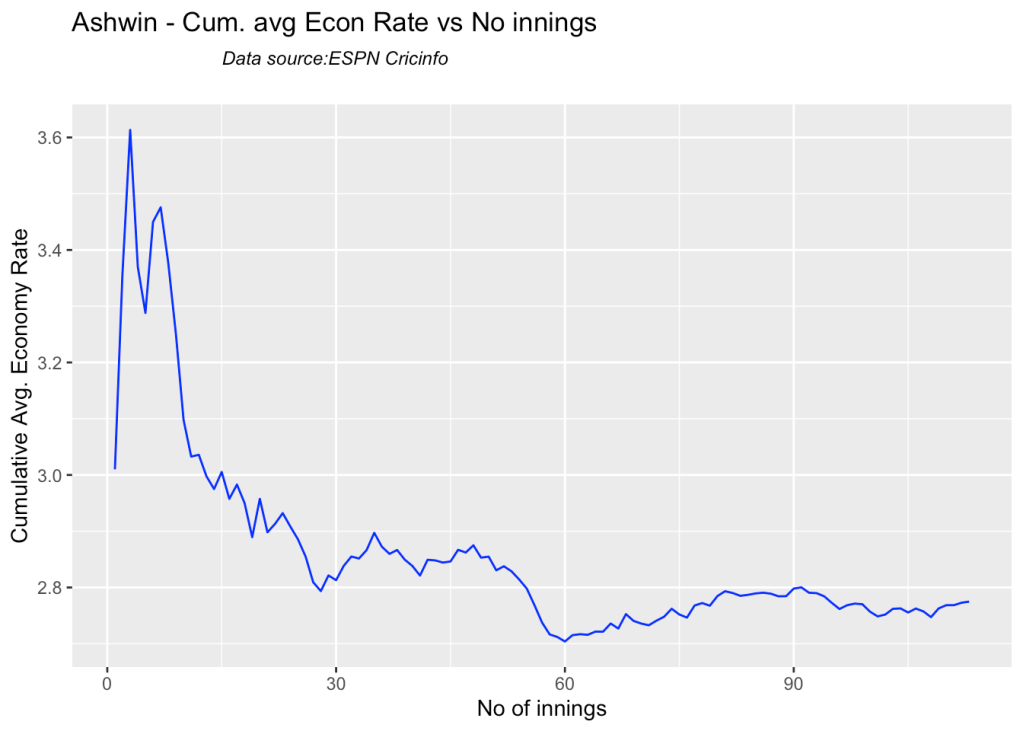
bowlerCumulativeAvgEconRate("jadejaTest.csv","Jadeja")

bowlerCumulativeAvgEconRate("shardulTest.csv","Shardul")

7h Wicket forecast

Here are plots that forecast how the bowler will perform in future. In this case 90% of the career wickets trend is used as the training set. the remaining 10% is the test set.

A Holt-Winters forecasting model is used to forecast future performance based on the 90% training set. The forecasted wickets trend is plotted. The test set is also plotted to see how close the forecast and the actual matches

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerPerfForecast("shamiTest.csv","Shami")
#bowlerPerfForecast("sirajTest.csv","Siraj")
bowlerPerfForecast("ashwinTest.csv","Ashwin")
bowlerPerfForecast("jadejaTest.csv","Jadeja")
bowlerPerfForecast("shardulTest.csv","Shardul")

7i Relative Wickets Frequency Percentage

frames <- list("shamiTest.csv","sirajTest.csv","ashwinTest.csv","jadejaTest.csv","shardulTest.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlingPerf(frames,names)

7j Relative Economy Rate against wickets taken

frames <- list("shamiTest.csv","sirajTest.csv","ashwinTest.csv","jadejaTest.csv","shardulTest.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlingER(frames,names)

7k Relative cumulative average wickets of bowlers in career

Ashwin has the highest wickets followed by Jadeja against all teams

frames <- list("shamiTest.csv","sirajTest.csv","ashwinTest.csv","jadejaTest.csv","shardulTest.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlerCumulativeAvgWickets(frames,names)

7l Relative cumulative average economy rate of bowlers

Jadeja has the best economy rate followed by Ashwin

frames <- list("shamiTest.csv","sirajTest.csv","ashwinTest.csv","jadejaTest.csv","shardulTest.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlerCumulativeAvgEconRate(frames,names)

7m Check for bowler in-form/out-of-form

The below computation uses Null Hypothesis testing and p-value to determine if the bowler is in-form or out-of-form. For this 90% of the career wickets is chosen as the population and the mean computed. The last 10% is chosen to be the sample set and the sample Mean and the sample Standard Deviation are caculated.

The Null Hypothesis (H0) assumes that the bowler continues to stay in-form where the sample mean is within 95% confidence interval of population mean The Alternative (Ha) assumes that the bowler is out of form the sample mean is beyond the 95% confidence interval of the population mean.

A significance value of 0.05 is chosen and p-value us computed If p-value >= .05 – Batsman In-Form If p-value < 0.05 – Batsman Out-of-Form

Note: The check for the form status of the bowlers indicate

checkBowlerInForm("shami.csv","Shami")

## [1] "**************************** Form status of Shami ****************************\n\n Population size: 106  Mean of population: 1.93 \n Sample size: 12  Mean of sample: 1.33 SD of sample: 1.23 \n\n Null hypothesis H0 : Shami 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Shami 's sample average is below the 95% confidence\n        interval of population average\n\n Shami 's Form Status: In-Form because the p value: 0.058427  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("siraj.csv","Siraj")

## [1] "**************************** Form status of Siraj ****************************\n\n Population size: 29  Mean of population: 1.59 \n Sample size: 4  Mean of sample: 0.25 SD of sample: 0.5 \n\n Null hypothesis H0 : Siraj 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Siraj 's sample average is below the 95% confidence\n        interval of population average\n\n Siraj 's Form Status: Out-of-Form because the p value: 0.002923  is less than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("ashwin.csv","Ashwin")

## [1] "**************************** Form status of Ashwin ****************************\n\n Population size: 154  Mean of population: 2.77 \n Sample size: 18  Mean of sample: 2.44 SD of sample: 1.76 \n\n Null hypothesis H0 : Ashwin 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Ashwin 's sample average is below the 95% confidence\n        interval of population average\n\n Ashwin 's Form Status: In-Form because the p value: 0.218345  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("jadeja.csv","Jadeja")

## [1] "**************************** Form status of Jadeja ****************************\n\n Population size: 108  Mean of population: 2.22 \n Sample size: 12  Mean of sample: 1.92 SD of sample: 2.35 \n\n Null hypothesis H0 : Jadeja 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Jadeja 's sample average is below the 95% confidence\n        interval of population average\n\n Jadeja 's Form Status: In-Form because the p value: 0.333095  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("shardul.csv","Shardul")

## [1] "**************************** Form status of Shardul ****************************\n\n Population size: 13  Mean of population: 2 \n Sample size: 2  Mean of sample: 0.5 SD of sample: 0.71 \n\n Null hypothesis H0 : Shardul 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Shardul 's sample average is below the 95% confidence\n        interval of population average\n\n Shardul 's Form Status: Out-of-Form because the p value: 0.04807  is less than alpha=  0.05 \n *******************************************************************************************\n\n"

8. Analysis of India WTC bowlers from Jan 2016 – May 2023 against Australia

8a Relative cumulative average wickets of bowlers in career

Against Australia specifically Jadeja has the best record followed by Ashwin

frames <- list("shamiTestAus.csv","sirajTestAus.csv","ashwinTestAus.csv","jadejaTestAus.csv","shardulTestAus.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlerCumulativeAvgWickets(frames,names)

8b Relative cumulative average economy rate of bowlers

Jadeja has the best economy followed by Siraj, then Ashwin

frames <- list("shamiTestAus.csv","sirajTestAus.csv","ashwinTestAus.csv","jadejaTestAus.csv","shardulTestAus.csv")
names <- list("Shami","Siraj","Ashwin","Jadeja","Shardul")
relativeBowlerCumulativeAvgEconRate(frames,names)

8. Analysis of India WTC bowlers from Jan 2016 – May 2023

8a. Wickets frequency chart

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))
bowlerWktsFreqPercent("cumminsTest.csv","Cummins")
bowlerWktsFreqPercent("starcTest.csv","Starc")
bowlerWktsFreqPercent("hazzlewoodTest.csv","Hazzlewood")
bowlerWktsFreqPercent("todd.csv","Todd")
bowlerWktsFreqPercent("lyonTest.csv","N Lyon")

8b. Wickets frequency chart

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerWktsRunsPlot("cumminsTest.csv","Cummins")
bowlerWktsRunsPlot("starcTest.csv","Starc")
bowlerWktsRunsPlot("hazzlewoodTest.csv","Hazzlewood")
bowlerWktsRunsPlot("todd.csv","Todd")
bowlerWktsRunsPlot("lyonTest.csv","N Lyon")

8c. Average wickets at different venues

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerAvgWktsGround("cumminsTest.csv","Cummins")
bowlerAvgWktsGround("starcTest.csv","Starc")
bowlerAvgWktsGround("hazzlewoodTest.csv","Hazzlewood")
bowlerAvgWktsGround("todd.csv","Todd")
bowlerAvgWktsGround("lyonTest.csv","N Lyon")

8d Average wickets against different opposition

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerAvgWktsOpposition("cumminsTest.csv","Cummins")
bowlerAvgWktsOpposition("starcTest.csv","Starc")
bowlerAvgWktsOpposition("hazzlewoodTest.csv","Hazzlewood")
bowlerAvgWktsOpposition("todd.csv","Todd")
bowlerAvgWktsOpposition("lyonTest.csv","N Lyon")

8e Cumulative average wickets taken

par(mfrow=c(2,2))
par(mar=c(4,4,2,2))

bowlerCumulativeAvgWickets("cumminsTest.csv","Cummins")

bowlerCumulativeAvgWickets("starcTest.csv","Starc")

bowlerCumulativeAvgWickets("hazzlewoodTest.csv","Hazzlewood")

bowlerCumulativeAvgWickets("todd.csv","Todd")

bowlerCumulativeAvgWickets("lyonTest.csv","N Lyon")

8g Cumulative average economy rate

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerCumulativeAvgEconRate("cumminsTest.csv","Cummins")

bowlerCumulativeAvgEconRate("starcTest.csv","Starc")

bowlerCumulativeAvgEconRate("hazzlewoodTest.csv","Hazzlewood")

bowlerCumulativeAvgEconRate("todd.csv","Todd")

bowlerCumulativeAvgEconRate("lyonTest.csv","N Lyon")

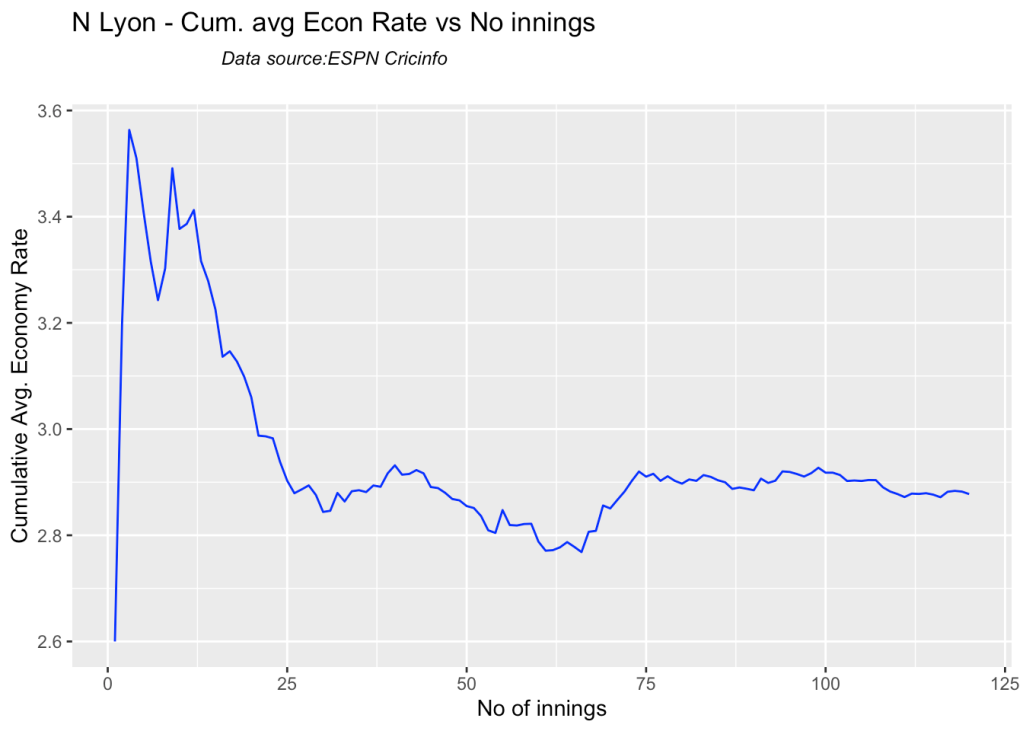
8f. Future Wickets forecast

Here are plots that forecast how the bowler will perform in future. In this case 90% of the career wickets trend is used as the training set. the remaining 10% is the test set.

A Holt-Winters forecasting model is used to forecast future performance based on the 90% training set. The forecated wickets trend is plotted. The test set is also plotted to see how close the forecast and the actual matches

par(mfrow=c(2,3))
par(mar=c(4,4,2,2))

bowlerPerfForecast("cumminsTest.csv","Cummins")
bowlerPerfForecast("starcTest.csv","Starc")
bowlerPerfForecast("hazzlewoodTest.csv","Hazzlewood")
bowlerPerfForecast("lyonTest.csv","N Lyon")

8i. Relative Wickets Frequency Percentage

frames <- list("cumminsTest.csv","starcTest.csv","hazzlewoodTest.csv","todd.csv","lyonTest.csv")
names <- list("Cummins","Starc","Hazzlewood","Todd","N Lyon")
relativeBowlingPerf(frames,names)

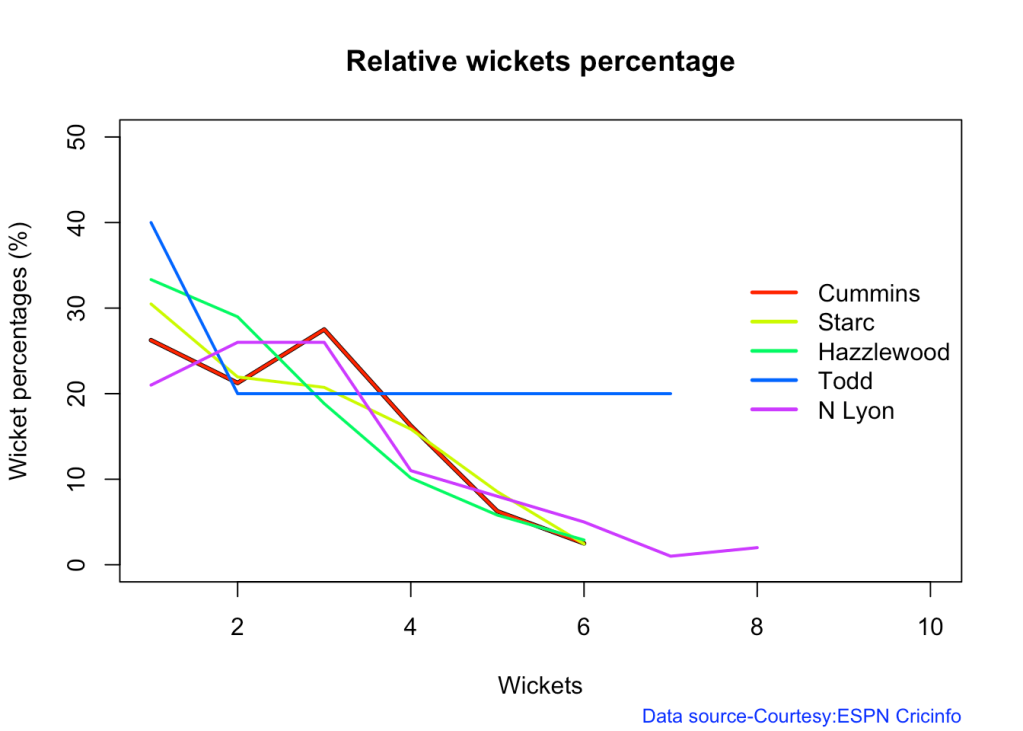
8j Relative Economy Rate against wickets taken

frames <- list("cumminsTest.csv","starcTest.csv","hazzlewoodTest.csv","todd.csv","lyonTest.csv")
names <- list("Cummins","Starc","Hazzlewood","Todd","N Lyon")
relativeBowlingER(frames,names)

8k Relative cumulative average wickets of bowlers in career

Cummins, Starc and Lyons are the best performers

frames <- list("cumminsTest.csv","starcTest.csv","hazzlewoodTest.csv","todd.csv","lyonTest.csv")
names <- list("Cummins","Starc","Hazzlewood","Todd","N Lyon")
relativeBowlerCumulativeAvgWickets(frames,names)

8l Relative cumulative average economy rate of bowlers

Hazzlewood, Cummins have the best economy against all oppostion

frames <- list("cumminsTest.csv","starcTest.csv","hazzlewoodTest.csv","todd.csv","lyonTest.csv")
names <- list("Cummins","Starc","Hazzlewood","Todd","N Lyon")
relativeBowlerCumulativeAvgEconRate(frames,names)

8o Check for bowler in-form/out-of-form

A significance value of 0.05 is chosen and p-value us computed If p-value >= .05 – Batsman In-Form If p-value < 0.05 – Batsman Out-of-Form

Note: The check for the form status of the bowlers indicate

checkBowlerInForm("cummins.csv","Cummins")

## [1] "**************************** Form status of Cummins ****************************\n\n Population size: 81  Mean of population: 2.46 \n Sample size: 9  Mean of sample: 2 SD of sample: 1.5 \n\n Null hypothesis H0 : Cummins 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Cummins 's sample average is below the 95% confidence\n        interval of population average\n\n Cummins 's Form Status: In-Form because the p value: 0.190785  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("starc.csv","Starc")

## [1] "**************************** Form status of Starc ****************************\n\n Population size: 126  Mean of population: 2.18 \n Sample size: 15  Mean of sample: 1.67 SD of sample: 1.18 \n\n Null hypothesis H0 : Starc 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Starc 's sample average is below the 95% confidence\n        interval of population average\n\n Starc 's Form Status: In-Form because the p value: 0.057433  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("hazzlewood.csv","Hazzlewood")

## [1] "**************************** Form status of Hazzlewood ****************************\n\n Population size: 99  Mean of population: 2.04 \n Sample size: 12  Mean of sample: 1.67 SD of sample: 1.5 \n\n Null hypothesis H0 : Hazzlewood 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : Hazzlewood 's sample average is below the 95% confidence\n        interval of population average\n\n Hazzlewood 's Form Status: In-Form because the p value: 0.204787  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

checkBowlerInForm("lyon.csv","N Lyon")

## [1] "**************************** Form status of N Lyon ****************************\n\n Population size: 193  Mean of population: 2.08 \n Sample size: 22  Mean of sample: 2.95 SD of sample: 1.96 \n\n Null hypothesis H0 : N Lyon 's sample average is within 95% confidence interval \n        of population average\n Alternative hypothesis Ha : N Lyon 's sample average is below the 95% confidence\n        interval of population average\n\n N Lyon 's Form Status: In-Form because the p value: 0.975407  is greater than alpha=  0.05 \n *******************************************************************************************\n\n"

9. Analysis of Australia WTC bowlers from Jan 2016 – May 2023 against India

9a Relative cumulative average wickets of bowlers in career

Against India Lyon, Cummins and Hazzlewood have performed well

frames <- list("cumminsTestInd.csv","starcTestInd.csv","hazzlewoodTestInd.csv","lyonTestInd.csv")
names <- list("Cummins","Starc","Hazzlewood","N Lyon")
relativeBowlerCumulativeAvgWickets(frames,names)

9b Relative cumulative average economy rate of bowlers

Hazzlewood, Lyon have a good economy rate against India

frames <- list("cumminsTestInd.csv","starcTestInd.csv","hazzlewoodTestInd.csv","lyonTestInd.csv")
names <- list("Cummins","Starc","Hazzlewood","N Lyon")
relativeBowlerCumulativeAvgEconRate(frames,names)

10 Analysis of teams – India, Australia

#The data for India & Australia teams were obtained with the following calls

#indiaTest <-getTeamDataHomeAway(dir=".",teamView="bat",matchType="Test",file="indiaTest.csv",save=TRUE,teamName="India")
#australiaTest <- getTeamDataHomeAway(matchType="Test",file="australiaTest.csv",save=TRUE,teamName="Australia")

10a. Win-loss of India against all oppositions in Test cricket

Against Australia India has won 17 times, lost 60 and drawn 22 in Australia. At home India won 42, tied 2, lost 28 and drawn 24

teamWinLossStatusVsOpposition("indiaTest.csv",teamName="India",opposition=c("all"),homeOrAway=c("all"),matchType="Test",plot=TRUE)

10b. Win-loss of Australia against all oppositions in Test cricket

teamWinLossStatusVsOpposition("australiaTest.csv",teamName="Australia",opposition=c("all"),homeOrAway=c("all"),matchType="Test",plot=TRUE)

10c. Win-loss of India against Australia in Test cricket

Against Australia India has won 17 times, lost 60 and drawn 22 in Australia. At home India won 42, tied 2, lost 28 and drawn 24

teamWinLossStatusVsOpposition("indiaTest.csv",teamName="India",opposition=c("Australia"),homeOrAway=c("all"),matchType="Test",plot=TRUE)

10d. Win-loss of India at all away venues

At the Oval where WTC is going to be held India has won 4, lost 10 and drawn 10.

teamWinLossStatusAtGrounds("indiaTest.csv",teamName="India",opposition=c("all"),homeOrAway=c("away"),matchType="Test",plot=TRUE)

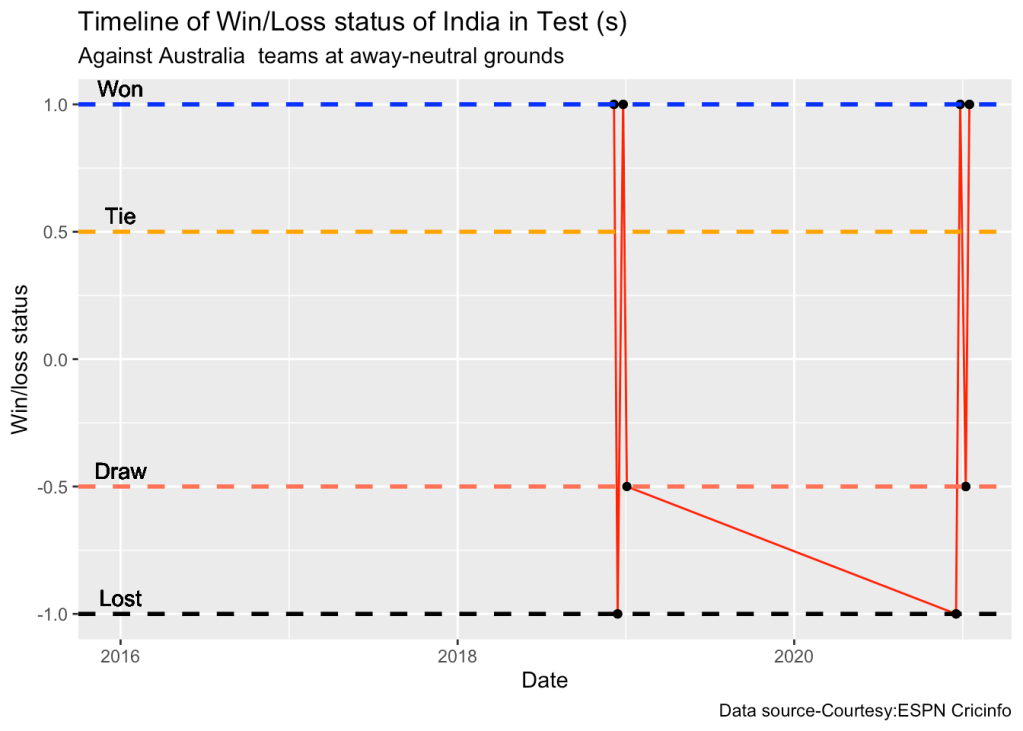
10d. Timeline of win-loss of India against Australia in Test cricket

plotTimelineofWinsLosses("indiaTest.csv",team="India",opposition=c("Australia"),
                         homeOrAway=c("away","neutral"), startDate="2016-01-01",endDate="2023-05-01")

11. Conclusion

The above analysis performs various analysis of India and Australia in home and away matches. While we know the performance of the player at India or Australia, we cannot judge how the match will progress in the neutral, swinging conditions of the Oval. Let us hope for a good match!

Feel free to try out your own analysis with cricketr. Have fun with cricketr!!

Also see

To see all posts click Index of posts

IPL 2023:GooglyPlusPlus now with by AI/ML models, near real-time analytics!

It is carnival time again as IPL 2023 is underway!! The new GooglyPlusPlus now includes AI/ML models for computing ball-by-ball Win Probability of matches and each individual player’s Win Probability Contribution (WPC). GooglyPlusPlus uses 2 ML models

Deep Learning (Tensorflow) – accuracy : 0.8584
Logistic Regression (glmnet-tidymodels) : 0.728

Besides, as before, GooglyPlusPlus will also include the usual near real-time analytics with the Shiny app being automatically updated with the previous day’s match data.

Note: The Win Probability Computation can also be done on a live feed of streaming data. Since, I don’t have access to live feeds, the app will show how Win Probability changed during the course of completed matches. For more details on Win Probability and Win Probability Contribution see my posts

GooglyPlusPlus has been also updated with all the latest T20 league’s match data. It includes data from BBL 2022, NTB 2022, CPL 2022, PSL 2023, ICC T20 2022 and now IPL 2023.

GooglyPlusPlus has the following functionality

Batsman tab: For detailed analysis of batsmen
Bowler tab: For detailed analysis of bowlers
Match tab: Analysis of individual matches, plot of Runs vs SR, Wickets vs ER in power play, middle and death overs, Win Probability Analysis of teams and Win Probability Contribution of players
Head-to-head tab: Detailed analysis of team-vs-team batting/bowling scorecard, batting, bowling performances, performances in power play, middle and death overs
Team performance tab: Analysis of team-vs-all other teams with batting /bowling scorecard, batting, bowling performances, performances in power play, middle and death overs
Optimisation tab: Allows one to pit batsmen vs bowlers and vice-versa. This tab also uses integer programming to optimise batting and bowling lineup
Batting analysis tab: Ranks batsmen using Runs or SR. Also plots performances of batsmen in power play, middle and death overs and plots them in a 4×4 grid
Bowling analysis tab: Ranks bowlers based on Wickets or ER. Also plots performances of bowlers in power play, middle and death overs and plots them in a 4×4 grid

Also note all these tabs and features are available for all T20 formats namely IPL, Intl. T20 (men, women), BBL, NTB, PSL, CPL, SSM.

Important note: It is possible, that at times, the Win Probability (Deep Learning) for some recent IPL matches will give an error. This is because I need to rebuild the models on a daily basis as the matches use player embeddings and there are new players. While I will definitely rebuild the models on weekends and whenever I find time, you may have to bear with this error occasionally.

Note: All charts are interactive, which means that you can hover, zoom-in, zoom-out, pan etc on the charts

The latest avatar of GooglyPlusPlus2023 is based on my R package yorkr with data from Cricsheet.

Check out the latest version of GooglyPlusPlus

Follow me on twitter for daily highlights @tvganesh_85

GooglyPlusPlus can analyse players, matches, teams, rank, compute win probability and much more.

Included below are some random analyses of IPL 2023 matches so far

A) Chennai Super Kings vs Gujarat Titans – 31 Mar 2023

GT won by 5 wickets ( 4 balls remaining)

a) Worm Wicket Chart

b) Ball-by-ball Win Probability (Logistic Regression) (side-by-side)

This model shows that CSK had the upper hand in the 2nd last over, before it changed to GT. More details on Win Probability and Win Probability Contribution in the posts given by the links above.

c) b) Ball-by-ball Win Probability (Logistic Regression) (overlapping)

Here the ball-by-ball win probability is overlapped. CSK and GT both had nearly the same probability of winning in the 2nd last over before GT edges CSK out

B) Punjab Kings vs Rajasthan Royals – 05 Apr 2023

This was a another closely fought match. PBKS won by 5 runs

a) Worm wicket chart

b) Batting partnerships

Shikhar Dhawan scored 86 runs

c) Ball-by-ball Win Probability using Deep Learning (overlapping)

PBKS was generally ahead in the win probability race

d) Batsman Win Probability Contribution

This plot shows how the different batsmen contributed to the Win Probability. We can see that Shikhar Dhawan has a highest win probability. He played a very sensible innings. Also it appears that there is no difference between Prabhsimran Singh and others, though he score 60 runs. This computation is based on when they come to bat and how the win probability changes when they get dismissed, as seen in the 2nd chart

C) Delhi Capitals vs Gujarat Titans – 4 Apr 2023

GT won by 6 wickets (11 balls remaining)

a) Worm wicket chart

b) Runs scored across 20 overs

c) Runs vs SR plot

d) Batting scorecard (Gujarat Titans)

e) Batsman Win Probability Contribution (Gujarat Titans)

Miller has a higher percentage in the Win Contribution than Sai Sudershan who held the innings together.Strange are the ways of the ML models!!

D) Sunrisers Hyderabad vs Lucknow Supergiants ( 7 Apr 2023)

LSG won by 5 wickets (24 balls left). SRH were bamboozled by the pitch while LSG was able to cruise along

a) Worm wicket chart

b) Wickets vs ER plot

c) Wickets across 20 overs

d) Ball-by-ball win probability using Deep Learning (overlapping)

e) Bowler Win Probability Contribution (LSG)

Bishnoi has a higher win probability contribution than Krunal, though he just took 1 wicket to Krunal’s 3 wickets. This is based on how the Win Probability changed at that point in the game.

The above set of plots are just a random sample.

Note: There are 8 tabs each for 9 T20 leagues (BBL, CPL, T20 (men), T20 (women), IPL, PSL, NTB, SSM, WBB). So there are a lot more detailed charts/analses.

Do take GooglyPlusPlus for a test drive!!!

Follow me on twitter @tvganesh_85 for daily highlights of previous day matches

Take a look at some of my other posts

To see all posts click Index of posts

GooglyPlusPlus: Computing T20 player’s Win Probability Contribution

In this post, I compute each batsman’s or bowler’s Win Probability Contribution (WPC) in a T20 match. This metric captures by how much the player (batsman or bowler) changed/impacted the Win Probability of the T20 match. For this computation I use my machine learning models, I had created earlier, which predicts the ball-by-ball win probability as the T20 match progresses through the 2 innings of the match.

In the picture snippet below, you can see how the win probability changes ball-by-ball for each batsman for a T20 match between CSK vs LSG- 31 Mar 2022

In my previous posts I had created several Machine Learning models. In order to compute the player’s Win Probability contribution in this post, I have used the following ML models

Logistic Regression model – glmnet : accuracy – 0.728 and roc_auc – 0.81 – Boosting Win Probability accuracy with player embeddings
Deep Learning model – DL – accuracy – 0.8639 and roc_auc – 0.946 – GooglyPlusPlus: Win Probability using Deep Learning and player embeddings

The batsman’s or bowler’s win probability contribution changes ball-by=ball. The player’s contribution is calculated as the difference in win probability when the batsman faces the 1st ball in his innings and the last ball either when is out or the innings comes to an end. If the difference is +ve the the player has had a positive impact, and likewise for negative contribution. Similarly, for a bowler, it is the win probability when he/she comes into bowl till, the last delivery he/she bowls

Note: The Win Probability Contribution does not have any relation to the how much runs or at what strike rate the batsman scored the runs. Rather the model computes different win probability for each player, based on his/her embedding, the ball in the innings and six other feature vectors like runs, run rate, runsMomentum etc. These values change for every ball as seen in the table above. Also, this is not continuous. The 2 ML models determine the Win Probability for a specific player, ball and the context in the match.

This metric is similar to Win Probability Added (WPA) used in Sabermetrics for baseball. Here is the definition of WPA from Fangraphs “Win Probability Added (WPA) captures the change in Win Expectancy from one plate appearance to the next and credits or debits the player based on how much their action increased their team’s odds of winning.” This article in Fangraphs explains in detail how this computation is done.

In this post I have added 4 new function to my R package yorkr.

batsmanWinProbLR – batsman’s win probability contribution based on glmnet (Logistic Regression)
bowlerWinProbLR – bowler’s win probability contribution based on glmnet (Logistic Regression)
batsmanWinProbDL – batsman’s win probability contribution based on Deep Learning Model
bowlerWinProbDL – bowlerWinProbLR – bowler’s win probability contribution based on Deep Learning

Hence there are 4 additional features in GooglyPlusPlus based on the above 4 functions. In addition I have also updated

-winProbLR (overLap) function to include the names of batsman when they come to bat and when they get out or the innings comes to an end, based on Logistic Regression

-winProbDL(overLap) function to include the names of batsman when they come to bat and when they get out based on Deep Learning

Hence there are 6 new features in this version of GooglyPlusPlus.

Note: All these new 6 features are available for all 9 formats of T20 in GooglyPlusPlus namely

a) IPL b) BBL c) NTB d) PSL e) Intl, T20 (men) f) Intl. T20 (women) g) WBB h) CSL i) SSM

Check out the latest version of GooglyPlusPlus at gpp2023-2

Note: The data for GooglyPlusPlus comes from Cricsheet and the Shiny app is based on my R package yorkr

A) Chennai SuperKings vs Delhi Capitals – 04 Oct 2021

To understand Win Probability Contribution better let us look at Chennai Super Kings vs Delhi Capitals match on 04 Oct 2021

This was closely fought match with fortunes swinging wildly. If we take a look at the Worm wicket chart of this match

a) Worm Wicket chart – CSK vs DC – 04 Oct 2021

Delhi Capitals finally win the match

b) Win Probability Logistic Regression (side-by-side) – CSK vs DC – 4 Oct 2021

Plotting how win probability changes over the course of the match using Logistic Regression Model

In this match Delhi Capitals won. The batting scorecard of Delhi Capitals

c) Batting Scorecard of Delhi Capitals – CSK vs DC – 4 Oct 2021

d) Win Probability Logistic Regression (Overlapping) – CSK vs DC – 4 Oct 2021

The Win Probability LR (overlapping) shows the probability function of both teams superimposed over one another. The plot includes when a batsman came into to play and when he got out. This is for both teams. This looks a little noisy, but there is a way to selectively display the change in Win Probability for each team. This can be done , by clicking the 3 arrows (orange or blue) from top to bottom. First double-click the team CSK or DC, then click the next 2 items (blue,red or black,grey) Sorry the legends don’t match the colors! 😦

Below we can see how the win probability changed for Delhi Capitals during their innings, as batsmen came into to play. See below

e) Batsman Win Probability contribution:DC – CSK vs DC – 4 Oct 2021

Computing the individual batsman’s Win Contribution and plotting we have. Hetmeyer has a higher Win Probability contribution than Shikhar Dhawan depsite scoring fewer runs

f) Bowler’s Win Probability contribution :CSK – CSK vs DC – 4 Oct 2021

We can also check the Win Probability of the bowlers. So for e.g the CSK bowlers and which bowlers had the most impact. Moeen Ali has the least impact in this match

B) Intl. T20 (men) Australia vs India – 25 Sep 2022

a) Worm wicket chart – Australia vs India – 25 Sep 2022

This was another close match in which India won with the penultimate ball

b) Win Probability based on Deep Learning model (side-by-side) – Australia vs India – 25 Sep 2022

c) Win Probability based on Deep Learning model (overlapping) – Australia vs India – 25 Sep 2022

The plot below shows how the Win Probability of the teams varied across the 20 overs. The 2 Win Probability distributions are superimposed over each other

d) Batsman Win Probability Contribution : India – Australia vs India – 25 Sep 2022

Selectively choosing the India Win Probability plot by double-clicking legend ‘India’ on the right , followed by single click of black, grey legend we have

We see that Kohli, Suryakumar Yadav have good contribution to the Win Probability

e) Plotting the Runs vs Strike Rate:India – Australia vs India – 25 Sep 2022

f) Batsman’s Win Probability Contribution- Australia vs India – 25 Sep 2022

Finally plotting the Batsman’s Win Probability Contribution

Interestingly, Kohli has a greater Win Probability Contribution than SKY, though SKY scored more runs at a better strike rate. As mentioned above, the Win Probability is context dependent and also depends on past performances of the player (batsman, bowler)

Finally let us look at

C) India vs England Intll T20 Women (11 July 2021)

a) Worm wicket chart – India vs England Intl. T20 Women (11 July 2021)

India won this T20 match by 8 runs

b) Win Probability using the Logistic Regression Model – India vs England Intl. T20 Women (11 July 2021)

c) Win Probability with the DL model – India vs England Intl. T20 Women (11 July 2021)

d) Bowler Win Probability Contribution with the LR model – India vs England Intl. T20 Women (11 July 2021)

e) Bowler Win Contribution with the DL model – India vs England Intl. T20 Women (11 July 2021)

Go ahead and try out the latest version of GooglyPlusPlus

Also see my other posts

To see all posts click Index of posts

GooglyPlusPlus: Win Probability using Deep Learning and player embeddings

In my last post ‘GooglyPlusPlus now with Win Probability Analysis for all T20 matches‘ I had discussed the performance of my ML models, created with and without player embeddings, in computing the Win Probability of T20 matches. With batsman & bowler embeddings I got much better performance than without the embeddings

glmnet – Accuracy – 0.73
Random Forest (RF) – Accuracy – 0.92

While the Random Forest gave excellent accuracy, it was bulky and also took an unusually long time to predict the Win Probability of a single T20 match. The above 2 ML models were built using R’s Tidymodels. glmnet was fast, but I wanted to see if I could create a ML model that was better, lighter and faster. I had initially tried to use Tensorflow, Keras in Python but then abandoned it, since I did not know how to port the Deep Learning model to R and use in my app GooglyPlusPlus.

But later, since I was stuck with a bulky Random Forest model, I decided to again explore options for saving the Keras Deep Learning model and loading it in R. I found out that saving the model as .h5, we can load it in R and use it for predictions. Hence, I rebuilt a Deep Learning model using Keras, Python with player embeddings and I got excellent performance. The DL model was light and had an accuracy 0.8639 with an ROC_AUC of 0.964 which was great!

GooglyPlusPlus uses data from Cricsheet and is based on my R package yorkr

You can try out this latest version of GooglyPlusPlus at gpp2023-1

Here are the steps

A. Build a Keras Deep Learning model

a. Import necessary packages

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from pathlib import Path
import matplotlib.pyplot as plt

b, Upload the data of all 9 T20 leagues (BBL, CPL, IPL, T20 (men) , T20(women), NTB, CPL, SSM, WBB)

# Read all T20 leagues 
df1=pd.read_csv('t20.csv')
print("Shape of dataframe=",df1.shape)

# Create training and test data set
train_dataset = df1.sample(frac=0.8,random_state=0)
test_dataset = df1.drop(train_dataset.index)
train_dataset1 = train_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_dataset1 = test_dataset[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
train_dataset1

# Set the target data
train_labels = train_dataset.pop('isWinner')
test_labels = test_dataset.pop('isWinner')
train_dataset1

a=train_dataset1.describe()
stats=a.transpose
a

c. Create a Deep Learning ML model using batsman & bowler embeddings

import pandas as pd
import numpy as np
from keras.layers import Input, Embedding, Flatten, Dense
from keras.models import Model
from keras.layers import Input, Embedding, Flatten, Dense, Reshape, Concatenate, Dropout
from keras.models import Model

# Set seed
tf.random.set_seed(432)

# create input layers for each of the predictors
batsmanIdx_input = Input(shape=(1,), name='batsmanIdx')
bowlerIdx_input = Input(shape=(1,), name='bowlerIdx')
ballNum_input = Input(shape=(1,), name='ballNum')
ballsRemaining_input = Input(shape=(1,), name='ballsRemaining')
runs_input = Input(shape=(1,), name='runs')
runRate_input = Input(shape=(1,), name='runRate')
numWickets_input = Input(shape=(1,), name='numWickets')
runsMomentum_input = Input(shape=(1,), name='runsMomentum')
perfIndex_input = Input(shape=(1,), name='perfIndex')

# Set the embedding size as the 4th root of unique batsmen, bowlers
no_of_unique_batman=len(df1["batsmanIdx"].unique()) 
no_of_unique_bowler=len(df1["bowlerIdx"].unique()) 
embedding_size_bat = no_of_unique_batman ** (1/4)
embedding_size_bwl = no_of_unique_bowler ** (1/4)


# create embedding layer for the categorical predictor
batsmanIdx_embedding = Embedding(input_dim=no_of_unique_batman+1, output_dim=16,input_length=1)(batsmanIdx_input)
batsmanIdx_flatten = Flatten()(batsmanIdx_embedding)
bowlerIdx_embedding = Embedding(input_dim=no_of_unique_bowler+1, output_dim=16,input_length=1)(bowlerIdx_input)
bowlerIdx_flatten = Flatten()(bowlerIdx_embedding)

# concatenate all the predictors
x = keras.layers.concatenate([batsmanIdx_flatten,bowlerIdx_flatten, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input])

# add hidden layers
# Use dropouts for regularisation
x = Dense(64, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(32, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(16, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(8, activation='relu')(x)
x = Dropout(0.1)(x)

# add output layer
output = Dense(1, activation='sigmoid', name='output')(x)
print(output.shape)

# create a DL model
model = Model(inputs=[batsmanIdx_input,bowlerIdx_input, ballNum_input, ballsRemaining_input, runs_input, runRate_input, numWickets_input, runsMomentum_input, perfIndex_input], outputs=output)
model.summary()

# compile model
optimizer=keras.optimizers.Adam(learning_rate=.01, beta_1=0.9, beta_2=0.999, epsilon=1e-07, decay=0.0, amsgrad=True)

model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=['accuracy'])

# train the model
history=model.fit([train_dataset1['batsmanIdx'],train_dataset1['bowlerIdx'],train_dataset1['ballNum'],train_dataset1['ballsRemaining'],train_dataset1['runs'],
           train_dataset1['runRate'],train_dataset1['numWickets'],train_dataset1['runsMomentum'],train_dataset1['perfIndex']], train_labels, epochs=40, batch_size=1024,
          validation_data = ([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']],test_labels), verbose=1)

plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train", "test"], loc="upper left")
plt.show()

Model: "model_5"
__________________________________________________________________________________________________
 Layer (type)                   Output Shape         Param #     Connected to                     
==================================================================================================
 batsmanIdx (InputLayer)        [(None, 1)]          0           []                               
                                                                                                  
 bowlerIdx (InputLayer)         [(None, 1)]          0           []                               
                                                                                                  
 embedding_10 (Embedding)       (None, 1, 16)        75888       ['batsmanIdx[0][0]']             
                                                                                                  
 embedding_11 (Embedding)       (None, 1, 16)        55808       ['bowlerIdx[0][0]']              
                                                                                                  
 flatten_10 (Flatten)           (None, 16)           0           ['embedding_10[0][0]']           
                                                                                                  
 flatten_11 (Flatten)           (None, 16)           0           ['embedding_11[0][0]']           
                                                                                                  
 ballNum (InputLayer)           [(None, 1)]          0           []                               
                                                                                                  
 ballsRemaining (InputLayer)    [(None, 1)]          0           []                               
                                                                                                  
 runs (InputLayer)              [(None, 1)]          0           []                               
                                                                                                  
 runRate (InputLayer)           [(None, 1)]          0           []                               
                                                                                                  
 numWickets (InputLayer)        [(None, 1)]          0           []                               
                                                                                                  
 runsMomentum (InputLayer)      [(None, 1)]          0           []                               
                                                                                                  
 perfIndex (InputLayer)         [(None, 1)]          0           []                               
                                                                                                  
 concatenate_5 (Concatenate)    (None, 39)           0           ['flatten_10[0][0]',             
                                                                  'flatten_11[0][0]',             
                                                                  'ballNum[0][0]',                
                                                                  'ballsRemaining[0][0]',         
                                                                  'runs[0][0]',                   
                                                                  'runRate[0][0]',                
                                                                  'numWickets[0][0]',             
                                                                  'runsMomentum[0][0]',           
                                                                  'perfIndex[0][0]']              
                                                                                                  
 dense_19 (Dense)               (None, 64)           2560        ['concatenate_5[0][0]']          
                                                                                                  
 dropout_19 (Dropout)           (None, 64)           0           ['dense_19[0][0]']               
                                                                                                  
 dense_20 (Dense)               (None, 32)           2080        ['dropout_19[0][0]']             
                                                                                                  
 dropout_20 (Dropout)           (None, 32)           0           ['dense_20[0][0]']               
                                                                                                  
 dense_21 (Dense)               (None, 16)           528         ['dropout_20[0][0]']             
                                                                                                  
 dropout_21 (Dropout)           (None, 16)           0           ['dense_21[0][0]']               
                                                                                                  
 dense_22 (Dense)               (None, 8)            136         ['dropout_21[0][0]']             
                                                                                                  
 dropout_22 (Dropout)           (None, 8)            0           ['dense_22[0][0]']               
                                                                                                  
 output (Dense)                 (None, 1)            9           ['dropout_22[0][0]']             
                                                                                                  
==================================================================================================
Total params: 137,009
Trainable params: 137,009
Non-trainable params: 0
__________________________________________________________________________________________________
Epoch 1/40
937/937 [==============================] - 11s 10ms/step - loss: 0.5683 - accuracy: 0.6968 - val_loss: 0.4480 - val_accuracy: 0.7708
Epoch 2/40
937/937 [==============================] - 9s 10ms/step - loss: 0.4477 - accuracy: 0.7721 - val_loss: 0.4305 - val_accuracy: 0.7833
Epoch 3/40
937/937 [==============================] - 9s 10ms/step - loss: 0.4229 - accuracy: 0.7832 - val_loss: 0.3984 - val_accuracy: 0.7936
...
...
937/937 [==============================] - 10s 10ms/step - loss: 0.2909 - accuracy: 0.8627 - val_loss: 0.2943 - val_accuracy: 0.8613
Epoch 38/40
937/937 [==============================] - 10s 10ms/step - loss: 0.2892 - accuracy: 0.8633 - val_loss: 0.2933 - val_accuracy: 0.8621
Epoch 39/40
937/937 [==============================] - 10s 10ms/step - loss: 0.2889 - accuracy: 0.8638 - val_loss: 0.2941 - val_accuracy: 0.8620
Epoch 40/40
937/937 [==============================] - 10s 11ms/step - loss: 0.2886 - accuracy: 0.8639 - val_loss: 0.2929 - val_accuracy: 0.8621

d. Compute and plot the ROC-AUC for the above model

from sklearn.metrics import roc_curve

# Select a random sample set
tf.random.set_seed(59)
train = df1.sample(frac=0.9,random_state=0)
test = df1.drop(train_dataset.index)
test_dataset1 = test[['batsmanIdx','bowlerIdx','ballNum','ballsRemaining','runs','runRate','numWickets','runsMomentum','perfIndex']]
test_labels = test.pop('isWinner')

# Compute the predicted values
y_pred_keras = model.predict([test_dataset1['batsmanIdx'],test_dataset1['bowlerIdx'],test_dataset1['ballNum'],test_dataset1['ballsRemaining'],test_dataset1['runs'],
           test_dataset1['runRate'],test_dataset1['numWickets'],test_dataset1['runsMomentum'],test_dataset1['perfIndex']]).ravel()

# Compute TPR & FPR
fpr_keras, tpr_keras, thresholds_keras = roc_curve(test_labels, y_pred_keras)

fpr_keras, tpr_keras, thresholds_keras = roc_curve(test_labels, y_pred_keras)
from sklearn.metrics import auc

# Plot the Area Under the Curve (AUC)
auc_keras = auc(fpr_keras, tpr_keras)
plt.figure(1)
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_keras, tpr_keras, label='Keras (area = {:.3f})'.format(auc_keras))
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()

The ROC_AUC for the Deep Learning Model is 0.946 as seen below

e. Save the Keras model for use in Python

from keras.models import Model
model.save("wpDL.h5")

f. Load the model in R using rhdf5 package for use in GooglyPlusPlus

library(rhdf5)
dl_model <- load_model_hdf5('wpDL.h5')

This was a huge success for me to be able to create the Deep Learning model in Python and use it in my Shiny app GooglyPlusPlus. The Deep Learning Keras model is light-weight and extremely fast.

The Deep Learning model has now been integrated into GooglyPlusPlus. Now you can check the Win Probability using both a) glmnet (Logistic Regression with lasso regularisation) b) Keras Deep Learning model with dropouts as regularisation

In addition I have created 2 features based on Win Probability (WP)

i) Win Probability (Side-by-side – Plot(interactive) : With this functionality the 1st and 2nd innings will be side-by-side. When the 1st innings is played by team 1, the Win Probability of team 2 = 100 – WP (team1). Similarly, when the 2nd innings is being played by team 2, the Win Probability of team1 = 100 – WP (team 2)

ii) Win Probability (Overlapping) – Plot (static): With this functionality the Win Probabilities of both team1(1st innings) & team 2 (2nd innings) are displayed overlapping, so that we can see how the probabilities vary ball-by-ball.

Note: Since the same UI is used for all match functions I had to re-use the Plot(interactive) and Plot(static) radio buttons for Win Probability (Side-by-side) and Win Probability(Overlapping) respectively

Here are screenshots using both ML models with both functionality for some random matches

B) ICC T20 Men World Cup – Netherland-South Africa- 2022-11-06

i) Match Worm wicket chart

ii) Win Probability with LR (Side-by-Side- Plot(interactive))

iii) Win Probability LR (Overlapping- Plot(static))

iv) Win Probability Deep Learning (Side-by-side – Plot(interactive)

In the 213th ball of the innings South Africa was slightly ahead of Netherlands. After that they crashed and burned!

v) Win Probability Deep Learning (Overlapping – Plot (static)

It can be seen that in the 94th ball of both innings South Africa was ahead of Netherlands before the eventual slump.

C) Intl. T20 (Women) India – New Zealand – 2020 – 02 – 27

Here is an interesting match between India and New Zealand T20 Women’s teams. NZ successfully chased the India’s total in a wildly swinging fortunes. See the charts below

i) Match Worm Wicket chart

ii) Win Probability with LR (Side-by-side – Plot (interactive)

iii) Win Probability with LR (Overlapping – Plot (static)

iv) Win Probability with DL model (Side-by-side – Plot (interactive))

v) Win Probability with DL model (Overlapping – Plot (static))

The above functionality in plotting the Win Probability using LR or DL with both options (Side-by-side or Overlapping) is available for all 9 T20 leagues currently supported by GooglyPlusPlus.

Go ahead and give gpp2023-1 a try!!!

Do also check out my other posts’

To see all posts click Index of posts

Boosting Win Probability accuracy with player embeddings

In my previous post Computing Win Probability of T20 matches I had discussed various approaches on computing Win Probability of T20 matches. I had created ML models with glmnet and random forest using TidyModels. This was what I had achieved

glmnet : accuracy – 0.67 and sensitivity/specificity – 0.68/0.65
random forest : accuracy – 0.737 and roc_auc- 0.834
DL model with Keras in Python : accuracy – 0.73

I wanted to see if the performance of the models could be further improved. I got a suggestion from a AI/DL whizkid, who is close to me, to include embeddings for batsmen and bowlers. He felt that win percentage is influenced by which batsman faces which bowler.

So, I started to explore this idea. Embeddings can be used to convert categorical variables to a vector of continuous floating point numbers.Fortunately R’s Tidymodels, has a convenient functionality to create embeddings. By including embeddings for batsman, bowler the performance of my ML models improved vastly. Now the performance is

glmnet : accuracy – 0.728 and roc_auc – 0.81
random forest : accuracy – 0.927 and roc_auc – 0.98
mlp-dnn :accuracy – 0.762 and roc_auc – 0.854

As can be seem there is almost a 20% increase in accuracy with random forests with embeddings over the model without embeddings. Moreover, the feature importance which is plotted below shows that the bowler and batsman embeddings have a significant influence on the Win Probability

Note: The data for this analysis is taken from Cricsheet and has been processed with my R package yorkr.

A. Win Probability using GLM with penalty and player embeddings

Here Generalised Linear Model (GLMNET) for Logistic Regression is used. In the GLMNET the regularisation path is computed for the lasso or elastic net penalty at a grid of values for the regularisation parameter lambda. glmnet is extremely fast and gave an accuracy of 0.72 for an roc_auc of 0.81 with batsman, bowler embeddings. This was good improvement over my earlier implementation with glmnet without the batsman & bowler embeddings which had a

Read the data

a) Read the data from 9 T20 leagues (BBL, CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB) and create a single data frame of ball-by-ball data. Display the data frame

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)
library(tidymodels)  
library(embed)

# Helper packages
library(readr)       # for importing data
library(vip) 

df1=read.csv("output3/matchesBBL3.csv")
df2=read.csv("output3/matchesCPL3.csv")
df3=read.csv("output3/matchesIPL3.csv")
df4=read.csv("output3/matchesNTB3.csv")
df5=read.csv("output3/matchesPSL3.csv")
df6=read.csv("output3/matchesSSM3.csv")
df7=read.csv("output3/matchesT20M3.csv")
df8=read.csv("output3/matchesT20W3.csv")
df9=read.csv("output3/matchesWBB3.csv")

#Bind all dataframes together
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)
glimpse(df)
Rows: 1,199,115
Columns: 10
$ batsman        <chr> "JD Smith", "M Klinger", "M Klinger", "M Klinger", "JD …
$ bowler         <chr> "NM Hauritz", "NM Hauritz", "NM Hauritz", "NM Hauritz",…

$ ballNum        <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, …
$ ballsRemaining <int> 125, 124, 123, 122, 121, 120, 119, 118, 117, 116, 115, …
$ runs           <int> 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 13, 14, 16, 18, 18,…

$ runRate        <dbl> 1.0000000, 0.5000000, 0.6666667, 0.7500000, 0.6000000, …
$ numWickets     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ runsMomentum   <dbl> 0.08800000, 0.08870968, 0.08943089, 0.09016393, 0.09090…
$ perfIndex      <dbl> 11.000000, 5.500000, 7.333333, 8.250000, 6.600000, 5.50…
$ isWinner       <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…


df %>% 
  count(isWinner) %>% 
  mutate(prop = n/sum(n))
  isWinner      n      prop
1        
0 614237 0.5122419
2        
1 584878 0.4877581

2) Create training.validation and test sets

b) Split to training, validation and test sets. The dataset is initially split into training and test in the ratio 80%:20%. The training data is again split into training and validation in the ratio 80:20

set.seed(123)
splits      <- initial_split(df,prop = 0.80)
splits
<Training/Testing/Total>
<959292/239823/1199115>
df_other <- training(splits)
df_test  <- testing(splits)

set.seed(234)
val_set <- validation_split(df_other,prop = 0.80)
val_set
# A tibble: 1 × 2
  splits                  
id        
  <list>                  <chr>     
1 <split [767433/191859]> validation

3) Create pre-processing recipe

a) Normalise the following predictors

ballNum
ballsRemaining
runs
runRate
numWickets
runsMomentum
perfIndex

b) Create floating point embeddings for

batsman
bowler

4) Create a Logistic Regression Workflow by adding the GLM model and the recipe

5) Create grid of elastic penalty values for regularisation

6) Train all 30 models

7) Plot the ROC of the model against the penalty

# Use all 12 cores
cores <- parallel::detectCores()
cores
# Create a Logistic Regression model with penalty
lr_mod <- 
  logistic_reg(penalty = tune(), mixture = 1) %>% 
  set_engine("glmnet",num.threads = cores)

# Create pre-processing recipe
lr_recipe <- 
  recipe(isWinner ~ ., data = df_other) %>%
  step_embed(batsman,bowler, outcome = vars(isWinner)) %>%  step_normalize(ballNum,ballsRemaining,runs,runRate,numWickets,runsMomentum,perfIndex) 

# Set the workflow by adding the GLM model with the recipe
lr_workflow <- 
  workflow() %>% 
  add_model(lr_mod) %>% 
  add_recipe(lr_recipe)

# Create a grid for the elastic net penalty
lr_reg_grid <- tibble(penalty = 10^seq(-4, -1, length.out = 30))
lr_reg_grid %>% top_n(-5) 
# A tibble: 5 × 1
   penalty
     
<dbl>
1 0.0001  
2 0.000127
3 0.000161
4 0.000204
5 0.000259

lr_reg_grid %>% top_n(5)  # highest penalty values
# A tibble: 5 × 1
  penalty
    <dbl>
1  0.0386
2  0.0489
3  0.0621
4  0.0788
5  0.1

# Train 30 penalized models
lr_res <- 
  lr_workflow %>% 
  tune_grid(val_set,
            grid = lr_reg_grid,
            control = control_grid(save_pred = TRUE),
            metrics = metric_set(accuracy,roc_auc))

# Plot the penalty versus ROC
lr_plot <- 
  lr_res %>% 
  collect_metrics() %>% 
  ggplot(aes(x = penalty, y = mean)) + 
  geom_point() + 
  geom_line() + 
  ylab("Area under the ROC Curve") +
  scale_x_log10(labels = scales::label_number())

lr_plot

The Penalty vs ROC plot is shown below

8) Display the ROC_AUC of the top models with the penalty

9) Select the model with the best ROC_AUC and the associated penalty. It can be seen the best mean ROC_AUC is 0.81 and the associated penalty is 0.000530

top_models <-
  lr_res %>% 
  show_best("roc_auc", n = 15) %>% 
  arrange(penalty) 
top_models

# A tibble: 15 × 7
    penalty .metric .estimator  mean     n std_err .config              
      <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
 1 0.0001   roc_auc binary     0.810     1      NA Preprocessor1_Model01
 2 0.000127 roc_auc binary     0.810     1      NA Preprocessor1_Model02
 3 0.000161 roc_auc binary     0.810     1      NA Preprocessor1_Model03
 4 0.000204 roc_auc binary     0.810     1      NA Preprocessor1_Model04
 5 0.000259 roc_auc binary     0.810     1      NA Preprocessor1_Model05
 6 0.000329 roc_auc binary     0.810     1      NA Preprocessor1_Model06
 7 0.000418 roc_auc binary     0.810     1      NA Preprocessor1_Model07
 8 0.000530 roc_auc binary     0.810     1      NA Preprocessor1_Model08
 9 0.000672 roc_auc binary     0.810     1      NA Preprocessor1_Model09
10 0.000853 roc_auc binary     0.810     1      NA Preprocessor1_Model10
11 0.00108  roc_auc binary     0.810     1      NA Preprocessor1_Model11
12 0.00137  roc_auc binary     0.810     1      NA Preprocessor1_Model12
13 0.00174  roc_auc binary     0.809     1      NA Preprocessor1_Model13
14 0.00221  roc_auc binary     0.809     1      NA Preprocessor1_Model14
15 0.00281  roc_auc binary     0.809     1      NA Preprocessor1_Model15

#Picking the best model and the corresponding penalty
lr_best <- 
  lr_res %>% 
  collect_metrics() %>% 
  arrange(penalty) %>% 
  slice(8)
lr_best
# A tibble: 1 × 7
   
   penalty .metric .estimator  mean     n std_err .config              
     <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                

1 0.000530 roc_auc binary     0.810     1      NA Preprocessor1_Model08

# Collect predictions and generate the AUC curve
lr_auc <- 
  lr_res %>% 
  collect_predictions(parameters = lr_best) %>% 
  roc_curve(isWinner, .pred_0) %>% 
  mutate(model = "Logistic Regression")

autoplot(lr_auc)

7) Plot the Area under the Curve (AUC).

10) Build the final model with the best LR parameters value as found in lr_best

a) The best performance was for a penalty of 0.000530

b) The accuracy achieved is 0.72. Clearly using the embeddings for batsman, bowlers improves on the performance of the GLM model without the embeddings. The accuracy achieved was 0.72 whereas previously it was 0.67 see (Computing Win Probability of T20 Matches)

c) Create a fit with the best parameters

d) The accuracy is 72.8% and the ROC_AUC is 0.813

# Create a model with the penalty for best ROC_AUC
last_lr_mod <- 
  logistic_reg(penalty = 0.000530, mixture = 1) %>% 
  set_engine("glmnet",num.threads = cores,importance = "impurity")

#Update the workflow with this model
last_lr_workflow <- 
  lr_workflow %>% 
  update_model(last_lr_mod)

#Create a fit
set.seed(345)
last_lr_fit <- 
  last_lr_workflow %>% 
  last_fit(splits)

#Generate accuracy, roc_auc
last_lr_fit %>% 
  collect_metrics()
# A tibble: 2 × 4
  .metric  .estimator .estimate .config             
  
<chr>    <chr>          <dbl> <chr>               
1 accuracy binary         0.728 Preprocessor1_Model1

2 roc_auc  binary         0.813 Preprocessor1_Model1

11) Plot the feature importance

It can be seen that bowler and batsman embeddings are the most significant for the prediction followed by runRate.

runRate –

runRate in 1st innings

requiredRunRate in 2nd innings

12) Plot the ROC characteristics

last_lr_fit %>% 
  collect_predictions() %>% 
  roc_curve(isWinner, .pred_0) %>% 
  autoplot()

13) Generate a confusion matrix

14) Create a final Generalised Linear Model for Logistic Regression with the penalty of 0.000530

15) Save the model

# generate predictions from the test set
test_predictions <- last_lr_fit %>% collect_predictions()
test_predictions

# generate a confusion matrix
test_predictions %>% 
  conf_mat(truth = isWinner, estimate = .pred_class)

Truth
Prediction     0     1
         
0                  90105 32658
         
1                  32572 84488

final_lr_model <- fit(last_lr_workflow, df_other)

final_lr_model

obj_size(final_lr_model)
146.51 MB


butcher::weigh(final_lr_model)
A tibble: 305 × 2
object                                  size
<chr>                                  <dbl>
  1 pre.actions.recipe.recipe.steps.terms1  57.9
2 pre.actions.recipe.recipe.steps.terms2  57.9
3 pre.actions.recipe.recipe.steps.terms3  57.9


cleaned_lm <- butcher::axe_env(final_lr_model, verbose = TRUE)
#✔ Memory released: "1.04 kB"
#✔ Memory released: "1.62 kB"

saveRDS(cleaned_lm, "cleanedLR.rds")

16) Compute Ball-by-ball Win Probability

Chennai Super Kings-Lucknow Super Giants-2022-03-31

16a) The corresponding Worm-wicket graph for this match is as below

Chennai Super Kings-Lucknow Super Giants-2022-03-31

B) Win Probability using Random Forest with player embeddings

In the 2nd approach I use Random Forest with batsman and bowler embeddings. The performance of the model with embeddings is quantum jump from the earlier performance without embeddings. However, the random forest is also computationally intensive.

1) Read the data

a) Read the data from 9 T20 leagues (BBL, CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB) and create a single data frame of ball-by-ball data. Display the data frame

2) Create training.validation and test sets

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)
library(tidymodels)  
library(tidymodels)  
library(embed)

# Helper packages
library(readr)       # for importing data
library(vip) 
library(ranger)

# Read all the 9 T20 leagues
df1=read.csv("output3/matchesBBL3.csv")
df2=read.csv("output3/matchesCPL3.csv")
df3=read.csv("output3/matchesIPL3.csv")
df4=read.csv("output3/matchesNTB3.csv")
df5=read.csv("output3/matchesPSL3.csv")
df6=read.csv("output3/matchesSSM3.csv")
df7=read.csv("output3/matchesT20M3.csv")
df8=read.csv("output3/matchesT20W3.csv")
df9=read.csv("output3/matchesWBB3.csv")

# Bind into a single dataframe
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)

set.seed(123)
df$isWinner = as.factor(df$isWinner)

#Split data into training, validation and test sets
splits      <- initial_split(df,prop = 0.80)
df_other <- training(splits)
df_test  <- testing(splits)
set.seed(234)
val_set <- validation_split(df_other, prop = 0.80)
val_set

2) Create a Random Forest model tuning for number of predictor nodes at each decision node (mtry) and minimum number of predictor nodes (min_n)

3) Use the ranger engine and set up for classification

4) Set up the recipe and include batsman and bowler embeddings

5) Create a workflow and add the recipe and the random forest model with the tuning parameters

# Use all 12 cores parallely
cores <- parallel::detectCores()
cores
[1] 12

# Create the random forest model with mtry and min as tuning parameters
rf_mod <- 
  rand_forest(mtry = tune(), min_n = tune(), trees = 1000) %>% 
  set_engine("ranger", num.threads = cores) %>% 
  set_mode("classification")

# Setup the recipe with batsman and bowler embeddings
rf_recipe <- 
  recipe(isWinner ~ ., data = df_other) %>% 
  step_embed(batsman,bowler, outcome = vars(isWinner)) 

# Create the random forest workflow
rf_workflow <- 
  workflow() %>% 
  add_model(rf_mod) %>% 
  add_recipe(rf_recipe)

rf_mod
# show what will be tuned
extract_parameter_set_dials(rf_mod)

set.seed(345)
# specify which values meant to tune

# Build the model
rf_res <- 
  rf_workflow %>% 
  tune_grid(val_set,
            grid = 10,
            control = control_grid(save_pred = TRUE),
            metrics = metric_set(accuracy,roc_auc))

# Pick the best  roc_auc and the associated tuning parameters
rf_res %>% 
  show_best(metric = "roc_auc")
# A tibble: 5 × 8
   mtry min_n .metric .estimator  mean     n std_err .config              
  <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
1     4     4 roc_auc binary     0.980     1      NA Preprocessor1_Model08
2     9     8 roc_auc binary     0.979     1      NA Preprocessor1_Model03

3     8    16 roc_auc binary     0.974     1      NA Preprocessor1_Model10
4     7    22 roc_auc binary     0.969     1      NA Preprocessor1_Model09

5     5    19 roc_auc binary     0.969     1      NA Preprocessor1_Model06

rf_res %>% 
  show_best(metric = "accuracy")
# A tibble: 5 × 8
   
mtry min_n .metric  .estimator  mean     n std_err .config              
  <int> <int> <chr>    <chr>      <dbl> <int>   <dbl> <chr>                
1  4     4 accuracy binary    0.927     1      NA Preprocessor1_Model08

2  9     8 accuracy binary    0.926     1      NA Preprocessor1_Model03
3  8    16 accuracy binary    0.915     1      NA Preprocessor1_Model10
4  7    22 accuracy binary    0.906     1      NA Preprocessor1_Model09

5  5    19 accuracy binary    0.904     1      NA Preprocessor1_Model0

6) Select all models with the best roc_auc. It can be seen that the best roc_auc is 0.980 for mtry=4 and min_n=4

7) Get the model with the highest accuracy. The highest accuracy achieved is 0.927 or 92.7. This accuracy is also for mtry=4 and min_n=4

# Pick the best  roc_auc and the associated tuning parameters
rf_res %>% 
  show_best(metric = "roc_auc")
# A tibble: 5 × 8
   mtry min_n .metric .estimator  mean     n std_err .config              
  <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
1     4     4 roc_auc binary     0.980     1      NA Preprocessor1_Model08
2     9     8 roc_auc binary     0.979     1      NA Preprocessor1_Model03

3     8    16 roc_auc binary     0.974     1      NA Preprocessor1_Model10
4     7    22 roc_auc binary     0.969     1      NA Preprocessor1_Model09

5     5    19 roc_auc binary     0.969     1      NA Preprocessor1_Model06

# Display the accuracy of the models in descending order and the parameters
rf_res %>% 
  show_best(metric = "accuracy")
# A tibble: 5 × 8
   
mtry min_n .metric  .estimator  mean     n std_err .config              
  <int> <int> <chr>    <chr>      <dbl> <int>   <dbl> <chr>                
1  4     4 accuracy binary    0.927     1      NA Preprocessor1_Model08

2  9     8 accuracy binary    0.926     1      NA Preprocessor1_Model03
3  8    16 accuracy binary    0.915     1      NA Preprocessor1_Model10
4  7    22 accuracy binary    0.906     1      NA Preprocessor1_Model09

5  5    19 accuracy binary    0.904     1      NA Preprocessor1_Model0

8) Select the model with the best parameters for accuracy mtry=4 and min_n=4. For this the accuracy is 0.927. For this configuration the roc_auc is also the best at 0.980

9) Plot the Area Under the Curve (AUC). It can be seen that this model performs really well and it hugs the top left.

# Pick the best model
rf_best <- 
  rf_res %>% 
  select_best(metric = "accuracy")

# The best model has mtry=4 and min=4
rf_best
     mtry min_n .config              
  <int> <int> <chr>                
1     4     4      Preprocessor1_Model08

#Plot AUC
rf_auc <- 
  rf_res %>% 
  collect_predictions(parameters = rf_best) %>% 
  roc_curve(isWinner, .pred_0) %>% 
  mutate(model = "Random Forest")

autoplot(rf_auc)

10) Create the final model with the best parameters

11) Execute the final fit

12) Plot feature importance, The bowler and batsman embedding followed by perfIndex and runRate are features that contribute the most to the Win Probability

last_rf_mod <- 
  rand_forest(mtry = 4, min_n = 4, trees = 1000) %>% 
  set_engine("ranger", num.threads = cores, importance = "impurity") %>% 
  set_mode("classification")

# the last workflow
last_rf_workflow <- 
  rf_workflow %>% 
  update_model(last_rf_mod)

set.seed(345)
last_rf_fit <- 
  last_rf_workflow %>% 
  last_fit(splits)

last_rf_fit %>% 
  collect_metrics()

  .metric  .estimator .estimate .config             
  <chr>    <chr>          <dbl> <chr>               

1 accuracy binary         0.944 Preprocessor1_Model1
2 roc_auc  binary         0.988 Preprocessor1_Model1

last_rf_fit %>% 
  extract_fit_parsnip() %>% 
  vip(num_features = 9)

13) Plot the ROC curve for the best fit

# Plot the ROC for the final model
last_rf_fit %>% 
  collect_predictions() %>% 
  roc_curve(isWinner, .pred_0) %>% 
  autoplot()

14) Create a confusion matrix

We can see that the number of false positives and false negatives is very low

15) Create the final fit with the Random Forest Model

# generate predictions from the test set
test_predictions <- last_rf_fit %>% collect_predictions()
test_predictions

   id               .pred_0 .pred_1  .row .pred_class isWinner .config          
   <chr>              <dbl>   <dbl> <int> <fct>       <fct>    <chr>            
 1 train/test split   0.838  0.162      1 0           0       Preprocessor1_Mo…
 2 
train/test split   0.463  0.537     11 1           0        Preprocessor1_Mo…
 3 
train/test split   0.846  0.154     14 0           0        Preprocessor1_Mo…
 4 
train/test split   0.839  0.161     22 0           0        Preprocessor1_Mo…
 5 
train/test split   0.846  0.154     36 0           0        Preprocessor1_Mo…
 6 
train/test split   0.848  0.152     37 0           0        Preprocessor1_Mo…
 7 
train/test split   0.731  0.269     39 0           0        Preprocessor1_Mo…
 8 
train/test split   0.972  0.0281    40 0           0        Preprocessor1_Mo…
 9 
train/test split   0.655  0.345     42 0           0        Preprocessor1_Mo…
10 
train/test split   0.662  0.338     43 0           0        Preprocessor1_Mo…

# generate a confusion matrix
test_predictions %>% 
  conf_mat(truth = isWinner, estimate = .pred_class)

          Truth
Prediction      0      1
         
          0 116576   7096
         
          1   6391 109760

# Create the final model
final_model <- fit(last_rf_workflow, df_other)

16) Computing Win Probability with Random Forest Model for match

Pakistan-India-2022-10-23

17) Worm -wicket graph of match

Pakistan-India-2022-10-23

C) Win Probability using MLP – Deep Neural Network (DNN) with player embeddings

In this approach the MLP package of Tidymodels was used. Multi-layer perceptron (MLP) with Deep Neural Network (DNN) was used to compute the Win Probability using player embeddings. An accuracy of 0.76 was obtained

1) Read the data

a) Read the data from 9 T20 leagues (BBL, CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB) and create a single data frame of ball-by-ball data. Display the data frame

2) Create training.validation and test sets

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)
library(tidymodels)    
library(embed)

# Helper packages
library(readr)       # for importing data
library(vip) 
library(ranger)

df1=read.csv("output3/matchesBBL3.csv")
df2=read.csv("output3/matchesCPL3.csv")
df3=read.csv("output3/matchesIPL3.csv")
df4=read.csv("output3/matchesNTB3.csv")
df5=read.csv("output3/matchesPSL3.csv")
df6=read.csv("output3/matchesSSM3.csv")
df7=read.csv("output3/matchesT20M3.csv")
df8=read.csv("output3/matchesT20W3.csv")
df9=read.csv("output3/matchesWBB3.csv")

df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)


set.seed(123)
df$isWinner = as.factor(df$isWinner)
splits      <- initial_split(df,prop = 0.80)
df_other <- training(splits)
df_test  <- testing(splits)
set.seed(234)
val_set <- validation_split(df_other, 
                            prop = 0.80)
val_set

3) Create a Deep Neural Network recipe

Normalize parameters
Add embeddings for batsman, bowler

4) Set the MLP-DNN hyperparameters

epochs=100
hidden units =5
dropout regularization =0.1

5) Fit on Training data

cores <- parallel::detectCores()
cores

nn_recipe <- 
  recipe(isWinner ~ ., data = df_other) %>% 
step_normalize(ballNum,ballsRemaining,runs,runRate,numWickets,runsMomentum,perfIndex) %>%
  step_embed(batsman,bowler, outcome = vars(isWinner)) %>%
  prep(training = df_other, retain = TRUE) 

# For validation:
test_normalized <- bake(nn_recipe, new_data = df_test)

set.seed(57974)
# Set the hyper parameters for DNN
# Use Keras
# Fit on training data
nnet_fit <-
  mlp(epochs = 100, hidden_units = 5, dropout = 0.1) %>%
  set_mode("classification") %>% 
  # Also set engine-specific `verbose` argument to prevent logging the results: 
  set_engine("keras", verbose = 0) %>%
  fit(isWinner ~ ., data = bake(nn_recipe, new_data = df_other))

nnet_fit
parsnip model object
Model:"sequential"

____________________________________________________________________________

Layer (type)                                           Output Shape                                    Param #            
============================================================================
dense (Dense)                                           (None, 5)                                          60                 
____________________________________________________________________________

dense_1 (Dense)                                         (None, 5)                                          30                 
____________________________________________________________________________
dropout (Dropout)                                       (None, 5)                                          0                  
____________________________________________________________________________
dense_2 (Dense)                                         (None, 2)                                          12                 
============================================================================
Total params: 102
Trainable params: 102
Non-trainable params: 0

6) Test on Test data

Check ROC_AUC. It is 0.854
Check accuracy. The MLP-DNN gives a decent performance with an acuracy of 0.76
Compute the Confusion Matrix

# Validate on test data
val_results <- 
  df_test %>%
  bind_cols(
    predict(nnet_fit, new_data = test_normalized),
    predict(nnet_fit, new_data = test_normalized, type = "prob")
  )
val_results 

# Check roc_auc
val_results %>% roc_auc(truth = isWinner, .pred_0)
  .metric .estimator .estimate
  
   <chr>   <chr>          <dbl>
1 roc_auc binary         0.854

# Check accuracy
val_results %>% accuracy(truth = isWinner, .pred_class)
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.762

# Display confusion matrix
val_results %>% conf_mat(truth = isWinner, .pred_class)
          Truth
Prediction     
           0     1        
       0 97419 31564       
       1 25548 85292

Conclusion

Of the 3 ML models, glmnet, random forest and Multi-layer Perceptron DNN, random forest had the best performance
Random Forest ML model with batsman, bowler embeddings was able to achieve an accuracy of 92.4% and a ROC_AUC of 0.98 with very low false positives, negatives. This was a quantum jump from my earlier random forest model without embeddings which had an accuracy of 73.7% and an ROC_AUC of 0.834
The glmnet and NN models are fairly light weight. Random Forest is computationally very intensive.

Check out my other posts

To see all posts click Index of posts

Computing Win-Probability of T20 matches

I am late to the ‘Win probability’ computation for T20 matches, but managed to jump on to this bus with this post. Win Probability analysis and computation have been around for some time and are used in baseball, NFL, soccer hockey and others. On T20 cricket, the following posts from White Ball Analytics & Sports Data Science were good pointers to the general approach. The data for the Win Probability computation is taken from Cricsheet.

My initial Machine Learning models could not do better than 62% accuracy. I created a data set of ~830 IPL matches which roughly came to about 280,000 rows of ball-by-ball match data but I could not move beyond 62%. Addition of T20 men moved the needle to 64% accuracy. I spent time tuning Deep Learning networks using Tensorflow and Keras. Finally, I added T20 data from 9 T20 leagues – IPL, T20 men, T20 women, BBL, CPL, NTB, PSL, WBB, SSM. I had one large data set of 1.2 million rows of ball by ball data. The data frame looks like

I created a data frame for each match from ball Num 1 to ballNum ~240 for the 1st and 2nd innings of the match. My initial set of features were ballNum, runs, runRate, numWickets. The target variable isWinner= {0,1} depending on whether the team has won or lost the match.

The features

ballNum – ball number for 1 ~ 240+ in data frame. 1 – 120+ for 1st innings and 120+ – 240+ in 2nd innings including noballs, wides etc.
runs = cumulative runs scored at the ball count
runRate = cumulative runs scored/ ballNum (for 1st innings) and runs= required runs/ball Num for 2nd innings
numWickets = wickets lost

The target variable isWinner can take values {0,1} depending whether the team won or lost

With this initial dataframe, even though I had close to 1.2 million rows of ball by ball data of T20 matches my best performance with vanilla Logistic regression & SVM in Python was about 64% accuracy.

# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB
df1=pd.read_csv('matchesT20M.csv')
df2=pd.read_csv('matchesIPL.csv')
df3=pd.read_csv('matchesBBL.csv')
df4=pd.read_csv('matchesCPL.csv')
df5=pd.read_csv('matchesNTB.csv')
df6=pd.read_csv('matchesPSL.csv')
df7=pd.read_csv('matchesSSM.csv')
df8=pd.read_csv('matchesT20W.csv')
df9=pd.read_csv('matchesWBB.csv')

# Create one large dataframe
df10=pd.concat([df1,df2,df3,df4,df5,df6,df7,df8,df9])
print("Shape of dataframe=",df10.shape)
print("#####################################")
stats=check_values(df10)
print("#####################################")
model_fit(df10)
#norm_model_fit(df,stats)
svm_model_fit(df10)

Shape of dataframe= (1206901, 6)
#####################################
Null values: False
It contains 0 infinite values

Accuracy of Logistic regression classifier on training set: 0.63
Accuracy of Logistic regression classifier on test set: 0.64
Accuracy: 0.64
Precision: 0.62
Recall: 0.65
F1: 0.64


Accuracy of Linear SVC classifier on training set: 0.52
Accuracy of Linear SVC classifier on test set: 0.52

With Tensorflow/Keras the performance was about 67%. I tried several things

Normalisation
Tried different learning rates
Different optimisers – SGD, RMSProp, Adam
Changed depth and width of Neural Network

However I did not get much improvement. Finally I decided to do some Feature engineering. I added 2 new features

a) Runs Momentum : This feature is based on the fact that more the wickets in hand, the more freely the batsmen can make risky strokes, hence increasing the momentum of the runs, This is calculated as

runsMomentum = (11 – numWickets)/balls remaining

b) Performance Index: This feature is the product of the run rate x wickets in hand. In other words, if the strike rate is good and fewer wickets lost at the point in the match, then the performance index is higher at that point in the match will be higher

The final set of features chosen were as below

I had also included the balls Remaining in the innings. Now with this set of features I decided to execute Tensorflow/Keras and do a GridSearch with different learning rates, optimisers. After a couple of hours of computation I got an accuracy of 0.73. I needed to be able to read the ML model in R which required installation of Tensorflow, reticulate and Keras in RStudio and I had several issues. Since I hit a roadblock I moved to regular R models

I performed WIn Probability computation in the following ways

A) Win Probability with Vanilla Logistic Regression (R)

With vanilla Logistic Regression in R using the ‘glm’ package I got an accuracy of 0.67, sensitivity of 0.68 and specificity of 0.65 as shown below

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)

# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB
df1=read.csv("output2/matchesBBL2.csv")
df2=read.csv("output2/matchesCPL2.csv")
df3=read.csv("output2/matchesIPL2.csv")
df4=read.csv("output2/matchesNTB2.csv")
df5=read.csv("output2/matchesPSL2.csv")
df6=read.csv("output2/matchesSSM2.csv")
df7=read.csv("output2/matchesT20M2.csv")
df8=read.csv("output2/matchesT20W2.csv")
df9=read.csv("output2/matchesWBB2.csv")

# Create one large dataframe
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)

# Helper function to split into training/test
trainTestSplit <- function(df,trainPercent,seed1){
  ## Sample size percent
  samp_size <- floor(trainPercent/100 * nrow(df))
  ## set the seed 
  set.seed(seed1)
  idx <- sample(seq_len(nrow(df)), size = samp_size)
  idx
  
}

train_idx <- trainTestSplit(df,trainPercent=80,seed=5)
train <- df[train_idx, ]

test <- df[-train_idx, ]
# Fit a generalized linear logistic model, 
fit=glm(isWinner~.,family=binomial,data=train,control = list(maxit = 50))

a=predict(fit,newdata=train,type="response")
# Set response >0.5 as 1 and <=0.5 as 0
b=as.factor(ifelse(a>0.5,1,0))
# Compute the confusion matrix for training data

confusionMatrix(
  factor(b, levels = 0:1),
  factor(train$isWinner, levels = 0:1)
)

Confusion Matrix and Statistics

          Reference
Prediction    
  0      1
         0 339938 160336
         1 154236 310217
                                         
               Accuracy : 0.6739         
                 95% CI : (0.673, 0.6749)
    No Information Rate : 0.5122         
    P-Value [Acc > NIR] : < 2.2e-16      
                                         
                  Kappa : 0.3473         
                                         
 Mcnemar's Test P-Value : < 2.2e-16      
                                         
            Sensitivity : 0.6879         
            Specificity : 0.6593         
         Pos Pred Value : 0.6795         
         Neg Pred Value : 0.6679         
             Prevalence : 0.5122         
         Detection Rate : 0.3524         
   Detection Prevalence : 0.5186         
      Balanced Accuracy : 0.6736         
                                         
       'Positive' Class : 0      

# This can be saved and loaded as    
saveRDS(fit, "glm.rds")
ml_model <- readRDS("glm.rds")

Using the above ML model on Deccan Chargers vs Chennai Super on 27-04-2009 the Win Probability as the match progresses is as below

The Worm wicket graph of this match shows it was a closely fought match

B) Win Probability using Random Forests with Tidy Models – R

Initially I tried Tidy models with tuning for glmnet. The best I got was 0.67. However, I got an excellent performance using TidyModels with Random Forests. I am using Tidy Models for the first time and I have been blown away with how logically it is constructed, much like dplyr & ggplot2.

library(dplyr)
library(caret)
library(e1071)
library(ggplot2)
library(tidymodels)  

# Helper packages
library(readr)       # for importing data
library(vip) 
library(ranger)
# Read all the data from 9 T20 leagues
# BBL,CPL, IPL, NTB, PSL, SSM, T20 Men, T20 Women, WBB

df1=read.csv("output2/matchesBBL2.csv")
df2=read.csv("output2/matchesCPL2.csv")
df3=read.csv("output2/matchesIPL2.csv")
df4=read.csv("output2/matchesNTB2.csv")
df5=read.csv("output2/matchesPSL2.csv")
df6=read.csv("output2/matchesSSM2.csv")
df7=read.csv("output2/matchesT20M2.csv")
df8=read.csv("output2/matchesT20W2.csv")
df9=read.csv("output2/matchesWBB2.csv")

# Create one large dataframe
df=rbind(df1,df2,df3,df4,df5,df6,df7,df8,df9)

dim(df)
[1] 
1205909       8

# Take a peek at the dataset
glimpse(df)
$ ballNum        <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28…
$ ballsRemaining <int> 125, 124, 123, 122, 121, 120, 119, 118, 117, 116, 115, 114, 113, 112, 111, 110, 109, 108, 107, 106, 1…
$ runs           <int> 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 13, 14, 16, 18, 18, 18, 24, 24, 24, 26, 26, 32, 32, 33, 34, 34, 3…
$ runRate        <dbl> 1.0000000, 0.5000000, 0.6666667, 0.7500000, 0.6000000, 0.5000000, 0.5714286, 0.5000000, 0.5555556, 0.…
$ numWickets     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3,…
$ runsMomentum   <dbl> 0.08800000, 0.08870968, 0.08943089, 0.09016393, 0.09090909, 0.09166667, 0.09243697, 0.09322034, 0.094…
$ perfIndex      <dbl> 11.000000, 5.500000, 7.333333, 8.250000, 6.600000, 5.500000, 6.285714, 5.500000, 6.111111, 5.000000, …
$ isWinner       <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…

df %>% 
  count(isWinner) %>% 
  mutate(prop = n/sum(n))

set.seed(123)
df$isWinner = as.factor(df$isWinner)

# Split the data into training and test set in 80%:20%
splits      <- initial_split(df,prop = 0.80)
df_other <- training(splits)
df_test  <- testing(splits)

# Create a validation set from training set in 80%:20%
set.seed(234)
val_set <- validation_split(df_other, 
                            prop = 0.80)
val_set

# Setup for Random forest using Ranger for classification
# Set up cores for parallel execution
cores <- parallel::detectCores()
cores

#Set up Random Forest engine
rf_mod <- 
  rand_forest(mtry = tune(), min_n = tune(), trees = 1000) %>% 
  set_engine("ranger", num.threads = cores) %>% 
  set_mode("classification")

rf_mod
# The Random Forest engine includes mtry which is number of predictor 
# variables required at each decision  tree with min_n the minimum number # of 
Random Forest Model Specification (classification)

Main Arguments:
  mtry = tune()
  trees = 1000
  min_n = tune()

Engine-Specific Arguments:
  num.threads = cores

Computational engine: ranger


# Setup the predictors and target variable
# Normalise all predictors. Random Forest don't need normalization but
# I have done it anyway
rf_recipe <-
  recipe(isWinner ~ ., data = df_other) %>% 
  step_normalize(all_predictors())

# Create workflow adding the ML model and recipe
rf_workflow <- 
  workflow() %>% 
  add_model(rf_mod) %>% 
  add_recipe(rf_recipe)

# The tune is done for 5 different values of the tuning parameters.
# Metrics include accuracy and roc_auc
rf_res <- 
  rf_workflow %>% 
  tune_grid(val_set,
            grid = 5,
            control = control_grid(save_pred = TRUE),
            metrics = metric_set(accuracy,roc_auc))

$ Pick the best of ROC/AUC
rf_res %>% 
  show_best(metric = "roc_auc")

We can see that when mtry (number of predictors) is 5 or 7 the ROC_AUC is 0.834 which is quite good

# A tibble: 5 × 8
   mtry min_n .metric .estimator  mean     n std_err .config             
  <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1     5    26 roc_auc binary     0.834     1      NA Preprocessor1_Model5
2     7    36 roc_auc binary     0.834     1      NA Preprocessor1_Model3
3     2    17 roc_auc binary     0.833     1      NA Preprocessor1_Model4
4     1    20 roc_auc binary     0.832     1      NA Preprocessor1_Model2
5     5     6 roc_auc binary     0.825     1      NA Preprocessor1_Model1


# Select the model with highest accuracy
rf_res %>% 
  show_best(metric = "accuracy")
   mtry min_n .metric  .estimator  mean     n std_err .config             
  <int> <int> <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1     7    36 accuracy binary     0.737     1      NA Preprocessor1_Model3
2     5    26 accuracy binary     0.736     1      NA Preprocessor1_Model5
3     1    20 accuracy binary     0.736     1      NA Preprocessor1_Model2
4     2    17 accuracy binary     0.735     1      NA Preprocessor1_Model4
5     5     6 accuracy binary     0.731     1      NA Preprocessor1_Model1

# The model with mtry (number of predictors) is 7 has the best accuracy. 
# Hence the best model has mtry=7 and min_n=36

rf_best <- 
  rf_res %>% 
  select_best(metric = "accuracy")

# Display the best model
rf_best
# A tibble: 1 × 3
   mtry min_n .config             
  <int> <int> <chr>               
1     7    36 Preprocessor1_Model3


rf_res %>% 
  collect_predictions()
   id         .pred_class  .row  mtry min_n .pred_0  .pred_1 isWinner .config             
   <chr>      <fct>       <int> <int> <int>   <dbl>    <dbl> <fct>    <chr>               
 1 validation 1               1     5     6 0.497   0.503    0        Preprocessor1_Model1
 2 validation 1               9     5     6 0.00753 0.992    1        Preprocessor1_Model1
 3 validation 0              10     5     6 0.627   0.373    0        Preprocessor1_Model1
 4 validation 0              16     5     6 0.998   0.002    0        Preprocessor1_Model1
 5 validation 1              18     5     6 0.270   0.730    1        Preprocessor1_Model1
 6 validation 0              23     5     6 0.899   0.101    0        Preprocessor1_Model1
 7 validation 1              26     5     6 0.452   0.548    1        Preprocessor1_Model1
 8 validation 0              30     5     6 0.657   0.343    1        Preprocessor1_Model1
 9 validation 0              34     5     6 0.576   0.424    0        Preprocessor1_Model1
10 validation 0              35     5     6 1.00    0.000167 0        Preprocessor1_Model1

rf_auc <- 
  rf_res %>% 
  collect_predictions(parameters = rf_best) %>% 
  roc_curve(isWinner, .pred_0) %>% 
  mutate(model = "Random Forest")

autoplot(rf_auc)

The Final Model

# Create the final Random Forest model with mtry=7 and min_n=36
# engine as "ranger" for classification
last_rf_mod <- 
  rand_forest(mtry = 7, min_n = 36, trees = 1000) %>% 
  set_engine("ranger", num.threads = cores, importance = "impurity") %>% 
  set_mode("classification")


# the last workflow is updated with the final model
last_rf_workflow <- 
  rf_workflow %>% 
  update_model(last_rf_mod)

set.seed(345)
last_rf_fit <- 
  last_rf_workflow %>% 
  last_fit(splits)

# Collect metrics
last_rf_fit %>% 
  collect_metrics()
  .metric  .estimator .estimate .config             
  <chr>    <chr>          <dbl> <chr>               
1 accuracy binary         0.739 Preprocessor1_Model1
2 roc_auc  binary         0.837 Preprocessor1_Model1

The Random Forest model gives an accuracy of 0.739 and ROC_AUC of .837 which I think is quite good. This is roughly what I got with Tensorflow/Keras

# Get the feature importance 
last_rf_fit %>% 
  extract_fit_parsnip() %>% 
  vip(num_features = 7)

Interestingly the feature that I engineered seems to have the maximum importancce namely Performance Index which is a product of Run rate x Wicket in Hand. I would have thought numWickets would be important but in T20 match probably is is not.

 generate predictions from the test set
test_predictions <- last_rf_fit %>% collect_predictions()
> test_predictions
# A tibble: 241,182 × 7
id               .pred_0 .pred_1  .row .pred_class isWinner .config             
<chr>              <dbl>   <dbl> <int> <fct>       <fct>    <chr>               
  1 train/test split   0.496   0.504     1 1           0        Preprocessor1_Model1
2 train/test split   0.640   0.360    11 0           0        Preprocessor1_Model1
3 train/test split   0.596   0.404    14 0           0        Preprocessor1_Model1
4 train/test split   0.287   0.713    22 1           0        Preprocessor1_Model1
5 train/test split   0.616   0.384    28 0           0        Preprocessor1_Model1
6 train/test split   0.516   0.484    36 0           0        Preprocessor1_Model1
7 train/test split   0.754   0.246    37 0           0        Preprocessor1_Model1
8 train/test split   0.641   0.359    39 0           0        Preprocessor1_Model1
9 train/test split   0.811   0.189    40 0           0        Preprocessor1_Model1
10 train/test split   0.618   0.382    42 0           0        Preprocessor1_Model1


# generate a confusion matrix
test_predictions %>% 
  conf_mat(truth = isWinner, estimate = .pred_class)

          Truth
Prediction     0     1
         0 92173 31623
         1 31320 86066

# Create the final model on the train/test data
final_model <- fit(last_rf_workflow, df_other)

# Final model
final_model
══ Workflow [trained] ════════════════════════════════════════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: rand_forest()

── Preprocessor ──────────────────────────────────────────────────────────────────────────────────────────────────────────────
1 Recipe Step

• step_normalize()

── Model ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Ranger result

Call:
 ranger::ranger(x = maybe_data_frame(x), y = y, mtry = min_cols(~7,      x), num.trees = ~1000, min.node.size = min_rows(~36, x),      num.threads = ~cores, importance = ~"impurity", verbose = FALSE,      seed = sample.int(10^5, 1), probability = TRUE) 

Type:                             Probability estimation 
Number of trees:                  1000 
Sample size:                      964727 
Number of independent variables:  7 
Mtry:                             7 
Target node size:                 36 
Variable importance mode:         impurity 
Splitrule:                        gini 
OOB prediction error (Brier s.):  0.1631303

The Random Forest Model’s performance has been quite impressive and probably requires further exploration.

# Saving and loading the model
save(final_model, file = "fit.rda")
load("fit.rda")

#Predicting the Win Probability of CSK vs DD match on 12 May 2012

Comparing this with the Worm wicket graph of this match we see that DD had no chance at all

C) Win Probability with Tensorflow/Keras with Grid Search – Python

I spent a fair amount of time tuning the hyper parameters of the Keras Deep Learning Network. Finally did go for the Grid Search. Incidentally I did ask ChatGPT to suggest code snippets for GridSearch which it promptly did!!!

import pandas as pd
import numpy as np
from zipfile import ZipFile
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import regularizers
from sklearn.model_selection import GridSearchCV

# Define the model
def create_model(optimizer='adam'):
    tf.random.set_seed(4)
    model = tf.keras.Sequential([
        keras.layers.Dense(32, activation=tf.nn.relu, input_shape=[len(train_dataset1.keys())]),
        keras.layers.Dense(16, activation=tf.nn.relu),
        keras.layers.Dense(8, activation=tf.nn.relu),
        keras.layers.Dense(1,activation=tf.nn.sigmoid)
    ])

    # Since this is binary classification use binary_crossentropy
    model.compile(loss='binary_crossentropy',
                    optimizer=optimizer,
                    metrics='accuracy')
    return(model)

    # Create a KerasClassifier object
model = keras.wrappers.scikit_learn.KerasClassifier(build_fn=create_model)

# Define the grid of hyperparameters to search over
batch_size = [1024]
epochs = [40]
learning_rate = [0.01, 0.001, 0.0001]
optimizer = ['SGD', 'RMSprop', 'Adagrad', 'Adadelta', 'Adam', 'Adamax', 'Nadam']

param_grid = dict(dict(optimizer=optimizer,batch_size=batch_size, epochs=epochs) )
# Create the grid search object
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=3)

# Fit the grid search object to the training data
grid_search.fit(normalized_train_data, train_labels)

# Print the best hyperparameters
print('Best hyperparameters:', grid_search.best_params_)
# summarize results
print("Best: %f using %s" % (grid_search.best_score_, grid_search.best_params_))
means = grid_search.cv_results_['mean_test_score']
stds = grid_search.cv_results_['std_test_score']
params = grid_search.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

The best worked out to be the optimiser ‘Nadam’ with a learning rate of 0.001

import matplotlib.pyplot as plt
# Create a model
tf.random.set_seed(4)
model = tf.keras.Sequential([
    keras.layers.Dense(32, activation=tf.nn.relu, input_shape=[len(train_dataset1.keys())]),
    keras.layers.Dense(16, activation=tf.nn.relu),
    keras.layers.Dense(8, activation=tf.nn.relu),
    keras.layers.Dense(1,activation=tf.nn.sigmoid)
  ])

# Use the Nadam optimiser
optimizer=keras.optimizers.Nadam(learning_rate=.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, decay=0.0)

# Since this is binary classification use binary_crossentropy
model.compile(loss='binary_crossentropy',
                optimizer=optimizer,
                metrics='accuracy')

# Fit 
#history=model.fit(
#  train_dataset1, train_labels,batch_size=1024,
#  epochs=40, validation_data=(test_dataset1,test_labels), verbose=1)
history=model.fit(
  normalized_train_data, train_labels,batch_size=1024,
  epochs=40, validation_data=(normalized_test_data,test_labels), verbose=1)

Epoch 37/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4971 - accuracy: 0.7310 - val_loss: 0.4968 - val_accuracy: 0.7357
Epoch 38/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4970 - accuracy: 0.7310 - val_loss: 0.4974 - val_accuracy: 0.7378
Epoch 39/40
943/943 [==============================] - 4s 4ms/step - loss: 0.4970 - accuracy: 0.7309 - val_loss: 0.4994 - val_accuracy: 0.7296
Epoch 40/40
943/943 [==============================] - 3s 3ms/step - loss: 0.4969 - accuracy: 0.7311 - val_loss: 0.4998 - val_accuracy: 0.7300
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train", "test"], loc="upper left")
plt.show()

Conclusion

So, the Keras Deep Learning Network gives about the same performance of Random Forest in Tidy Models. But I went with R Random Forest as it was easier to save and load the model for use with my data. Also, I am not sure whether the performance of the ML model can be improved beyond a point. However, I will continue to explore.

Watch this space!!!

Also see

To see all posts click Index of posts

References

Near Real-time Analytics of ICC Men’s T20 World Cup with GooglyPlusPlus

In my last post GooglyPlusPlus gets ready for ICC Men’s T20 World Cup, I had mentioned that GooglyPlusPlus was preparing for the big event the ICC Men’s T20 World cup. Now that the T20 World cup is underway, my Shiny app in R, GooglyPlusPlus ,will be generating near real-time analytics of matches completed the previous day. Besides the app can also do historical analysis of players, teams and matches.

The whole process is automated. A cron job will execute every day, in the morning, which will automatically download the matches of the previous day from Cricsheet, unzip them, start a pipeline which will transform and process the match data into necessary folders and finally upload the newly acquired data into my Shiny app. Hence, you will be able to access all the breathless, pulsating cricketing action in timeless, interactive plots and tables which will capture all aspects of Men’s T20 matches, namely batsman, bowler performance, match analysis, team-vs-team, team-vs-all teams besides ranking of batsmen & bowlers. Since the data is cumulative, all the analytics are historical and current.

Check out GooglyPlusPlus!!

The data for GooglyPlusPlus is taken from Cricsheet

Interest in cricket, has mushroomed in recent times around the world, with the addition of new formats which started with ODI, T20, T10, 100 ball and so on. There are leagues which host these matches at different levels around the world. While GooglyPlusPlus, provides near real-time analytics of Men’s T20 World cup, we can clearly envision a big data platform which ingests matches daily from multiple cricket formats, leagues around the world generating real-time and near real-time analytics which are essential these days to selection of teams at different levels through auctions. For more discussion on this see my posts

We could imagine a Data Lake, into which are ingested data from the different cricket formats, leagues through appropriate technology connectors. Once the data is ingested, we could have data pipelines, based on Azure ADF, Apache NiFi, Apache Airflow or Amazon EMR etc., to transform, process and enhance the data, generating real-time analytics on the fly. Recent formats like T20, T10 require more urgency in strategic thinking based on scoring within limited overs, or containing batsmen from going on a rampage within the set of overs, the analytics on a fly may help the coach to modify the batting or bowling lineup at points in match. In this context see my earlier post Using Linear Programming (LP) for optimizing bowling change or batting lineup in T20 cricket

All of these are not just possible, but are likely to become reality as more and more formats, leagues and cricket data proliferate around the world.

This post, focuses on generating near-real time analytics for ICC Men’s T20 World Cup using GooglyPlusPlus. Included below, is a sampling of the analytics that you can perform for analysing the matches. In addition you can do all the analysis included in my post GooglyPlusPlus gets ready for ICC Men’s T20 World Cup

Namibia-Sri Lanka-16 Oct 2022 : Match Worm graph

The opening match between Namibia vs Sri Lanka resulted in an upset. We can see this in the match worm-wicket graph below

2. Scotland vs West Indies – 17 Oct 2022: Batsmen vs Bowlers

George Munsey was the top scorer for Scotland and was instrumental in the win against WI. His performance against West Indies bowlers is shown below. Note, the charts are interactive

3. Zimbabwe vs Ireland – 17 Oct 2022 : Team Runs vs SR

Sikander Raza of Zimbabwe with 82 runs with the strike rate ~ 170

4. United Arab Emirates vs Netherlands – 16 Oct 2022: Team runs across 20 overs

UAE pipped Netherlands in the middle overs and were able to win by 1 ball and 3 wickets

5. Scotland vs Ireland – 19 Oct 2022 : Team Runs vs SR Middle overs plot

Curtis Campher snatched the game away from Scotland with his stellar performance in middle and death overs

6. UAE vs Namibia : 20 Oct 2022 : Team Wickets vs ER plot

Basoor Hameed and Zahoor Khan got 2 wickets apiece with an economy rate of ~5.00 but still they were not able to stop UAE from stealing a win

7. Overall Runs vs SR in T20 World Cup 2022

It is too early to rank the players, nevertheless in the current T20 World Cup, MP O’Dowd (Netherlands), BKG Mendis (Sri Lanka) and JN Frylinck(Namibia) are the top 3 batsmen with good runs and Strike Rate

8. Overall Wickets over ER in T20 World Cup 2022

The top 3 bowlers so far in T20 World Cup 2022 are a) BFW de Leede (Netherlands) b) PWH De Silva (Sri Lanka) c) KP Meiyappan (UAE) with a total of 7,7, and 6 wickets respectively

Note: Besides the match analysis GooglyPlusPlus also provides detailed analysis of batsmen, bowlers, matches as above, team-vs-team, team-vs-all teams, ranking of batsmen & bowlers etc. For more details see my post GooglyPlusPlus gets ready for ICC Men’s T20 World Cup

Do visit GooglyPlusPlus everyday to check out the cricketing actions of matches gone by. You can also follow me on twitter @tvganesh_85 for daily highlights.

Then, Now(IPL 2022), Beyond : Insights from GooglyPlusPlus

IPL 2022 has just concluded and yet again, it is has thrown a lot of promising and potential youngsters in its wake, while established players have fallen! With IPL 2022, we realise that “Sceptre and Crown must tumble down” and that ‘the glories‘ of form and class like everything else are “shadows not substantial things” (Death the Leveller by James Shirley).

So King Kohli had to kneel, and hitman’ himself got hit. Rishabh Pant, Jadeja also had a poor season. On the contrary there were several youngsters who shone like Abhishek Sharma, Tilak Verma, Umran Malik or a Mohsin Khan

This post is about my potential T20 Indian players for the World Cup 2022 and beyond.

The post below includes my own analysis and thoughts. Feel free to try out my Shiny app GooglyPlusPlus and draw your own conclusions.

You can also view the analyais as a youtube video at Insights from GooglyPlusPlus

How often we hear that data by itself is useless, unless we can draw insights from it? This is a prevailing theme in the corporate world and everybody uses all sorts of tools to analyse and subsequently draw insights. Data analysis can be done in many ways as data can be sliced, diced, chopped in a zillion ways. There are many facets and perspectives to analysing data. Creating insights is easy, but arriving at actionable insights is anything but. So, the problem of selecting the best 11 is difficult as there are so many ways to look at the analysis. My Shiny app GooglyPlusPlus based on my R package yorkr can analyse data in several ways namely

Batsman analysis
Bowler analysis
Match analysis
Team vs team analysis
Team vs all teams analysis
Batsman vs bowler and vice versa
Analysis of in 3,4,5 in power play, middle and death overs

GooglyPlusPlus uses my R package yorkr which has ~ 160 functions some which have several options. So, we can say roughly there are ~500 different ways that analysis can be done or in other words we can gather almost roughly 500+ different insights, not to mention that there are so many combinations of head-on matches and one-vs-all matches.

So generating insights or different ways of analysis data alone is not enough. The question is whether we can get a consolidated view from the different insights. In this post, I try to identify the best contenders for the Indian T20 team. This is far more difficult than it looks. Do you select players on past historical performance or do you choose from the newer crop of players, who have excelled in the recent IPL season. I think this boils down the typical situation in any domain. In engineering, we have tradeoffs – processing power vs memory tradeoff, throughput vs latency tradeoff or in the financial domain it is cost vs benefit or risk vs reward tradeoff. For team selection, the quandary is, whether to choose seasoned players with good historical performance but a poor performances in recent times or go with youngsters who have played with great courage and flair in this latest episode of IPL 2022. Hence there is a tradeoff between reliable but below average performance or risky but superlative performances of new players.

For this I base my potential list from

Then (past history of batsmen & bowlers) – I have chosen the performance of batsmen and bowlers in the last 3 years. With we can arrive at those who have had reasonably reliable performance for the last 3 years
Now (IPL 2022) – Performance in the current season IPL 2022

A. Then (Jan 2020 – May 2022) – Batsmen analysis

In this section I analyse the performances of batsmen and bowlers from Jan 2022 – May 2022. This is done based on ranking, and plots of Runs vs Strike Rate in Power Play, Middle and Death overs

Also I analyse bowlers based on the overall rank from Jan 2022- May 2022. Further more analysis is done on Wickets vs Economy Rate overall and in Power Play, Middle and Death overs

a. Ranks of batsmen (Runs over Strike Rate) : Jan 2020 – May 2022

The top batsmen consistency wise

[KL Rahul, Shikhar Dhawan, Ruturaj Gaikwad, Ishan Kishan, Shubman Gill, Suryakumar Yadav, Sanju Samson, Mayank Agarwal, Prithvi Shaw, Devdutt Padikkal, Nitish Rana, Virat Kohli, Shreyas Iyer, Ambati Rayadu, Rahul Tripathi, Rishabh Pant, Rohit Sharma, Hardik Pandya]

b. Ranks of batsmen (Strike Rate over Runs) : Jan 2020 – May 2022

The most consistent players from the Strike Rate perspective are

The batsmen with best Strike Rate in the last 3 years are

[Dinesh Karthik, Prithvi Shaw, Hardik Pandya, Rishabh Pant, Sanju Samson, Rahul Tripathi, Suryakumar Yadav, Nitish Rana, Mayank Agarwal, Krunal Pandya, MS Dhoni, Shikhar Dhawan, Ishan Kishan, KL Rahul]

c.Best Batsmen Runs vs SR : Jan 2020 – May 2022

The best batsmen should have a reasonable combination of Runs and SR. The best batsmen are

[KL Rahul, Shikhar Dhawan, Ruturaj Gaikwad, Ishan Kishan, Shubman Gill , Sanju Samson, Suryakumar Yadav, Shubman Gill, Mayank Agarwal, Prithvi Shaw, Nitish Rana, Hardik Pandya, Rishabh Pant, Rahul Tripathi,

d. Best batsmen Runs vs SR in Powerplay: Jan 2020 – May 2022

The best players in Power play

The best players in Power play in the last 3 years are

[KL Rahul, Prithvi Shaw, Rohit Sharma, Devdutt Padikkal, Mayank Agarwal, Virat Kohli, Ishan Kishan, Yashashvi Jaiswal, Wriddhiman Saha, Rahul Tripathi, Sanju Samson, Robin Uthappa, Venkatesh Iyer, Nitish Rana,Suryakumar Yadav, Abhishek Sharma Shreyas Iyer ]

e. Best batsmen Runs vs SR in Middleovers: Jan 2020 – May 2022

The most consistent players in the last 3 years in the middle overs are

[KL Rahul, Sanju Samson, Shikhar Dhawan, Rishabh Pant, Nitish Rana, Shreyas Iyer, Shubman Gill, Ishan Kishan, Devdutt Padikkal, Rahul Tripathi, Ruturaj Gaikwad, Shivam Dube, Hardik Pandya]

f. Best batsmen Runs vs SR in Death overs: Jan 2020 – May 2022

The best batsmen in death overs are

[Dinesh Karthik, Ravindra Jadeja, Hardik Pandya, Rahul Tewatia, MS Dhoni, KL Rahul, Rishabh Pant, Suryakumar Yadav, Ambati Rayadu, Virat Kohli, Nitish Rana, Shikhar Dhawan, Ruturaj Gaikwad, Ishan Kishan]

B) Now (IPL 2022) – Batsmen analysis

IPL 2022 just finished and clearly brings out the batsmen who are in great nick. It is always going to be a judgment call of whether to go for ‘old reliable’ or ‘new and awesome’.

a. Ranks of batsmen (Runs over Strike Rate) : IPL 2022

The best batsmen this season in Runs over Strike rate are

The best batsmen are

[KL Rahul, Shikhar Dhawan, Hardik Pandya, Deepak Hooda, Shubman Gill, Rahul Tripathi, Abhishek Sharma, Ishan Kishan, Wriddhiman Saha, Shreyas Iyer, Tilak Verma, Ruturaj Gaikwad, Sanju Samson, Shivam Dube]

b. Ranks of batsmen (Strike Rate over Runs) : IPL 2022

The batsmen with the best strike rate are

[Dinesh Karthik, Rishabh Pant, Rahul Tewathia, Rahul Tripathi, Sanju Samson, R Ashwin, Deepak Hooda, MS Dhoni, Nitish Rana, Riyan Parag, Shreya Iyer]

c.Best Batsmen Runs vs SR :IPL 2022

From an overall performance the following batsmen shone this season

[KL Rahul, Shikhar Dhawan, Shubman Gill, Hardik Pandya, Abhishel Sharma, Deepak Hooda, Rahul Tripathi, Tilak Verma, Shreya Iyer, Nitish Rana, Sanju Samson, Rishabh Pant]

d. Best batsmen Runs vs SR in Powerplay: IPL 2022

Top batsmen in Power play in IPL 2022

[Abhishek Sharma, Shikhar Dhawan, Rohit Sharma, Ishan Kishan, Shubman Gill, Prithvi Shaw, Wriddhiman Saha, Ishan Kishan, KL Rahul, Ruturaj Gaikwad, Virat Kohli, Yashasvi Jaiswal, Mayank Agarwal, Robin Uthappa, Sanju Samson, Nitish Rana]

e. Best batsmen Runs vs SR in Middleovers: IPL 2022

Best batsmen in middle overs in IPL 2022

[Deepak Hooda, Hardik Pandya, Tilak Verma, KL Rahul, Sanju Samson, Rishabh Pant, Shubman Gill, Ambati Rayudu, Suryaprakash Yadav, Shikhar Dhawan, Ruturaj Gaikwad]

f. Best batsmen Runs vs SR in Death overs: IPL 2022

Top batsmen in death overs in IPL 2022

[Dinesh Karthik, Rahul Tewatia, MS Dhoni, KL Rahul, Azar Patel, Washington Sundar, R Ashwin, Hardik Pandya, Ayush Badoni, Shivam Dube, Suryakumar Yadav, Ravindra Jadeja, Sanju Samson]

Overall Batting Performance in season

Kohli peaked in 2016 and from then on it has been a downward slide (see below)

Taking a look at Kohli’s moving average it is clear that he is past his prime and it will take a herculean effort to regain his lost glory

Similarly, Rohit Sharma’s moving average is constantly around ~30 as seen below

The cumulative average of Rohit Sharma is shown below

Comparing KL Rahul, Shikhar Dhawan, Rohit Sharma and V Kohli we see that KL Rahul and Shikhar Dhawan have had a much superior performance in the last 2-3 years. Rohit has averaged about ~25 runs every season.

Comparing the 4 wicket-keeper batsmen Sanju Samson, Rishabh Pant, Ishan Kishan and Dinesh Karthik from 2016

i) Runs over Strike Rate

We see that Pant peaked in 2018 but has not performed as well since. In the last 2 years Sanju Samson and Ishan Kishan have done well

ii) Strike Rate over Runs

For the last couple of seasons Rishabh Pant and Dinesh Kartik top the strike rate over the other 2

Similar analysis can be done other combinations of batsmen

Choosing the best batsmen from the above, my top 5 batsmen would be

KL Rahul
Shikhar Dhawan
Prithvi Shaw, Ruturaj Gaikwad, Ishan Kishan
Sanju Samson, Shreyas Iyer, Shubman Gill, Shivam Dube,
Abhishek Sharma, Tilak Verma, Rahul Tripathi, Suryakumar Yadav, Deepak Hooda
Rishabh Pant, Dinesh Karthik

Personally, I feel Ishan Kishan and Shreyas Iyer are a little tardy while playing express speeds, as compared to Sanju Samson or Rishabh Pant.

If you notice, I have not included both Virat Kohli or Rohit Sharma who have been below par for some time

C. Then (Jan 2020 – May 2022) – Bowler analysis

This section I analyse the performances of bowlers from Jan 2022 – May 2022. This is done based on ranking, and plots of Wickets vs Economy Rate in Power Play, Middle and Death overs

a. Ranks of bowlers (Wickets over Economy Rate) : Jan 2020 – May 2022

The most consistent bowlers Wickets over Economy Rate for the last 3 years are

[YS Chahal, Jasprit Bumrah, Mohammed Dhami, Harshal Patel, Shardul Thakur, Arshdeep Singh, Rahul Chahar, Varun Chakravarthy, Ravi Bishnoi, Prasidh Krishna, R Ashwon, Axar Patel, Mohammed Siraj, Ravindra Jadeja, Krunal Pandya, Rahul Tewatia]

b. Ranks of bowlers (Economy Rate over Wickets) : Jan 2020 – May 2022

The most economical bowlers since 2020 are

[Axar Patel, Krunal Pandya, Jasprit Bumrah, CV Varun, R Ashwin, Ravi Bishnoi, Rahul Chahar, YS Chahal, Ravindra Jadeja, Harshal Patel, Mohammed Shami, Mohammed Siraj, Rahul Tewatia, Arshdeep Singh, Prasidh Krishna, Shardul Thakur]

c.Best Bowlers Wickets vs ER : Jan 2020 – May 2022

The best bowlers Wickets vs ER will be in the bottom right quadrant. The most consistent and reliable bowlers are

[YS Chahal, Jasprit Bumrah, Mohammed Shami, Harshal Patel, CV Arun, Ravi Bishnoi, Rahul Chahar, R Ashwin, Axar Patel]

d. Best bowlers Wickets vs ER in Powerplay: Jan 2020 – May 2022

The best bowlers in Powerplay are

[Mohammed Shami, Deepak Chahar, Mohammed Siraj, Arshdeep Singh, Jasprit Bumrah, Avesh Khan, Mukesh Choudhary, Shardul Thakur, T Natarajan, Bhuvaneshwar Kumar, WashingtonSundar, Shivam Mavi]

e. Best bowlers Wickets vs ER in Middle overs : Jan 2020 – May 2022

The most reliable performers in middle overs from 2020-2022 are

[YS Chahal, Rahul Chahr, Ravi Bishnoi, Harshal Patel, Axar Patel, Jasprit Bumrah, Umran Malik, R Ashwin, Avesh Khan, Shardul Thakur, Kuldeep Yadav]

f. Best bowlers Wickets vs ER in Death overs : Jan 2020 – May 2022

The most reliable bowlers are

[Harshal Patel, Mohammed Shami, Jasprit Bumrah, Arshdeep Singh, T Natarajan, Avesh Khan, Shardul Thakur, Bhuvaneshwar Kumar, Shivam Mavi, YS Chahal, Prasidh Krishna, Mohammed Siraj, Chetan Sakariya]

B) Now (IPL 2022) – Bowler analysis

a. Ranks of bowlers (Wickets over Economy Rate) : IPL 2022

The best bowlers in IPL 2022 when considering Wickets over Economy Rate

[YS Chahal, Umran Malik, Prasidh Krishna, Mohammed Shami, Kuldeep Yadav, Harshal Patel, T Natarajan, Avesh Khan, Shardul Thakur, Mukesh Choudhary, Jasprit Bumrah, Ravi Bishnoi]

a. Ranks of bowlers (Economy Rate over Wickets) : IPL 2022

The most economical bowlers in IPL 2022 are

[Axar Patel, Jasprit Bumrah, Krunal Pandya, Umesh Yadav, Bhuvaneshwar Kumar, Rahul Chahr, Harshal Patel, Arshdeep Singh, R Ashwion, Umran Malik, Kuldeep Yadav, YS Chahal, Mohammed Shami, Avesh Khan, Prasidh Krishna]

c.Best Bowlers Wickets vs ER : IPL 2022

The overall best bowlers in IPL 2022 are

[YS Chahal, Umran Malik, Harshal Patel, Prasidh Krishna, Mohammed Shami, Kuldeep Yadav, Avesh Khan, Jasprit Bumrah, Umesh Yadav, Bhuvaneshwar Kumar, Arshdeep Singh, R Ashwin, Rahul Chahar, Krunal Pandya]

d. Best bowlers Wickets vs ER in Powerplay: IPL 2022

The best bowlers in IPL 2022 in Power play are

[Mukesh Choudhary, Mohammed Shami, Prasidh Krishna, Umesh Yadav, Avesh Khan, Mohsin Khan, T Natarajan, Jasprit Bumrah, Yash Dayal, Mohammed Siraj]

d. Best bowlers Wickets vs ER in Middle overs: IPL 2022

The best bowlers in IPL 2022 during middle overs

The best bowlers are

[YS Chahal, Umran Malik, Kuldeep Yadav, Harshal Patel, Ravi Bishnoi, R Ashwin]

e. Best bowlers Wickets vs ER in Death overs: IPL 2022

The best bowlers in death overs in IPL 2022 are

[T Natarajan, Harshal Patel, Bhuvaneshwar Kumar, Mohammed Shami, Jasprit Bumrah, Shardul Thakur, YS Chahal, Prasidh Krishna, Avesh Khan, Mohsin Khan, Yash Dayal, Umran Malik, Arshdeep Singh]

Typically in a team we would need a combination of 4 bowlers (2 fast & 2 spinner or 3 fast and 1 spinner) with an additional player who is all rounder.

For 4 bowlers we could have

JJ Bumrah
Mohammed Shami, Umran Malik, Bhuvaneshwar Kumar, Umesh Yadav
Arshdeep Singh, Avesh Khan, Mohsin Khan, Harshal Patel
YS Chahal, Ravi Bishnoi, Rahul Chahar, Axar Patel
Ravindra Jadeja, Hardik Pandya, Rahul Tewathia, R Ashwin

i) Performance comparison (Wickets over Economy Rate)

Bumrah had the best season in 2020. He has been doing quite well and has been among the wickets

ii) Performance comparison (Economy Rate over Wickets)

Bumrah has the best Economy Rate

We can do a wicket prediction of bowlers. So for example for Bumrah it is

iii) Performance evaluation (Wickets over Economy Rate)

Harshal Patel followed by Avesh Khan had a good season last year, but Umran Malik pipped them this year (see below)

iv) Performance analysis of spinners

a. Wickets over Economy Rate: 2022

Chahal has the best season followed by Bishnoi and Chahar this season

b) Economy Rate over WIckets

Axar Patel has the best economy rate followed by Rahul Chahar

Conclusion

The above post identified the best candidates for the Indian team in the future and beyond. In my T20 list, I have neither included Virat Kohli or Rohit Sharma. The data in T20 clearly indicates that they have had their days. There is a lot more talent around. The tradeoff is a little risk for a greater potential performance. My list would be

KL Rahul
Shikhar Dhawan
Ruturaj Gaikwad, Prithvi Shaw, Rahul Tripathi
Suryakumar Yadav, Shreyas Iyer, Abhishek Sharma, Deepak Hooda
Sanju Samson (Wicket keeper/captain)/ Rishabh Pant/Dinesh Karthik
Hardik Pandya, Ravindra Jadeja, Rahul Tewathia
Jasprit Bumrah
Mohammed Shami, Bhuvaneshwar Kumar, Umran Malik
Arshdeep Singh, Avesh Khan, Harshal Patel
YS Chahal
Axar Patel, Ravi Bishnoi, Rahul Chahar

You may agree/ disagree with my list. Feel free to do your analysis with GooglyPlusPlus and come to your own conclusions

This analysis is also available on youtube Insights from GooglyPlusPlus

Player Performance Estimation using AI Collaborative Filtering

1. Introduction

Often times before crucial matches, or in general, we would like to know the performance of a batsman against a bowler or vice-versa, but we may not have the data. We generally have data where different batsmen would have faced different sets of bowlers with certain performance data like ballsFaced, totalRuns, fours, sixes, strike rate and timesOut. Similarly different bowlers would have performance figures(deliveries, runsConceded, economyRate and wicketTaken) against different sets of batsmen. We will never have the data for all batsmen against all bowlers. However, it would be good estimate the performance of batsmen against a bowler, even though we do not have the performance data. This could be done using collaborative filtering which identifies and computes based on the similarity between batsmen vs bowlers & bowlers vs batsmen.

This post shows an approach whereby we can estimate a batsman’s performance against bowlers even though the batsman may not have faced those bowlers, based on his/her performance against other bowlers. It also estimates the performance of bowlers against batsmen using the same approach. This is based on the recommender algorithm which is used to recommend products to customers based on their rating on other products.

This idea came to me while generating the performance of batsmen vs bowlers & vice-versa for 2 IPL teams in this IPL 2022 with my Shiny app GooglyPlusPlus in the optimization tab, I found that there were some batsmen for which there was no data against certain bowlers, probably because they are playing for the first time in their team or because they were new (see picture below)

In the picture above there is no data for Dewald Brevis against Jasprit Bumrah and YS Chahal. Wouldn’t be great to estimate the performance of Brevis against Bumrah or vice-versa? Can we estimate this performance?

While pondering on this problem, I realized that this problem formulation is similar to the problem formulation for the famous Netflix movie recommendation problem, in which user’s ratings for certain movies are known and based on these ratings, the recommender engine can generate ratings for movies not yet seen.

This post estimates a player’s (batsman/bowler) using the recommender engine This post is based on R package recommenderlab

“Michael Hahsler (2021). recommenderlab: Lab for Developing and Testing Recommender Algorithms. R package version 0.2-7. https://github.com/mhahsler/recommenderlab”

Note 1: Thw data for this analysis is taken from Cricsheet after being processed by my R package yorkr.

You can also read this post in RPubs at Player Performance Estimation using AI Collaborative Filtering

A PDF copy of this post is available at Player Performance Estimation using AI Collaborative Filtering.pdf

You can download this R Markdown file and the associated data and perform the analysis yourself using any other recommender engine from Github at playerPerformanceEstimation

Problem statement

In the table below we see a set of bowlers vs a set of batsmen and the number of times the bowlers got these batsmen out.
By knowing the performance of the bowlers against some of the batsmen we can use collaborative filter to determine the missing values. This is done using the recommender engine.

The Recommender Engine works as follows. Let us say that there are feature vectors $x^1$ , $x^2$ and $x^3$ for the 3 bowlers which identify the characteristics of these bowlers (“fast”, “lateral drift through the air”, “movement off the pitch”). Let each batsman be identified by parameter vectors $\theta^1$ , $\theta^2$ and so on

For e.g. consider the following table

Then by assuming an initial estimate for the parameter vector $\theta$ and the feature vector xx we can formulate this as an optimization problem which tries to minimize the error for $\theta^T*x$ This can work very well as the algorithm can determine features which cannot be captured. So for e.g. some particular bowler may have very impressive figures. This could be due to some aspect of the bowling which cannot be captured by the data for e.g. let’s say the bowler uses the ‘scrambled seam’ when he is most effective, with a slightly different arc to the flight. Though the algorithm cannot identify the feature as we know it, but the ML algorithm should pick up intricacies which cannot be captured in data.

Hence the algorithm can be quite effective.

Note: The recommender lab performance is not very good and the Mean Square Error is quite high. Also, the ROC and AUC curves show that not in aLL cases the algorithm is doing a clean job of separating the True positives (TPR) from the False Positives (FPR)

Note: This is similar to the recommendation problem

The collaborative optimization object can be considered as a minimization of both $\theta$ and the features x and can be written as

J( $x^{(1)},x^{(2)},..x^{(n_{u})}$ , $\theta^{(1)},\theta^{(2)},..,\theta^{(n_{m})}$ }= 1/2 $\sum(\theta^{j})^{T}x^{i}- y^{(i,j)})^{2} + \lambda\sum\sum (x_{k}^{i})^{2} + \lambda\sum\sum (_\theta{k}^{j})^{2}$

The collaborative filtering algorithm can be summarized as follows

Initialize $\theta^1$ , $\theta^2$ … $\theta^{n_{u}}$ and the set of features be $x^1$ , $x^2$ , … , $x^{n_{m}}$ to small random values
Minimize J( $\theta^1$ , $\theta^2$ … $\theta^{n_{u}}$ , $x^1$ , $x^2$ , … , $x^{n_{m}}$ ) using gradient descent. For every
j=1,2, … $n_{u}$ , i= 1,2,.., $n_{m}$
$x_{k}^{i}$ := $x_{k}^{i}$ – $\alpha$ ( $\sigma$ $(\theta^j)^T$ ) $x^i$ – $y^(i,j)\theta_{k}^{j} + \lambda x_{k}^i$

&

$\theta_{k}^{i}$ := $\theta_{k}^{i}$ – $\alpha$ ( $\sigma$ $(\theta^j)^T)x^i - y^(i,j)\theta_{k}^{j} + \lambda x_{k}^i$
Hence for a batsman with parameters $\theta$ and a bowler with (learned) features x, predict the “times out” for the player where the value is not known using $\theta^Tx$

The above derivation for the recommender problem is taken from Machine Learning by Prof Andrew Ng at Coursera from the lecture Collaborative filtering

There are 2 main types of Collaborative Filtering(CF) approaches

User based Collaborative Filtering User-based CF is a memory-based algorithm which tries to mimics word-of-mouth by analyzing rating data from many individuals. The assumption is that users with similar preferences will rate items similarly.
Item based Collaborative Filtering Item-based CF is a model-based approach which produces recommendations based on the relationship between items inferred from the rating matrix. The assumption behind this approach is that users will prefer items that are similar to other items they like.

1a. A note on ROC and Precision-Recall curves

A small note on interpreting ROC & Precision-Recall curves in the post below

ROC Curve: The ROC curve plots the True Positive Rate (TPR) against the False Positive Rate (FPR). Ideally the TPR should increase faster than the FPR and the AUC (area under the curve) should be close to 1

Precision-Recall: The precision-recall curve shows the tradeoff between precision and recall for different threshold. A high area under the curve represents both high recall and high precision, where high precision relates to a low false positive rate, and high recall relates to a low false negative rate

library(reshape2)
library(dplyr)
library(ggplot2)
library(recommenderlab)
library(tidyr)
load("recom_data/batsmenVsBowler20_22.rdata")

2. Define recommender lab helper functions

Helper functions for the RMarkdown notebook are created

eval – Gives details of RMSE, MSE and MAE of ML algorithm
evalRecomMethods – Evaluates different recommender methods and plot the ROC and Precision-Recall curves

# This function returns the error for the chosen algorithm and also predicts the estimates
# for the given data
eval <- function(data, train1, k1,given1,goodRating1,recomType1="UBCF"){
  set.seed(2022)
  e<- evaluationScheme(data,
                       method = "split",
                       train = train1,
                       k = k1,
                       given = given1,
                       goodRating = goodRating1)
  
  r1 <- Recommender(getData(e, "train"), recomType1)
  print(r1)
  
  p1 <- predict(r1, getData(e, "known"), type="ratings")
  print(p1)
  
  error = calcPredictionAccuracy(p1, getData(e, "unknown"))
  
  print(error)
  p2 <- predict(r1, data, type="ratingMatrix")
  p2
}
# This function will evaluate the different recommender algorithms and plot the AUC and ROC curves
evalRecomMethods <- function(data,k1,given1,goodRating1){
  set.seed(2022)
  e<- evaluationScheme(data,
                       method = "cross",
                       k = k1,
                       given = given1,
                       goodRating = goodRating1)
  
  models_to_evaluate <- list(
    `IBCF Cosinus` = list(name = "IBCF", 
                          param = list(method = "cosine")),
    `IBCF Pearson` = list(name = "IBCF", 
                          param = list(method = "pearson")),
    `UBCF Cosinus` = list(name = "UBCF",
                          param = list(method = "cosine")),
    `UBCF Pearson` = list(name = "UBCF",
                          param = list(method = "pearson")),
    `Zufälliger Vorschlag` = list(name = "RANDOM", param=NULL)
  )
  
  n_recommendations <- c(1, 5, seq(10, 100, 10))
  list_results <- evaluate(x = e, 
                           method = models_to_evaluate, 
                           n = n_recommendations)
  plot(list_results, annotate=c(1,3), legend="bottomright")
  plot(list_results, "prec/rec", annotate=3, legend="topleft")
}

3. Batsman performance estimation

The section below regenerates the performance for batsmen based on incomplete data for the different fields in the data frame namely balls faced, fours, sixes, strike rate, times out. The recommender lab allows one to test several different algorithms all at once namely

User based – Cosine similarity method, Pearson similarity
Item based – Cosine similarity method, Pearson similarity
Popular
Random
SVD and a few others

3a. Batting dataframe

head(df)

##   batsman1         bowler1 ballsFaced totalRuns fours sixes  SR timesOut
## 1 A Badoni        A Mishra          0         0     0     0 NaN        0
## 2 A Badoni        A Nortje          0         0     0     0 NaN        0
## 3 A Badoni         A Zampa          0         0     0     0 NaN        0
## 4 A Badoni     Abdul Samad          0         0     0     0 NaN        0
## 5 A Badoni Abhishek Sharma          0         0     0     0 NaN        0
## 6 A Badoni      AD Russell          0         0     0     0 NaN        0

3b Data set and data preparation

For this analysis the data from Cricsheet has been processed using my R package yorkr to obtain the following 2 data sets – batsmenVsBowler – This dataset will contain the performance of the batsmen against the bowler and will capture a) ballsFaced b) totalRuns c) Fours d) Sixes e) SR f) timesOut – bowlerVsBatsmen – This data set will contain the performance of the bowler against the difference batsmen and will include a) deliveries b) runsConceded c) EconomyRate d) wicketsTaken

Obviously many rows/columns will be empty

This is a large data set and hence I have filtered for the period > Jan 2020 and < Dec 2022 which gives 2 datasets a) batsmanVsBowler20_22.rdata b) bowlerVsBatsman20_22.rdata

I also have 2 other datasets of all batsmen and bowlers in these 2 dataset in the files c) all-batsmen20_22.rds d) all-bowlers20_22.rds

You can download the data and this RMarkdown notebook from Github at PlayerPerformanceEstimation

Feel free to download and analyze the data and use any recommendation engine you choose

3c. Exploratory analysis

Initially an exploratory analysis is done on the data

df3 <- select(df, batsman1,bowler1,timesOut)
df6 <- xtabs(timesOut ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
print(df8[1:10,1:10])

##                 A Mishra A Nortje A Zampa Abdul Samad Abhishek Sharma
## A Badoni              NA       NA      NA          NA              NA
## A Manohar             NA       NA      NA          NA              NA
## A Nortje              NA       NA      NA          NA              NA
## AB de Villiers        NA        4       3          NA              NA
## Abdul Samad           NA       NA      NA          NA              NA
## Abhishek Sharma       NA       NA      NA          NA              NA
## AD Russell             1       NA      NA          NA              NA
## AF Milne              NA       NA      NA          NA              NA
## AJ Finch              NA       NA      NA          NA               3
## AJ Tye                NA       NA      NA          NA              NA
##                 AD Russell AF Milne AJ Tye AK Markram Akash Deep
## A Badoni                NA       NA     NA         NA         NA
## A Manohar               NA       NA     NA         NA         NA
## A Nortje                NA       NA     NA         NA         NA
## AB de Villiers           3       NA      3         NA         NA
## Abdul Samad             NA       NA     NA         NA         NA
## Abhishek Sharma         NA       NA     NA         NA         NA
## AD Russell              NA       NA      6         NA         NA
## AF Milne                NA       NA     NA         NA         NA
## AJ Finch                NA       NA     NA         NA         NA
## AJ Tye                  NA       NA     NA         NA         NA

The dots below represent data for which there is no performance data. These cells need to be estimated by the algorithm

set.seed(2022)
r <- as(df8,"realRatingMatrix")
getRatingMatrix(r)[1:15,1:15]

## 15 x 15 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 15 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                               
## A Badoni         . . . . . . . . . . . . . . .
## A Manohar        . . . . . . . . . . . . . . .
## A Nortje         . . . . . . . . . . . . . . .
## AB de Villiers   . 4 3 . . 3 . 3 . . . 4 3 . .
## Abdul Samad      . . . . . . . . . . . . . . .
## Abhishek Sharma  . . . . . . . . . . . 1 . . .
## AD Russell       1 . . . . . . 6 . . . 3 3 3 .
## AF Milne         . . . . . . . . . . . . . . .
## AJ Finch         . . . . 3 . . . . . . 1 . . .
## AJ Tye           . . . . . . . . . . . 1 . . .
## AK Markram       . . . 3 . . . . . . . . . . .
## AM Rahane        9 . . . . 3 . 3 . . . 3 3 . .
## Anmolpreet Singh . . . . . . . . . . . . . . .
## Anuj Rawat       . . . . . . . . . . . . . . .
## AR Patel         . . . . . . . 1 . . . . . . .

r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:15,1:15]

## 15 x 15 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 15 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                              
## AB de Villiers  . 4 3 . . 3 . 3 . . . 4 3 . .
## Abdul Samad     . . . . . . . . . . . . . . .
## Abhishek Sharma . . . . . . . . . . . 1 . . .
## AD Russell      1 . . . . . . 6 . . . 3 3 3 .
## AJ Finch        . . . . 3 . . . . . . 1 . . .
## AM Rahane       9 . . . . 3 . 3 . . . 3 3 . .
## AR Patel        . . . . . . . 1 . . . . . . .
## AT Rayudu       2 . . . . . 1 . . . . 3 . . .
## B Kumar         3 . 3 . . . . . . . . . . 3 .
## BA Stokes       . . . . . . 3 4 . . . 3 . . .
## CA Lynn         . . . . . . . 9 . . . 3 . . .
## CH Gayle        . . . . . 6 . 3 . . . 6 . . .
## CH Morris       . 3 . . . . . . . . . 3 . . .
## D Padikkal      . 4 . . . 3 . . . . . . 3 . .
## DA Miller       . . . . . 3 . . . . . 3 . . .

# Get the summary of the data
summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   3.000   3.000   3.463   4.000  21.000

# Normalize the data
r0_m <- normalize(r0)
getRatingMatrix(r0_m)[1:15,1:15]

## 15 x 15 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 15 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                                                       
## AB de Villiers   .         -0.7857143 -1.7857143 .  .       -1.7857143
## Abdul Samad      .          .          .         .  .        .        
## Abhishek Sharma  .          .          .         .  .        .        
## AD Russell      -2.6562500  .          .         .  .        .        
## AJ Finch         .          .          .         . -0.03125  .        
## AM Rahane        4.6041667  .          .         .  .       -1.3958333
## AR Patel         .          .          .         .  .        .        
## AT Rayudu       -2.1363636  .          .         .  .        .        
## B Kumar          0.3636364  .          0.3636364 .  .        .        
## BA Stokes        .          .          .         .  .        .        
## CA Lynn          .          .          .         .  .        .        
## CH Gayle         .          .          .         .  .        1.5476190
## CH Morris        .          0.3500000  .         .  .        .        
## D Padikkal       .          0.6250000  .         .  .       -0.3750000
## DA Miller        .          .          .         .  .       -0.7037037
##                                                                              
## AB de Villiers   .         -1.7857143 . . . -0.7857143 -1.785714  .         .
## Abdul Samad      .          .         . . .  .          .         .         .
## Abhishek Sharma  .          .         . . . -1.6000000  .         .         .
## AD Russell       .          2.3437500 . . . -0.6562500 -0.656250 -0.6562500 .
## AJ Finch         .          .         . . . -2.0312500  .         .         .
## AM Rahane        .         -1.3958333 . . . -1.3958333 -1.395833  .         .
## AR Patel         .         -2.3333333 . . .  .          .         .         .
## AT Rayudu       -3.1363636  .         . . . -1.1363636  .         .         .
## B Kumar          .          .         . . .  .          .         0.3636364 .
## BA Stokes       -0.6086957  0.3913043 . . . -0.6086957  .         .         .
## CA Lynn          .          5.3200000 . . . -0.6800000  .         .         .
## CH Gayle         .         -1.4523810 . . .  1.5476190  .         .         .
## CH Morris        .          .         . . .  0.3500000  .         .         .
## D Padikkal       .          .         . . .  .         -0.375000  .         .
## DA Miller        .          .         . . . -0.7037037  .         .         .

4. Create a visual representation of the rating data before and after the normalization

The histograms show the bias in the data is removed after normalization

r0=r[(m=rowCounts(r) > 10),]
getRatingMatrix(r0)[1:15,1:10]

## 15 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                    
## AB de Villiers  . 4 3 . . 3 . 3 . .
## Abdul Samad     . . . . . . . . . .
## Abhishek Sharma . . . . . . . . . .
## AD Russell      1 . . . . . . 6 . .
## AJ Finch        . . . . 3 . . . . .
## AM Rahane       9 . . . . 3 . 3 . .
## AR Patel        . . . . . . . 1 . .
## AT Rayudu       2 . . . . . 1 . . .
## B Kumar         3 . 3 . . . . . . .
## BA Stokes       . . . . . . 3 4 . .
## CA Lynn         . . . . . . . 9 . .
## CH Gayle        . . . . . 6 . 3 . .
## CH Morris       . 3 . . . . . . . .
## D Padikkal      . 4 . . . 3 . . . .
## DA Miller       . . . . . 3 . . . .

#Plot ratings
image(r0, main = "Raw Ratings")

#Plot normalized ratings
r0_m <- normalize(r0)
getRatingMatrix(r0_m)[1:15,1:15]

## 15 x 15 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 15 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                                                       
## AB de Villiers   .         -0.7857143 -1.7857143 .  .       -1.7857143
## Abdul Samad      .          .          .         .  .        .        
## Abhishek Sharma  .          .          .         .  .        .        
## AD Russell      -2.6562500  .          .         .  .        .        
## AJ Finch         .          .          .         . -0.03125  .        
## AM Rahane        4.6041667  .          .         .  .       -1.3958333
## AR Patel         .          .          .         .  .        .        
## AT Rayudu       -2.1363636  .          .         .  .        .        
## B Kumar          0.3636364  .          0.3636364 .  .        .        
## BA Stokes        .          .          .         .  .        .        
## CA Lynn          .          .          .         .  .        .        
## CH Gayle         .          .          .         .  .        1.5476190
## CH Morris        .          0.3500000  .         .  .        .        
## D Padikkal       .          0.6250000  .         .  .       -0.3750000
## DA Miller        .          .          .         .  .       -0.7037037
##                                                                              
## AB de Villiers   .         -1.7857143 . . . -0.7857143 -1.785714  .         .
## Abdul Samad      .          .         . . .  .          .         .         .
## Abhishek Sharma  .          .         . . . -1.6000000  .         .         .
## AD Russell       .          2.3437500 . . . -0.6562500 -0.656250 -0.6562500 .
## AJ Finch         .          .         . . . -2.0312500  .         .         .
## AM Rahane        .         -1.3958333 . . . -1.3958333 -1.395833  .         .
## AR Patel         .         -2.3333333 . . .  .          .         .         .
## AT Rayudu       -3.1363636  .         . . . -1.1363636  .         .         .
## B Kumar          .          .         . . .  .          .         0.3636364 .
## BA Stokes       -0.6086957  0.3913043 . . . -0.6086957  .         .         .
## CA Lynn          .          5.3200000 . . . -0.6800000  .         .         .
## CH Gayle         .         -1.4523810 . . .  1.5476190  .         .         .
## CH Morris        .          .         . . .  0.3500000  .         .         .
## D Padikkal       .          .         . . .  .         -0.375000  .         .
## DA Miller        .          .         . . . -0.7037037  .         .         .

image(r0_m, main = "Normalized Ratings")

set.seed(1234)
hist(getRatings(r0), breaks=25)

hist(getRatings(r0_m), breaks=25)

4a. Data for analysis

The data frame of the batsman vs bowlers from the period 2020 -2022 is read as a dataframe. To remove rows with very low number of ratings(timesOut, SR, Fours, Sixes etc), the rows are filtered so that there are at least more 10 values in the row. For the player estimation the dataframe is converted into a wide-format as a matrix (m x n) of batsman x bowler with each of the columns of the dataframe i.e. timesOut, SR, fours or sixes. These different matrices can be considered as a rating matrix for estimation.

A similar approach is taken for estimating bowler performance. Here a wide form matrix (m x n) of bowler x batsman is created for each of the columns of deliveries, runsConceded, ER, wicketsTaken

5. Batsman’s times Out

The code below estimates the number of times the batsmen would lose his/her wicket to the bowler. As discussed in the algorithm above, the recommendation engine will make an initial estimate features for the bowler and an initial estimate for the parameter vector for the batsmen. Then using gradient descent the recommender engine will determine the feature and parameter values such that the over Mean Squared Error is minimum

From the plot for the different algorithms it can be seen that UBCF performs the best. However the AUC & ROC curves are not optimal and the AUC> 0.5

df3 <- select(df, batsman1,bowler1,timesOut)
df6 <- xtabs(timesOut ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
# Filter only rows where the row count is > 10
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                    
## AB de Villiers  . 4 3 . . 3 . 3 . .
## Abdul Samad     . . . . . . . . . .
## Abhishek Sharma . . . . . . . . . .
## AD Russell      1 . . . . . . 6 . .
## AJ Finch        . . . . 3 . . . . .
## AM Rahane       9 . . . . 3 . 3 . .
## AR Patel        . . . . . . . 1 . .
## AT Rayudu       2 . . . . . 1 . . .
## B Kumar         3 . 3 . . . . . . .
## BA Stokes       . . . . . . 3 4 . .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   3.000   3.000   3.463   4.000  21.000

# Evaluate the different plotting methods
evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

#Evaluate the error
a=eval(r0[1:dim(r0)[1]],0.8,k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 70 users.
## 18 x 145 rating matrix of class 'realRatingMatrix' with 1755 ratings.
##     RMSE      MSE      MAE 
## 2.069027 4.280872 1.496388

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
m=as(c,"data.frame")
names(m) =c("batsman","bowler","TimesOut")

6. Batsman’s Strike rate

This section deals with the Strike rate of batsmen versus bowlers and estimates the values for those where the data is incomplete using UBCF method.

Even here all the algorithms do not perform too efficiently. I did try out a few variations but could not lower the error (suggestions welcome!!)

df3 <- select(df, batsman1,bowler1,SR)
df6 <- xtabs(SR ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                                                           
## AB de Villiers   96.8254 171.4286  33.33333  . 66.66667 223.07692   .     
## Abdul Samad       .      228.0000   .        .  .       100.00000   .     
## Abhishek Sharma 150.0000   .        .        .  .        66.66667   .     
## AD Russell      111.4286   .        .        .  .         .         .     
## AJ Finch        250.0000 116.6667   .        . 50.00000  85.71429 112.5000
## AJ Tye            .        .        .        .  .         .       100.0000
## AK Markram        .        .        .       50  .         .         .     
## AM Rahane       121.1111   .        .        .  .       113.82979 117.9487
## AR Patel        183.3333   .      200.00000  .  .       433.33333   .     
## AT Rayudu       126.5432 200.0000 122.22222  .  .       105.55556   .     
##                                
## AB de Villiers  109.52381 .   .
## Abdul Samad       .       .   .
## Abhishek Sharma   .       .   .
## AD Russell      195.45455 .   .
## AJ Finch          .       .   .
## AJ Tye            .       .   .
## AK Markram        .       .   .
## AM Rahane        33.33333 . 200
## AR Patel        171.42857 .   .
## AT Rayudu       204.76190 .   .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   5.882  85.714 116.667 128.529 160.606 600.000

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

a=eval(r0[1:dim(r0)[1]],0.8, k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 105 users.
## 27 x 145 rating matrix of class 'realRatingMatrix' with 3220 ratings.
##       RMSE        MSE        MAE 
##   77.71979 6040.36508   58.58484

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
n=as(c,"data.frame")
names(n) =c("batsman","bowler","SR")

7. Batsman’s Sixes

The snippet of code estimes the sixes of the batsman against bowlers. The ROC and AUC curve for UBCF looks a lot better here, as it significantly greater than 0.5

df3 <- select(df, batsman1,bowler1,sixes)
df6 <- xtabs(sixes ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                      
## AB de Villiers  3 3 . . . 18 .  3 . .
## AD Russell      3 . . . .  . . 12 . .
## AJ Finch        2 . . . .  . .  . . .
## AM Rahane       7 . . . .  3 1  . . .
## AR Patel        4 . 3 . .  6 .  1 . .
## AT Rayudu       5 2 . . .  . .  1 . .
## BA Stokes       . . . . .  . .  . . .
## CA Lynn         . . . . .  . .  9 . .
## CH Gayle       17 . . . . 17 .  . . .
## CH Morris       . . 3 . .  . .  . . .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    3.00    3.00    4.68    6.00   33.00

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

## Timing stopped at: 0.003 0 0.002

a=eval(r0[1:dim(r0)[1]],0.8, k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 52 users.
## 14 x 145 rating matrix of class 'realRatingMatrix' with 1634 ratings.
##      RMSE       MSE       MAE 
##  3.529922 12.460350  2.532122

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
o=as(c,"data.frame")
names(o) =c("batsman","bowler","Sixes")

8. Batsman’s Fours

The code below estimates 4s for the batsmen

df3 <- select(df, batsman1,bowler1,fours)
df6 <- xtabs(fours ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                      
## AB de Villiers   . 1 . . . 24 . 3 . .
## Abhishek Sharma  . . . . .  . . . . .
## AD Russell       1 . . . .  . . 9 . .
## AJ Finch         . 1 . . .  3 2 . . .
## AK Markram       . . . . .  . . . . .
## AM Rahane       11 . . . .  8 7 . . 3
## AR Patel         . . . . .  . . 3 . .
## AT Rayudu       11 2 3 . .  6 . 6 . .
## BA Stokes        1 . . . .  . . . . .
## CA Lynn          . . . . .  . . 6 . .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   3.000   4.000   6.339   9.000  55.000

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

## Timing stopped at: 0.008 0 0.008

## Warning in .local(x, method, ...): 
##   Recommender 'UBCF Pearson' has failed and has been removed from the results!

a=eval(r0[1:dim(r0)[1]],0.8, k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 67 users.
## 17 x 145 rating matrix of class 'realRatingMatrix' with 2083 ratings.
##      RMSE       MSE       MAE 
##  5.486661 30.103447  4.060990

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
p=as(c,"data.frame")
names(p) =c("batsman","bowler","Fours")

9. Batsman’s Total Runs

The code below estimates the total runs that would have scored by the batsman against different bowlers

df3 <- select(df, batsman1,bowler1,totalRuns)
df6 <- xtabs(totalRuns ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                          
## A Badoni         .  . . . .   . .   . . .
## A Manohar        .  . . . .   . .   . . .
## A Nortje         .  . . . .   . .   . . .
## AB de Villiers  61 36 3 . 6 261 .  69 . .
## Abdul Samad      . 57 . . .  12 .   . . .
## Abhishek Sharma  3  . . . .   6 .   . . .
## AD Russell      39  . . . .   . . 129 . .
## AF Milne         .  . . . .   . .   . . .
## AJ Finch        15  7 . . 3  18 9   . . .
## AJ Tye           .  . . . .   . 4   . . .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    9.00   24.00   41.36   54.00  452.00

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given1=7,goodRating1=median(getRatings(r0)))

a=eval(r0[1:dim(r0)[1]],0.8, k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 105 users.
## 27 x 145 rating matrix of class 'realRatingMatrix' with 3256 ratings.
##       RMSE        MSE        MAE 
##   41.50985 1723.06788   29.52958

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
q=as(c,"data.frame")
names(q) =c("batsman","bowler","TotalRuns")

10. Batsman’s Balls Faced

The snippet estimates the balls faced by batsmen versus bowlers

df3 <- select(df, batsman1,bowler1,ballsFaced)
df6 <- xtabs(ballsFaced ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Mishra', 'A Nortje', 'A Zampa' ... ]]

##                                         
## A Badoni         .  . . . .   . .  . . .
## A Manohar        .  . . . .   . .  . . .
## A Nortje         .  . . . .   . .  . . .
## AB de Villiers  63 21 9 . 9 117 . 63 . .
## Abdul Samad      . 25 . . .  12 .  . . .
## Abhishek Sharma  2  . . . .   9 .  . . .
## AD Russell      35  . . . .   . . 66 . .
## AF Milne         .  . . . .   . .  . . .
## AJ Finch         6  6 . . 6  21 8  . . .
## AJ Tye           .  . . . .   9 4  . . .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    9.00   18.00   30.21   39.00  384.00

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

a=eval(r0[1:dim(r0)[1]],0.8, k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 112 users.
## 28 x 145 rating matrix of class 'realRatingMatrix' with 3378 ratings.
##       RMSE        MSE        MAE 
##   33.91251 1150.05835   23.39439

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
r=as(c,"data.frame")
names(r) =c("batsman","bowler","BallsFaced")

11. Generate the Batsmen Performance Estimate

This code generates the estimated dataframe with known and ‘predicted’ values

a1=merge(m,n,by=c("batsman","bowler"))
a2=merge(a1,o,by=c("batsman","bowler"))
a3=merge(a2,p,by=c("batsman","bowler"))
a4=merge(a3,q,by=c("batsman","bowler"))
a5=merge(a4,r,by=c("batsman","bowler"))
a6= select(a5, batsman,bowler,BallsFaced,TotalRuns,Fours, Sixes, SR,TimesOut)
head(a6)

##          batsman          bowler BallsFaced TotalRuns Fours Sixes  SR TimesOut
## 1 AB de Villiers        A Mishra         94       124     7     5 144        5
## 2 AB de Villiers        A Nortje         26        42     4     3 148        3
## 3 AB de Villiers         A Zampa         28        42     5     7 106        4
## 4 AB de Villiers Abhishek Sharma         22        28     0    10 136        5
## 5 AB de Villiers      AD Russell         70       135    14    12 207        4
## 6 AB de Villiers        AF Milne         31        45     6     6 130        3

12. Bowler analysis

Just like the batsman performance estimation we can consider the bowler’s performances also for estimation. Consider the following table

As in the batsman analysis, for every batsman a set of features like (“strong backfoot player”, “360 degree player”,“Power hitter”) can be estimated with a set of initial values. Also every bowler will have an associated parameter vector θθ. Different bowlers will have performance data for different set of batsmen. Based on the initial estimate of the features and the parameters, gradient descent can be used to minimize actual values {for e.g. wicketsTaken(ratings)}.

load("recom_data/bowlerVsBatsman20_22.rdata")

12a. Bowler dataframe

Inspecting the bowler dataframe

head(df2)

##    bowler1        batsman1 balls runsConceded       ER wicketTaken
## 1 A Mishra        A Badoni     0            0 0.000000           0
## 2 A Mishra       A Manohar     0            0 0.000000           0
## 3 A Mishra        A Nortje     0            0 0.000000           0
## 4 A Mishra  AB de Villiers    63           61 5.809524           0
## 5 A Mishra     Abdul Samad     0            0 0.000000           0
## 6 A Mishra Abhishek Sharma     2            3 9.000000           0

names(df2)

## [1] "bowler1"      "batsman1"     "balls"        "runsConceded" "ER"          
## [6] "wicketTaken"

13. Balls bowled by bowler

The below section estimates the balls bowled for each bowler. We can see that UBCF Pearson and UBCF Cosine both perform well

df3 <- select(df2, bowler1,batsman1,balls)
df6 <- xtabs(balls ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Badoni', 'A Manohar', 'A Nortje' ... ]]

##                                          
## A Mishra        . . .  63  .  2 35 .  6 .
## A Nortje        . . .  21 25  .  . .  6 .
## A Zampa         . . .   9  .  .  . .  . .
## Abhishek Sharma . . .   9  .  .  . .  6 .
## AD Russell      . . . 117 12  9  . . 21 9
## AF Milne        . . .   .  .  .  . .  8 4
## AJ Tye          . . .  63  .  . 66 .  . .
## Akash Deep      . . .   .  .  .  . .  . .
## AR Patel        . . . 188  5  1 84 . 29 5
## Arshdeep Singh  . . .   6  6 24 18 . 12 .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    9.00   18.00   29.61   36.00  384.00

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

a=eval(r0[1:dim(r0)[1]],0.8,k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 96 users.
## 24 x 195 rating matrix of class 'realRatingMatrix' with 3954 ratings.
##      RMSE       MSE       MAE 
##  30.72284 943.89294  19.89204

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
s=as(c,"data.frame")
names(s) =c("bowler","batsman","BallsBowled")

14. Runs conceded by bowler

This section estimates the runs conceded by the bowler. The UBCF Cosinus algorithm performs the best with TPR increasing fastewr than FPR

df3 <- select(df2, bowler1,batsman1,runsConceded)
df6 <- xtabs(runsConceded ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Badoni', 'A Manohar', 'A Nortje' ... ]]

##                                            
## A Mishra        . . .  61  .  3  41 . 15  .
## A Nortje        . . .  36 57  .   . .  8  .
## A Zampa         . . .   3  .  .   . .  .  .
## Abhishek Sharma . . .   6  .  .   . .  3  .
## AD Russell      . . . 276 12  6   . . 21  .
## AF Milne        . . .   .  .  .   . . 10  4
## AJ Tye          . . .  69  .  . 138 .  .  .
## Akash Deep      . . .   .  .  .   . .  .  .
## AR Patel        . . . 205  5  . 165 . 33 13
## Arshdeep Singh  . . .  18  3 51  51 .  6  .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    9.00   24.00   41.34   54.00  458.00

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

## Timing stopped at: 0.004 0 0.004

## Warning in .local(x, method, ...): 
##   Recommender 'UBCF Pearson' has failed and has been removed from the results!

a=eval(r0[1:dim(r0)[1]],0.8,k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 95 users.
## 24 x 195 rating matrix of class 'realRatingMatrix' with 3820 ratings.
##       RMSE        MSE        MAE 
##   43.16674 1863.36749   30.32709

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
t=as(c,"data.frame")
names(t) =c("bowler","batsman","RunsConceded")

15. Economy Rate of the bowler

This section computes the economy rate of the bowler. The performance is not all that good

df3 <- select(df2, bowler1,batsman1,ER)
df6 <- xtabs(ER ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Badoni', 'A Manohar', 'A Nortje' ... ]]

##                                                                       
## A Mishra        . . .  5.809524  .     9.00  7.028571 . 15.000000  .  
## A Nortje        . . . 10.285714 13.68  .     .        .  8.000000  .  
## A Zampa         . . .  2.000000  .     .     .        .  .         .  
## Abhishek Sharma . . .  4.000000  .     .     .        .  3.000000  .  
## AD Russell      . . . 14.153846  6.00  4.00  .        .  6.000000  .  
## AF Milne        . . .  .         .     .     .        .  7.500000  6.0
## AJ Tye          . . .  6.571429  .     .    12.545455 .  .         .  
## Akash Deep      . . .  .         .     .     .        .  .         .  
## AR Patel        . . .  6.542553  6.00  .    11.785714 .  6.827586 15.6
## Arshdeep Singh  . . . 18.000000  3.00 12.75 17.000000 .  3.000000  .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.3529  5.2500  7.1126  7.8139  9.8000 36.0000

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

## Timing stopped at: 0.003 0 0.004

## Warning in .local(x, method, ...): 
##   Recommender 'UBCF Pearson' has failed and has been removed from the results!

a=eval(r0[1:dim(r0)[1]],0.8,k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 95 users.
## 24 x 195 rating matrix of class 'realRatingMatrix' with 3839 ratings.
##      RMSE       MSE       MAE 
##  4.380680 19.190356  3.316556

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
u=as(c,"data.frame")
names(u) =c("bowler","batsman","EconomyRate")

16. Wickets Taken by bowler

The code below computes the wickets taken by the bowler versus different batsmen

df3 <- select(df2, bowler1,batsman1,wicketTaken)
df6 <- xtabs(wicketTaken ~ ., df3)
df7 <- as.data.frame.matrix(df6)
df8 <- data.matrix(df7)
df8[df8 == 0] <- NA
r <- as(df8,"realRatingMatrix")
r0=r[(rowCounts(r) > 10),]
getRatingMatrix(r0)[1:10,1:10]

## 10 x 10 sparse Matrix of class "dgCMatrix"

##    [[ suppressing 10 column names 'A Badoni', 'A Manohar', 'A Nortje' ... ]]

##                                   
## A Mishra       . . . . . . 1 . . .
## A Nortje       . . . 4 . . . . . .
## A Zampa        . . . 3 . . . . . .
## AD Russell     . . . 3 . . . . . .
## AJ Tye         . . . 3 . . 6 . . .
## AR Patel       . . . 4 . 1 3 . 1 1
## Arshdeep Singh . . . 3 . . 3 . . .
## AS Rajpoot     . . . . . . 3 . . .
## Avesh Khan     . . . . . . 1 . 3 .
## B Kumar        . . . 9 . . 3 . 1 .

summary(getRatings(r0))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.000   3.000   3.000   3.423   3.000  21.000

evalRecomMethods(r0[1:dim(r0)[1]],k1=5,given=7,goodRating1=median(getRatings(r0)))

## Timing stopped at: 0.003 0 0.003

## Warning in .local(x, method, ...): 
##   Recommender 'UBCF Pearson' has failed and has been removed from the results!

a=eval(r0[1:dim(r0)[1]],0.8,k1=5,given1=7,goodRating1=median(getRatings(r0)),"UBCF")

## Recommender of type 'UBCF' for 'realRatingMatrix' 
## learned using 64 users.
## 16 x 195 rating matrix of class 'realRatingMatrix' with 1908 ratings.
##     RMSE      MSE      MAE 
## 2.672677 7.143203 1.956934

b=round(as(a,"matrix")[1:10,1:10])
c <- as(b,"realRatingMatrix")
v=as(c,"data.frame")
names(v) =c("bowler","batsman","WicketTaken")

17. Generate the Bowler Performance estmiate

The entire dataframe is regenerated with known and ‘predicted’ values

r1=merge(s,t,by=c("bowler","batsman"))
r2=merge(r1,u,by=c("bowler","batsman"))
r3=merge(r2,v,by=c("bowler","batsman"))
r4= select(r3,bowler, batsman, BallsBowled,RunsConceded,EconomyRate, WicketTaken)
head(r4)

##     bowler         batsman BallsBowled RunsConceded EconomyRate WicketTaken
## 1 A Mishra  AB de Villiers         102          144           8           4
## 2 A Mishra     Abdul Samad          13           20           7           4
## 3 A Mishra Abhishek Sharma          14           26           8           2
## 4 A Mishra      AD Russell          47           85           9           3
## 5 A Mishra        AJ Finch          45           61          11           4
## 6 A Mishra          AJ Tye          14           20           5           4

18. Conclusion

This post showed an approach for performing the Batsmen Performance Estimate & Bowler Performance Estimate. The performance of the recommender engine could have been better. In any case, I think this approach will work for player estimation provided the recommender algorithm is able to achieve a high degree of accuracy. This will be a good way to estimate as the algorithm will be able to determine features and nuances of batsmen and bowlers which cannot be captured by data.

References

Also see

To see all posts click Index of posts

IPL 2022: Near real-time analytics with GooglyPlusPlus!!!

It is that time of the year when there is “a song in the air, the lark’s on the wing, and the snail’s on the the thorn“. Yes, it is the that time of year when the grand gala event of IPL 2022 is underway. So, I managed to wake myself from my Covid-induced slumber, worked up my ‘creaking bones‘ and cranked up the GooglyPlusPlus machinery.

So now, every morning, a scheduled CRON tab entry will automatically download the previous night’s match data from Cricsheet, unzip, process and transform it into the necessary format required by my R package yorkr, and make it available to my Shiny app GooglyPlusPlus. Hence the data is current and you have access to ‘analytics-in-the-now’!.

As you know in 2021, I added a lot of new features to GooglyPlusPlus, new tabs to do even more. analytics – or in other words there is “more GooglyPlusPlus per click!!”. So now, you have the following

Batsman tab: For detailed analysis of batsmen
Bowler tab: For detailed analysis of bowlers
Match tab: Analysis of individual matches, plot of Runs vs SR, Wickets vs ER in power play, middle and death overs
Head-to-head tab: Detailed analysis of team-vs-team batting/bowling scorecard, batting, bowling performances, performances in power play, middle and death overs
Team performance tab: Analysis of team-vs-all other teams with batting /bowling scorecard, batting, bowling performances, performances in power play, middle and death overs
Optimisation tab: Allows one to pit batsmen vs bowlers and vice-versa. This tab also uses integer programming to optimise batting and bowling lineup
Batting analysis tab: Ranks batsmen using Runs or SR. Also plots performances of batsmen in power play, middle and death overs and plots them in a 4×4 grid
Bowling analysis tab: Ranks bowlers based on Wickets or ER. Also plots performances of bowlers in power play, middle and death overs and plots them in a 4×4 grid

Also note all these tabs and features are available for all T20 formats namely IPL, Intl. T20 (men, women), BBL, NTB, PSL, CPL, SSM.

Note: All charts are interactive, which means that you can hover, zoom-in, zoom-out, pan etc on the charts

The latest avatar of GooglyPlusPlus2022 is based on my R package yorkr with data from Cricsheet.

Go ahead, give GooglyPlusPlus a try!!!

To know all the new features and how to use them, check out these posts

Ranking of batsmen, bowlers – GooglyPlusPlus2021 interactively ranks T20 batsmen and bowlers!!!
Interactive charts – GooglyPlusPlus2021 is now fully interactive!!!
Detailed batsmen/bowler analytics – GooglyPlusPlus2021 enhanced with drill-down batsman, bowler analytics
Addition of Date Range picker to charts – GooglyPlusPlus2021 adds new bells and whistles!!
Analysis of power play, middle and death overs across players, teams – GooglyPlusPlus2021 now with power play, middle and death over analysis
Analysis based on 4 x 4 grid of players – GooglyPlusPlus2021: Towards more picturesque analytics!
Optimisation of batsmen/bowlers – GooglyPlusPlus2022 optimizes batting/bowling lineup

Here are some random analysis that can be done by GooglyPlusPlus across the tabs. Note the app will be updated daily and the analytics will be current throughout the season of IPL 2022

A) Match tab

a) GT vs DC – 2 Apr 2022

Runs vs SR – Gujarat Titans