Tag: convolutional neural network

Deconstructing Convolutional Neural Networks with Tensorflow and Keras

I have been very fascinated by how Convolution Neural  Networks have been able to, so efficiently,  do image classification and image recognition CNN’s have been very successful in in both these tasks. A good paper that explores the workings of a CNN Visualizing and Understanding Convolutional Networks  by Matthew D Zeiler and Rob Fergus. They show how through a reverse process of convolution using a deconvnet.

In their paper they show how by passing the feature map through a deconvnet ,which does the reverse process of the convnet, they can reconstruct what input pattern originally caused a given activation in the feature map

In the paper they say “A deconvnet can be thought of as a convnet model that uses the same components (filtering, pooling) but in reverse, so instead of mapping pixels to features, it does the opposite. An input image is presented to the CNN and features  activation computed throughout the layers. To examine a given convnet activation, we set all other activations in the layer to zero and pass the feature maps as input to the attached deconvnet layer. Then we successively (i) unpool, (ii) rectify and (iii) filter to reconstruct the activity in the layer beneath that gave rise to the chosen activation. This is then repeated until input pixel space is reached.”

I started to scout the internet to see how I can implement this reverse process of Convolution to understand what really happens under the hood of a CNN.  There are a lot of good articles and blogs, but I found this post Applied Deep Learning – Part 4: Convolutional Neural Networks take the visualization of the CNN one step further.

This post takes VGG16 as the pre-trained network and then uses this network to display the intermediate visualizations.  While this post was very informative and also the visualizations of the various images were very clear, I wanted to simplify the problem for my own understanding.

Hence I decided to take the MNIST digit classification as my base problem. I created a simple 3 layer CNN which gives close to 99.1% accuracy and decided to see if I could do the visualization.

As mentioned in the above post, there are 3 major visualisations

  1. Feature activations at the layer
  2. Visualisation of the filters
  3. Visualisation of the class outputs

Feature Activation – This visualization the feature activation at the 3 different layers for a given input image. It can be seen that first layer  activates based on the edge of the image. Deeper layers activate in a more abstract way.

Visualization of the filters: This visualization shows what patterns the filters respond maximally to. This is implemented in Keras here

To do this the following is repeated in a loop

  • Choose a loss function that maximizes the value of a convnet filter activation
  • Do gradient ascent (maximization) in input space that increases the filter activation

Visualizing Class Outputs of the MNIST Convnet: This process is similar to determining the filter activation. Here the convnet is made to generate an image that represents the category maximally.

You can access the Google colab notebook here – Deconstructing Convolutional Neural Networks in Tensoflow and Keras

import numpy as np
import pandas as pd
import os
import tensorflow as tf
import matplotlib.pyplot as plt
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D, Input
from keras.models import Model
from sklearn.model_selection import train_test_split
from keras.utils import np_utils
Using TensorFlow backend.
In [0]:
mnist=tf.keras.datasets.mnist
# Set training and test data and labels
(training_images,training_labels),(test_images,test_labels)=mnist.load_data()
In [0]:
#Normalize training data
X =np.array(training_images).reshape(training_images.shape[0],28,28,1) 
# Normalize the images by dividing by 255.0
X = X/255.0
X.shape
# Use one hot encoding for the labels
Y = np_utils.to_categorical(training_labels, 10)
Y.shape
# Split training data into training and validation data in the ratio of 80:20
X_train, X_validation, y_train, y_validation = train_test_split(X,Y,test_size=0.20, random_state=42)
In [4]:
# Normalize test data
X_test =np.array(test_images).reshape(test_images.shape[0],28,28,1) 
X_test=X_test/255.0
#Use OHE for the test labels
Y_test = np_utils.to_categorical(test_labels, 10)
X_test.shape
Out[4]:
(10000, 28, 28, 1)

Display data

Display the training data and the corresponding labels

In [5]:
print(training_labels[0:10])
f, axes = plt.subplots(1, 10, sharey=True,figsize=(10,10))
for i,ax in enumerate(axes.flat):
    ax.axis('off')
    ax.imshow(X[i,:,:,0],cmap="gray")

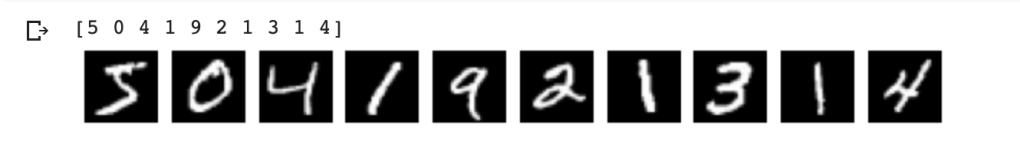
Create a Convolutional Neural Network

The CNN consists of 3 layers

  • Conv2D of size 28 x 28 with 24 filters
  • Perform Max pooling
  • Conv2D of size 14 x 14 with 48 filters
  • Perform max pooling
  • Conv2d of size 7 x 7 with 64 filters
  • Flatten
  • Use Dense layer with 128 units
  • Perform 25% dropout
  • Perform categorical cross entropy with softmax activation function
In [0]:
num_classes=10
inputs = Input(shape=(28,28,1))
x = Conv2D(24,kernel_size=(3,3),padding='same',activation="relu")(inputs)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(48, (3, 3), padding='same',activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(64, (3, 3), padding='same',activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Flatten()(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.25)(x)
output = Dense(num_classes,activation="softmax")(x)

model = Model(inputs,output)

model.compile(loss='categorical_crossentropy', 
          optimizer='adam', 
          metrics=['accuracy'])

Summary of CNN

Display the summary of CNN

In [7]:
model.summary()
Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 28, 28, 24)        240       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 14, 14, 24)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 14, 14, 48)        10416     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 7, 7, 48)          0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 7, 7, 64)          27712     
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 3, 3, 64)          0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 576)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 128)               73856     
_________________________________________________________________
dropout_1 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 10)                1290      
=================================================================
Total params: 113,514
Trainable params: 113,514
Non-trainable params: 0
_________________________________________________________________

Perform Gradient descent and validate with the validation data

In [8]:
epochs = 20
batch_size=256
history = model.fit(X_train,y_train,
         epochs=epochs,
         batch_size=batch_size,
         validation_data=(X_validation,y_validation))
————————————————
acc = history.history[ ‘accuracy’ ]
val_acc = history.history[ ‘val_accuracy’ ]
loss = history.history[ ‘loss’ ]
val_loss = history.history[‘val_loss’ ]
epochs = range(len(acc)) # Get number of epochs
#————————————————
# Plot training and validation accuracy per epoch
#————————————————
plt.plot ( epochs, acc,label=”training accuracy” )
plt.plot ( epochs, val_acc, label=’validation acuracy’ )
plt.title (‘Training and validation accuracy’)
plt.legend()
plt.figure()
#————————————————
# Plot training and validation loss per epoch
#————————————————
plt.plot ( epochs, loss , label=”training loss”)
plt.plot ( epochs, val_loss,label=”validation loss” )
plt.title (‘Training and validation loss’ )
plt.legend()
Test model on test data
f, axes = plt.subplots(1, 10, sharey=True,figsize=(10,10))
for i,ax in enumerate(axes.flat):
ax.axis(‘off’)
ax.imshow(X_test[i,:,:,0],cmap=”gray”)
l=[]
for i in range(10):
  x=X_test[i].reshape(1,28,28,1)
  y=model.predict(x)
  m = np.argmax(y, axis=1)
  print(m)

[7]
[2]
[1]
[0]
[4]
[1]
[4]
[9]
[5]
[9]

Generate the filter activations at the intermediate CNN layers

In [12]:
img = test_images[51].reshape(1,28,28,1)
fig = plt.figure(figsize=(5,5))
print(img.shape)
plt.imshow(img[0,:,:,0],cmap="gray")
plt.axis('off')

Display the activations at the intermediate layers

This displays the intermediate activations as the image passes through the filters and generates these feature maps

In [13]:
layer_names = ['conv2d_4', 'conv2d_5', 'conv2d_6']

layer_outputs = [layer.output for layer in model.layers if 'conv2d' in layer.name]
activation_model = Model(inputs=model.input,outputs=layer_outputs)
intermediate_activations = activation_model.predict(img)
images_per_row = 8
max_images = 8

for layer_name, layer_activation in zip(layer_names, intermediate_activations):
    print(layer_name,layer_activation.shape)
    n_features = layer_activation.shape[-1]
    print("features=",n_features)
    n_features = min(n_features, max_images)
    print(n_features)

    size = layer_activation.shape[1]
    print("size=",size)
    n_cols = n_features // images_per_row
    display_grid = np.zeros((size * n_cols, images_per_row * size))


    for col in range(n_cols):
      for row in range(images_per_row):
          channel_image = layer_activation[0,:, :, col * images_per_row + row]

          channel_image -= channel_image.mean()
          channel_image /= channel_image.std()
          channel_image *= 64
          channel_image += 128
          channel_image = np.clip(channel_image, 0, 255).astype('uint8')
          display_grid[col * size : (col + 1) * size,
                         row * size : (row + 1) * size] = channel_image
    scale = 2. / size
    plt.figure(figsize=(scale * display_grid.shape[1],
                        scale * display_grid.shape[0]))
    plt.axis('off')
    plt.title(layer_name)
    plt.grid(False)
    plt.imshow(display_grid, aspect='auto', cmap='viridis')
    
plt.show()

It can be seen that at the higher layers only abstract features of the input image are captured

# To fix the ImportError: cannot import name 'imresize' in the next cell. Run this cell. Then comment and restart and run all
#!pip install scipy==1.1.0

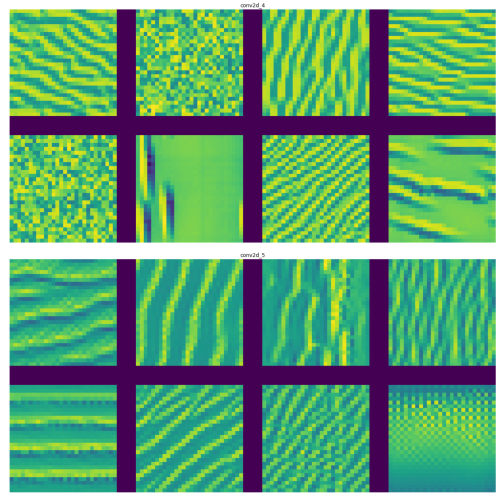
Visualize the pattern that the filters respond to maximally

  • Choose a loss function that maximizes the value of the CNN filter in a given layer
  • Start from a blank input image.
  • Do gradient ascent in input space. Modify input values so that the filter activates more
  • Repeat this in a loop.
In [14]:
from vis.visualization import visualize_activation, get_num_filters
from vis.utils import utils
from vis.input_modifiers import Jitter

max_filters = 24
selected_indices = []
vis_images = [[], [], [], [], []]
i = 0
selected_filters = [[0, 3, 11, 15, 16, 17, 18, 22], 
    [8, 21, 23, 25, 31, 32, 35, 41], 
    [2, 7, 11, 14, 19, 26, 35, 48]]

# Set the layers
layer_name = ['conv2d_4', 'conv2d_5', 'conv2d_6']
# Set the layer indices
layer_idx = [1,3,5]
for layer_name,layer_idx in zip(layer_name,layer_idx):


    # Visualize all filters in this layer.
    if selected_filters:
        filters = selected_filters[i]
    else:
        # Randomly select filters
        filters = sorted(np.random.permutation(get_num_filters(model.layers[layer_idx]))[:max_filters])
    selected_indices.append(filters)

    # Generate input image for each filter.
    # Loop through the selected filters in each layer and generate the activation of these filters
    for idx in filters:
        img = visualize_activation(model, layer_idx, filter_indices=idx, tv_weight=0., 
                                   input_modifiers=[Jitter(0.05)], max_iter=300) 
        vis_images[i].append(img)

    # Generate stitched image palette with 4 cols so we get 2 rows.
    stitched = utils.stitch_images(vis_images[i], cols=4)    
    plt.figure(figsize=(20, 30))
    plt.title(layer_name)
    plt.axis('off')
    stitched = stitched.reshape(1,61,127,1)
    plt.imshow(stitched[0,:,:,0])
    plt.show()
    i += 1
from vis.utils import utils
new_vis_images = [[], [], [], [], []]
i = 0
layer_name = ['conv2d_4', 'conv2d_5', 'conv2d_6']
layer_idx = [1,3,5]
for layer_name,layer_idx in zip(layer_name,layer_idx):
   
    # Generate input image for each filter.
    for j, idx in enumerate(selected_indices[i]):
        img = visualize_activation(model, layer_idx, filter_indices=idx, 
                                   seed_input=vis_images[i][j], input_modifiers=[Jitter(0.05)], max_iter=300) 
        #img = utils.draw_text(img, 'Filter {}'.format(idx))  
        new_vis_images[i].append(img)

    stitched = utils.stitch_images(new_vis_images[i], cols=4)   
    plt.figure(figsize=(20, 30))
    plt.title(layer_name)
    plt.axis('off')
    print(stitched.shape)
    stitched = stitched.reshape(1,61,127,1)
    plt.imshow(stitched[0,:,:,0])
    plt.show()
    i += 1

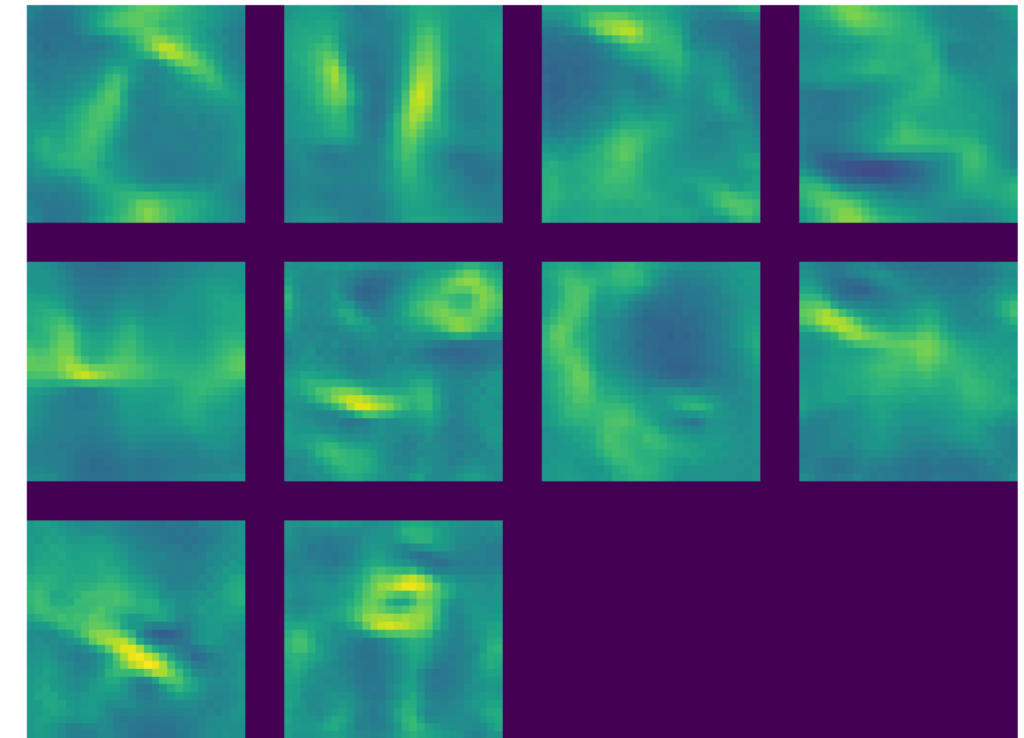
Visualizing Class Outputs

Here the CNN will generate the image that maximally represents the category. Each of the output represents one of the digits as can be seen below

In [16]:
from vis.utils import utils
from keras import activations
codes = '''
zero 0
one 1
two 2
three 3
four 4
five 5
six 6
seven 7
eight 8
nine 9
'''
layer_idx=10
initial = []
images = []
tuples = []
# Swap softmax with linear for better visualization
model.layers[layer_idx].activation = activations.linear
model = utils.apply_modifications(model)
for line in codes.split('\n'):
    if not line:
        continue
    name, idx = line.rsplit(' ', 1)
    idx = int(idx)
    img = visualize_activation(model, layer_idx, filter_indices=idx, 
                               tv_weight=0., max_iter=300, input_modifiers=[Jitter(0.05)])

    initial.append(img)
    tuples.append((name, idx))

i = 0
for name, idx in tuples:
    img = visualize_activation(model, layer_idx, filter_indices=idx,
                               seed_input = initial[i], max_iter=300, input_modifiers=[Jitter(0.05)])
    #img = utils.draw_text(img, name) # Unable to display text on gray scale image
    i += 1
    images.append(img)

stitched = utils.stitch_images(images, cols=4)
plt.figure(figsize=(20, 20))
plt.axis('off')
stitched = stitched.reshape(1,94,127,1)
plt.imshow(stitched[0,:,:,0])

plt.show()

In the grid below the class outputs show the MNIST digits to which output responds to maximally. We can see the ghostly outline
of digits 0 – 9. We can clearly see the outline if 0,1, 2,3,4,5 (yes, it is there!),6,7, 8 and 9. If you look at this from a little distance the digits are clearly visible. Isn’t that really cool!!


 

Conclusion:


It is really interesting to see the class outputs which show the image to which the class output responds to maximally. In the
post Applied Deep Learning – Part 4: Convolutional Neural Networks the class output show much more complicated images and is worth a look. It is really interesting to note that the model has adjusted the filter values and the weights of the fully connected network to maximally respond to the MNIST digits

References

1. Visualizing and Understanding Convolutional Networks
2. Applied Deep Learning – Part 4: Convolutional Neural Networks
3. Visualizing Intermediate Activations of a CNN trained on the MNIST Dataset
4. How convolutional neural networks see the world
5. Keras – Activation_maximization

Also see

1. Using Reinforcement Learning to solve Gridworld
2. Deep Learning from first principles in Python, R and Octave – Part 8
3. Cricketr learns new tricks : Performs fine-grained analysis of players
4. Video presentation on Machine Learning, Data Science, NLP and Big Data – Part 1
5. Big Data-2: Move into the big league:Graduate from R to SparkR
6. OpenCV: Fun with filters and convolution
7. Powershell GUI – Adding bells and whistles

To see all posts click Index of posts

Understanding Neural Style Transfer with Tensorflow and Keras

Neural Style Transfer (NST)  is a fascinating area of Deep Learning and Convolutional Neural Networks. NST is an interesting technique, in which the style from an image, known as the ‘style image’ is transferred to another image ‘content image’ and we get a third a image which is a generated image which has the content of the original image and the style of another image.

NST can be used to reimagine how famous painters like Van Gogh, Claude Monet or a Picasso would have visualised a scenery or architecture. NST uses Convolutional Neural Networks (CNNs) to achieve this artistic style transfer from one image to another. NST was originally implemented by Gati et al., in their paper Neural Algorithm of Artistic Style. Convolutional Neural Networks have been very successful in image classification image recognition et cetera. CNN networks have also been have also generated very interesting pictures using Neural Style Transfer which will be shown in this post. An interesting aspect of CNN’s is that the first couple of layers in the CNN capture basic features of the image like edges and  pixel values. But as we go deeper into the CNN, the network captures higher level features of the input image.

To get started with Neural Style transfer  we will be using the VGG19 pre-trained network. The VGG19 CNN is a compact pre-trained your network which can be used for performing the NST. However, we could have also used Resnet or InceptionV3 networks for this purpose but these are very large networks. The idea of using a network trained on a different task and applying it to a new task is called transfer learning.

What needs to be done to transfer the style from one of the image to another image. This brings us to the question – What is ‘style’? What is it that distinguishes Van Gogh’s painting or Picasso’s cubist art. Convolutional Neural Networks capture basic features in the lower layers and much more complex features in the deeper layers.  Style can be computed by taking the correlation of the feature maps in a layer L. This is my interpretation of how style is captured.  Since style  is intrinsic to  the image, it  implies that the style feature would exist across all the filters in a layer. Hence, to pick up this style we would need to get the correlation of the filters across channels of a lawyer. This is computed mathematically, using the Gram matrix which calculates the correlation of the activation of a the filter by the style image and generated image

To transfer the style from one image to the content image we need to do two parallel operations while doing forward propagation
– Compute the content loss between the source image and the generated image
– Compute the style loss between the style image and the generated image
– Finally we need to compute the total loss

In order to get transfer the style from the ‘style’ image to the ‘content ‘image resulting in a  ‘generated’  image  the total loss has to be minimised. Therefore backward propagation with gradient descent  is done to minimise the total loss comprising of the content and style loss.

Initially we make the Generated Image ‘G’ the same as the source image ‘S’

The content loss at layer ‘l’

L_{content} = 1/2 \sum_{i}^{j} ( F^{l}_{i,j} - P^{l}_{i,j})^{2}

where F^{l}_{i,j} and P^{l}_{i,j} represent the activations at layer ‘l’ in a filter i, at position ‘j’. The intuition is that the activations will be same for similar source and generated image. We need to minimise the content loss so that the generated stylized image is as close to the original image as possible. An intermediate layer of VGG19 block5_conv2 is used

The Style layers that are are used are

style_layers = [‘block1_conv1’,
‘block2_conv1’,
‘block3_conv1’,
‘block4_conv1’,
‘block5_conv1’]
To compute the Style Loss the Gram matrix needs to be computed. The Gram Matrix is computed by unrolling the filters as shown below (source: Convolutional Neural Networks by Prof Andrew Ng, Coursera). The result is a matrix of size n_{c} x n_{c} where n_{c} is the number of channels
The above diagram shows the filters of height n_{H} and width n_{W} with n_{C} channels
The contribution of layer ‘l’ to style loss is given by
L^{'}_{style} = \frac{\sum_{i}^{j} (G^{2}_{i,j} - A^l{i,j})^2}{4N^{2}_{l}M^{2}_{l}}
where G_{i,j}  and A_{i,j} are the Gram matrices of the style and generated images respectively. By minimising the distance in the gram matrices of the style and generated image we can ensure that generated image is a stylized version of the original image similar to the style image
The total loss is given by
L_{total} = \alpha L_{content} + \beta L_{style}
Back propagation with gradient descent works to minimise the content loss between the source and generated image, while the style loss tries to minimise the discrepancies in the style of the style image and generated image. Running through forward and backpropagation through several epochs successfully transfers the style from the style image to the source image.
You can check the Notebook at Neural Style Transfer

Note: The code in this notebook is largely based on the Neural Style Transfer tutorial from Tensorflow, though I may have taken some changes from other blogs. I also made a few changes to the code in this tutorial, like removing the scaling factor, or the class definition (Personally, I belong to the old school (C language) and am not much in love with the ‘self.”..All references are included below

Note: Here is a interesting thought. Could we do a Neural Style Transfer in music? Imagine Carlos Santana playing ‘Hotel California’ or Brian May style in ‘Another brick in the wall’. While our first reaction would be that it may not sound good as we are used to style of these songs, we may be surprised by a possible style transfer. This is definitely music to the ears!

 

Here are few runs from this

A) Run 1

1. Neural Style Transfer – a) Content Image – My portrait.  b) Style Image – Wassily Kadinsky Oil on canvas, 1913, Vassily Kadinsky’s composition

 

2. Result of Neural Style Transfer

 

 

2) Run 2

a) Content Image – Portrait of my parents b) Style Image –  Vincent Van Gogh’s ,Starry Night Oil on canvas 1889

 

2. Result of Neural Style Transfer

 

 

Run 3

1.  Content Image – Caesar 2 (Masai Mara- 20 Jun 2018).  Style Image – The Great Wave at Kanagawa – Katsushika Hokosai, 1826-1833

 

Screenshot 2020-04-12 at 12.40.44 PM

2. Result of Neural Style Transfer

lkg

 

 

Run 4

1.   Content Image – Junagarh Fort , Rajasthan   Sep 2016              b) Style Image – Le Pont Japonais by Claude Monet, Oil on canvas, 1920

 

 

2. Result of Neural Style Transfer

 

Neural Style Transfer is a very ingenious idea which shows that we can segregate the style of a painting and transfer to another image.

References

1. A Neural Algorithm of Artistic Style, Leon A. Gatys, Alexander S. Ecker, Matthias Bethge
2. Neural style transfer
3. Neural Style Transfer: Creating Art with Deep Learning using tf.keras and eager execution
4. Convolutional Neural Network, DeepLearning.AI Specialization, Prof Andrew Ng
5. Intuitive Guide to Neural Style Transfer

See also

1. Big Data-5: kNiFi-ing through cricket data with yorkpy
2. Cricketr adds team analytics to its repertoire
3. Cricpy performs granular analysis of players
4. My book ‘Deep Learning from first principles:Second Edition’ now on Amazon
5. Programming Zen and now – Some essential tips-2
6. The Anomaly
7. Practical Machine Learning with R and Python – Part 5
8. Literacy in India – A deepR dive
9. “Is it an animal? Is it an insect?” in Android

To see all posts click Index of posts