“Once upon a time, I, Chuang Tzu, dreamt I was a butterfly, fluttering hither and thither, to all intents and purposes a butterfly. I was conscious only of following my fancies as a butterfly, and was unconscious of my individuality as a man. Suddenly, I awoke, and there I lay, myself again. Now I do not know whether I was then a man dreaming I was a butterfly, or whether I am now a butterfly dreaming that I am a man.”
from The Brain: The Story of you – David Eagleman
“Thought is a great big vector of neural activity”
Prof Geoffrey Hinton
Introduction
This is the third part in my series on Deep Learning from first principles in Python, R and Octave. In the first part Deep Learning from first principles in Python, R and Octave-Part 1, I implemented logistic regression as a 2 layer neural network. The 2nd part Deep Learning from first principles in Python, R and Octave-Part 2, dealt with the implementation of 3 layer Neural Networks with 1 hidden layer to perform classification tasks, where the 2 classes cannot be separated by a linear boundary. In this third part, I implement a multi-layer, Deep Learning (DL) network of arbitrary depth (any number of hidden layers) and arbitrary height (any number of activation units in each hidden layer). The implementations of these Deep Learning networks, in all the 3 parts, are based on vectorized versions in Python, R and Octave. The implementation in the 3rd part is for a L-layer Deep Netwwork, but without any regularization, early stopping, momentum or learning rate adaptation techniques. However even the barebones multi-layer DL, is a handful and has enough hyperparameters to fine-tune and adjust.
 Checkout my book ‘Deep Learning from first principles: Second Edition – In vectorized Python, R and Octave’. My book starts with the implementation of a simple 2-layer Neural Network and works its way to a generic L-Layer Deep Learning Network, with all the bells and whistles. The derivations have been discussed in detail. The code has been extensively commented and included in its entirety in the Appendix sections. My book is available on Amazon as paperback ($18.99) and in kindle version($9.99/Rs449).
Checkout my book ‘Deep Learning from first principles: Second Edition – In vectorized Python, R and Octave’. My book starts with the implementation of a simple 2-layer Neural Network and works its way to a generic L-Layer Deep Learning Network, with all the bells and whistles. The derivations have been discussed in detail. The code has been extensively commented and included in its entirety in the Appendix sections. My book is available on Amazon as paperback ($18.99) and in kindle version($9.99/Rs449).
You can download the PDF version of this book from Github at https://github.com/tvganesh/DeepLearningBook-2ndEd
The implementation of the vectorized L-layer Deep Learning network in Python, R and Octave were both exhausting, and exacting!! Keeping track of the indices, layer number and matrix dimensions required quite bit of focus. While the implementation was demanding, it was also very exciting to get the code to work. The trick was to be able to shift gears between the slight quirkiness between the languages. Here are some of challenges I faced.
1. Python and Octave allow multiple return values to be unpacked in a single statement. With R, unpacking multiple return values from a list, requires the list returned, to be unpacked separately. I did see that there is a package gsubfn, which does this. I hope this feature becomes a base R feature.
2. Python and R allow dissimilar elements to be saved and returned from functions using dictionaries or lists respectively. However there is no real equivalent in Octave. The closest I got to this functionality in Octave, was the ‘cell array’. But the cell array can be accessed only by the index, and not with the key as in a Python dictionary or R list. This makes things just a bit more difficult in Octave.
3. Python and Octave include implicit broadcasting. In R, broadcasting is not implicit, but R has a nifty function, the sweep(), with which we can broadcast either by columns or by rows
4. The closest equivalent of Python’s dictionary, or R’s list, in Octave is the cell array. However I had to manage separate cell arrays for weights and biases and during gradient descent and separate gradients dW and dB
5. In Python the rank-1 numpy arrays can be annoying at times. This issue is not present in R and Octave.
Though the number of lines of code for Deep Learning functions in Python, R and Octave are about ~350 apiece, they have been some of the most difficult code I have implemented. The current vectorized implementation supports the relu, sigmoid and tanh activation functions as of now. I will be adding other activation functions like the ‘leaky relu’, ‘softmax’ and others, to the implementation in the weeks to come.
While testing with different hyper-parameters namely i) the number of hidden layers, ii) the number of activation units in each layer, iii) the activation function and iv) the number iterations, I found the L-layer Deep Learning Network to be very sensitive to these hyper-parameters. It is not easy to tune the parameters. Adding more hidden layers, or more units per layer, does not help and mostly results in gradient descent getting stuck in some local minima. It does take a fair amount of trial and error and very close observation on how the DL network performs for logical changes. We then can zero in on the most the optimal solution. Feel free to download/fork my code from Github DeepLearning-Part 3 and play around with the hyper-parameters for your own problems.
Derivation of a Multi Layer Deep Learning Network
Note: A detailed discussion of the derivation below is available in my video presentation Neural Network 4
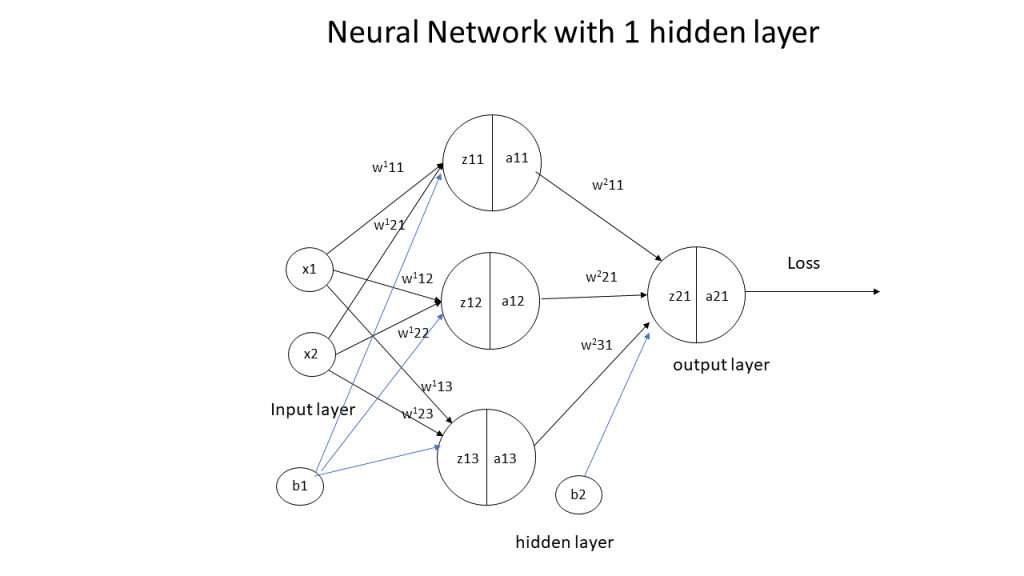
Lets take a simple 3 layer Neural network with 3 hidden layers and an output layer

In the forward propagation cycle the equations are
and
and
and
The loss function is given by
and
For a binary classification the output activation function is the sigmoid function given by
. It can be shown that
see equation 2 in Part 1
see equation (f) in Part 1
and since
because
-(1a)
and -(1b)
-(1c)
since
and
-(1d)
because
Also
– (2a)
– (2b)
– (2c)
– (2d)
Inspecting the above equations (1a – 1d & 2a-2d), our ‘Uber deep, bottomless’ brain can easily discern the pattern in these equations. The equation for any layer ‘l’ is of the form
and
The equation for the backward propagation have the general form
Some other important results The derivatives of the activation functions in the implemented Deep Learning network
g(z) = sigmoid(z) = = a g’(z) = a(1-a) – See Part 1
g(z) = tanh(z) = a g’(z) =
g(z) = relu(z) = z when z>0 and 0 when z 0 and 0 when z <= 0
While it appears that there is a discontinuity for the derivative at 0 the small value at the discontinuity does not present a problem
The implementation of the multi layer vectorized Deep Learning Network for Python, R and Octave is included below. For all these implementations, initially I create the size and configuration of the the Deep Learning network with the layer dimennsions So for example layersDimension Vector ‘V’ of length L indicating ‘L’ layers where
V (in Python)= , …
V (in R)= , …
V (in Octave)= [ …
In all of these implementations the first element is the number of input features to the Deep Learning network and the last element is always a ‘sigmoid’ activation function since all the problems deal with binary classification.
The number of elements between the first and the last element are the number of hidden layers and the magnitude of each is the number of activation units in each hidden layer, which is specified while actually executing the Deep Learning network using the function L_Layer_DeepModel(), in all the implementations Python, R and Octave
1a. Classification with Multi layer Deep Learning Network – Relu activation(Python)
In the code below a 4 layer Neural Network is trained to generate a non-linear boundary between the classes. In the code below the ‘Relu’ Activation function is used. The number of activation units in each layer is 9. The cost vs iterations is plotted in addition to the decision boundary. Further the accuracy, precision, recall and F1 score are also computed
import os import numpy as np import matplotlib.pyplot as plt import matplotlib.colors import sklearn.linear_model from sklearn.model_selection import train_test_split from sklearn.datasets import make_classification, make_blobs from matplotlib.colors import ListedColormap import sklearn import sklearn.datasets #from DLfunctions import plot_decision_boundary execfile("./DLfunctions34.py") # os.chdir("C:\\software\\DeepLearning-Posts\\part3") # Create clusters of 2 classes X1, Y1 = make_blobs(n_samples = 400, n_features = 2, centers = 9, cluster_std = 1.3, random_state = 4) #Create 2 classes Y1=Y1.reshape(400,1) Y1 = Y1 % 2 X2=X1.T Y2=Y1.T # Set the dimensions of DL Network # Below we have # 2 - 2 input features # 9,9 - 2 hidden layers with 9 activation units per layer and # 1 - 1 sigmoid activation unit in the output layer as this is a binary classification # The activation in the hidden layer is the 'relu' specified in L_Layer_DeepModel layersDimensions = [2, 9, 9,1] # 4-layer model parameters = L_Layer_DeepModel(X2, Y2, layersDimensions,hiddenActivationFunc='relu', learning_rate = 0.3,num_iterations = 2500, fig="fig1.png") #Plot the decision boundary plot_decision_boundary(lambda x: predict(parameters, x.T), X2,Y2,str(0.3),"fig2.png") # Compute the confusion matrix yhat = predict(parameters,X2) from sklearn.metrics import confusion_matrix a=confusion_matrix(Y2.T,yhat.T) from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score print('Accuracy: {:.2f}'.format(accuracy_score(Y2.T, yhat.T))) print('Precision: {:.2f}'.format(precision_score(Y2.T, yhat.T))) print('Recall: {:.2f}'.format(recall_score(Y2.T, yhat.T))) print('F1: {:.2f}'.format(f1_score(Y2.T, yhat.T)))## Accuracy: 0.90 ## Precision: 0.91 ## Recall: 0.87 ## F1: 0.89


For more details on metrics like Accuracy, Recall, Precision etc. used in classification take a look at my post Practical Machine Learning with R and Python – Part 2. More details about these and other metrics besides implementation of the most common machine learning algorithms are available in my book My book ‘Practical Machine Learning with R and Python’ on Amazon
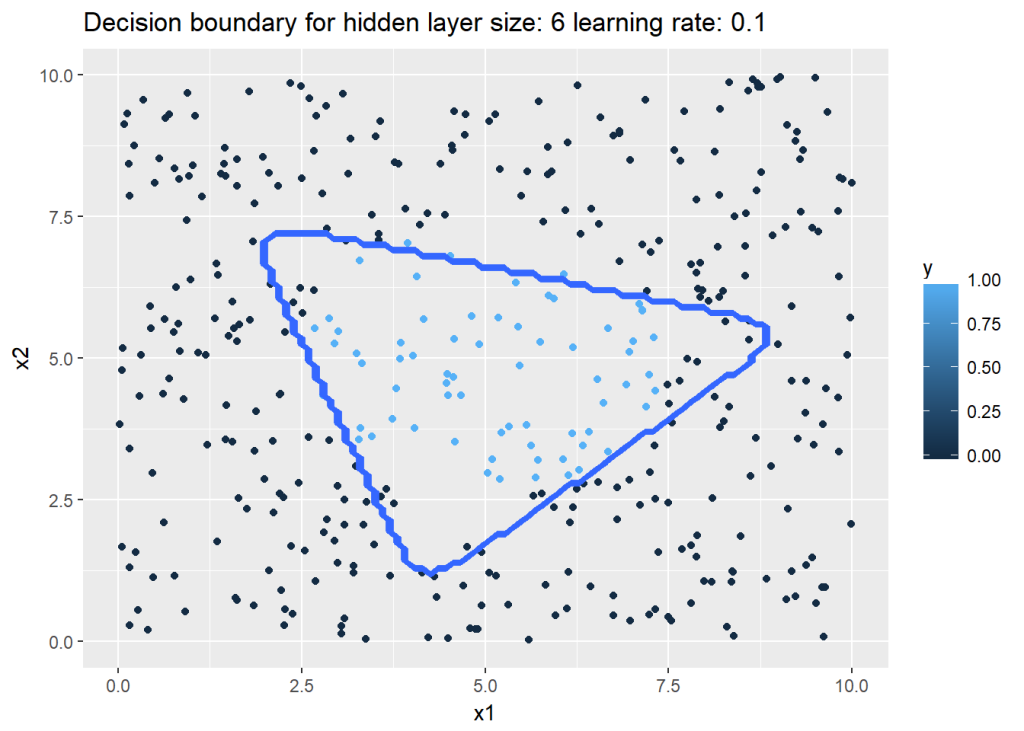
1b. Classification with Multi layer Deep Learning Network – Relu activation(R)
In the code below, binary classification is performed on the same data set as above using the Relu activation function. The DL network is same as above
library(ggplot2)
# Read the data
z <- as.matrix(read.csv("data.csv",header=FALSE))
x <- z[,1:2]
y <- z[,3]
X1 <- t(x)
Y1 <- t(y)
# Set the dimensions of the Deep Learning network
# No of input features =2, 2 hidden layers with 9 activation units and 1 output layer
layersDimensions = c(2, 9, 9,1)
# Execute the Deep Learning Neural Network
retvals = L_Layer_DeepModel(X1, Y1, layersDimensions,
hiddenActivationFunc='relu',
learningRate = 0.3,
numIterations = 5000,
print_cost = True)library(ggplot2)
source("DLfunctions33.R")
# Get the computed costs
costs <- retvals[['costs']]
# Create a sequence of iterations
numIterations=5000
iterations <- seq(0,numIterations,by=1000)
df <-data.frame(iterations,costs)
# Plot the Costs vs number of iterations
ggplot(df,aes(x=iterations,y=costs)) + geom_point() +geom_line(color="blue") +
xlab('No of iterations') + ylab('Cost') + ggtitle("Cost vs No of iterations")
# Plot the decision boundary
plotDecisionBoundary(z,retvals,hiddenActivationFunc="relu",0.3)
library(caret)
# Predict the output for the data values
yhat <-predict(retvals$parameters,X1,hiddenActivationFunc="relu")
yhat[yhat==FALSE]=0
yhat[yhat==TRUE]=1
# Compute the confusion matrix
confusionMatrix(yhat,Y1)## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 201 10
## 1 21 168
##
## Accuracy : 0.9225
## 95% CI : (0.8918, 0.9467)
## No Information Rate : 0.555
## P-Value [Acc > NIR] : < 2e-16
##
## Kappa : 0.8441
## Mcnemar's Test P-Value : 0.07249
##
## Sensitivity : 0.9054
## Specificity : 0.9438
## Pos Pred Value : 0.9526
## Neg Pred Value : 0.8889
## Prevalence : 0.5550
## Detection Rate : 0.5025
## Detection Prevalence : 0.5275
## Balanced Accuracy : 0.9246
##
## 'Positive' Class : 0
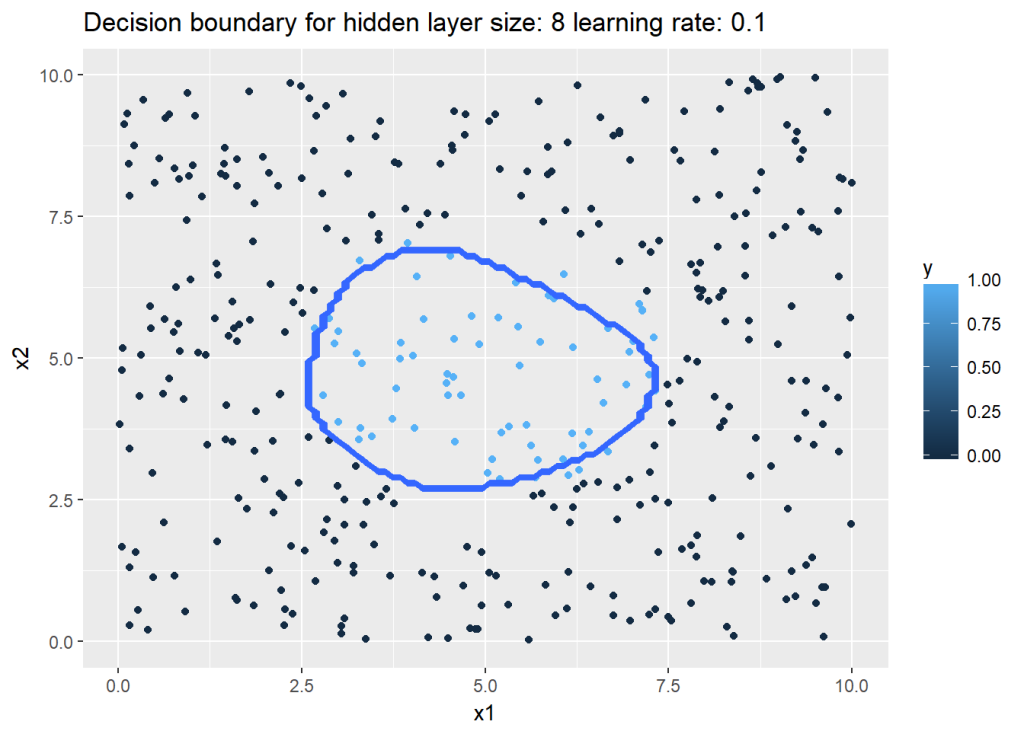
## 1c. Classification with Multi layer Deep Learning Network – Relu activation(Octave)
Included below is the code for performing classification. Incidentally Octave does not seem to have implemented the confusion matrix, but confusionmat is available in Matlab.
# Read the data
data=csvread("data.csv");
X=data(:,1:2);
Y=data(:,3);
# Set layer dimensions
layersDimensions = [2 9 7 1] #tanh=-0.5(ok), #relu=0.1 best!
# Execute Deep Network
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='relu',
learningRate = 0.1,
numIterations = 10000);
plotCostVsIterations(10000,costs);
plotDecisionBoundary(data,weights, biases,hiddenActivationFunc="tanh")


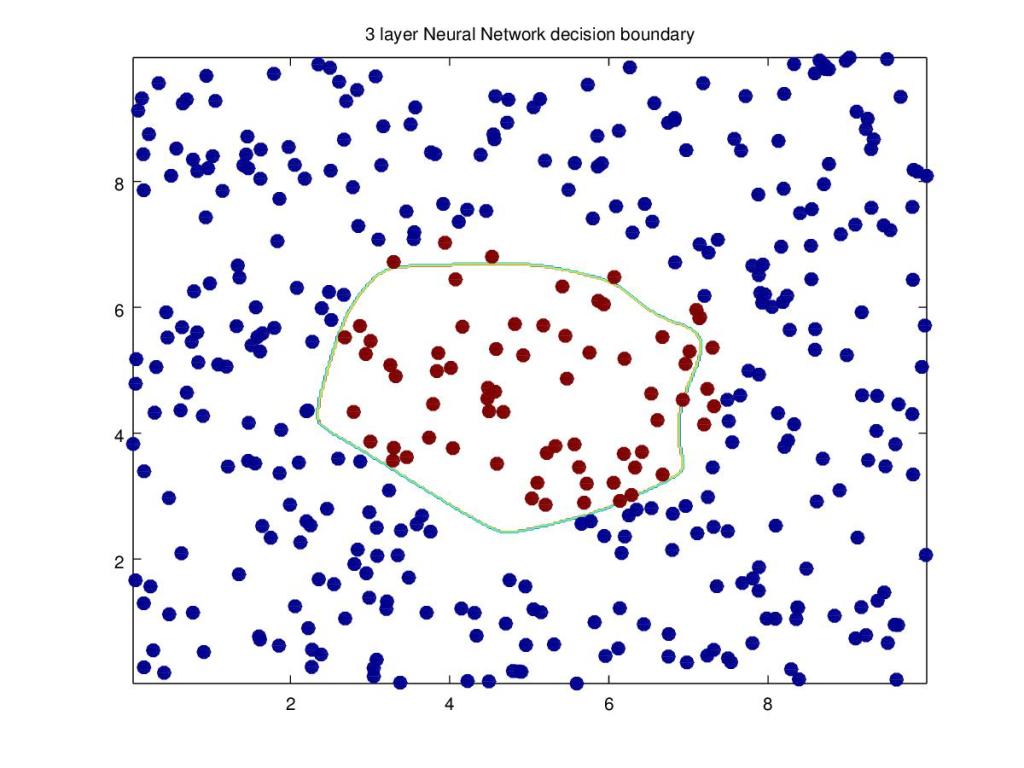
2a. Classification with Multi layer Deep Learning Network – Tanh activation(Python)
Below the Tanh activation function is used to perform the same classification. I found the Tanh activation required a simpler Neural Network of 3 layers.
# Tanh activation
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors
import sklearn.linear_model
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification, make_blobs
from matplotlib.colors import ListedColormap
import sklearn
import sklearn.datasets
#from DLfunctions import plot_decision_boundary
os.chdir("C:\\software\\DeepLearning-Posts\\part3")
execfile("./DLfunctions34.py")
# Create the dataset
X1, Y1 = make_blobs(n_samples = 400, n_features = 2, centers = 9,
cluster_std = 1.3, random_state = 4)
#Create 2 classes
Y1=Y1.reshape(400,1)
Y1 = Y1 % 2
X2=X1.T
Y2=Y1.T
# Set the dimensions of the Neural Network
layersDimensions = [2, 4, 1] # 3-layer model
# Compute the DL network
parameters = L_Layer_DeepModel(X2, Y2, layersDimensions, hiddenActivationFunc='tanh', learning_rate = .5,num_iterations = 2500,fig="fig3.png")
#Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X2,Y2,str(0.5),"fig4.png")
2b. Classification with Multi layer Deep Learning Network – Tanh activation(R)
R performs better with a Tanh activation than the Relu as can be seen below
#Set the dimensions of the Neural Network
layersDimensions = c(2, 9, 9,1)
library(ggplot2)
# Read the data
z <- as.matrix(read.csv("data.csv",header=FALSE))
x <- z[,1:2]
y <- z[,3]
X1 <- t(x)
Y1 <- t(y)
# Execute the Deep Model
retvals = L_Layer_DeepModel(X1, Y1, layersDimensions,
hiddenActivationFunc='tanh',
learningRate = 0.3,
numIterations = 5000,
print_cost = True)# Get the costs
costs <- retvals[['costs']]
iterations <- seq(0,numIterations,by=1000)
df <-data.frame(iterations,costs)
# Plot Cost vs number of iterations
ggplot(df,aes(x=iterations,y=costs)) + geom_point() +geom_line(color="blue") +
xlab('No of iterations') + ylab('Cost') + ggtitle("Cost vs No of iterations")
#Plot the decision boundary
plotDecisionBoundary(z,retvals,hiddenActivationFunc="tanh",0.3)
2c. Classification with Multi layer Deep Learning Network – Tanh activation(Octave)
The code below uses the Tanh activation in the hidden layers for Octave
# Read the data
data=csvread("data.csv");
X=data(:,1:2);
Y=data(:,3);
# Set layer dimensions
layersDimensions = [2 9 7 1] #tanh=-0.5(ok), #relu=0.1 best!
# Execute Deep Network
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='tanh',
learningRate = 0.1,
numIterations = 10000);
plotCostVsIterations(10000,costs);
plotDecisionBoundary(data,weights, biases,hiddenActivationFunc="tanh")


3. Bernoulli’s Lemniscate
To make things more interesting, I create a 2D figure of the Bernoulli’s lemniscate to perform non-linear classification. The Lemniscate is given by the equation
=

3a. Classifying a lemniscate with Deep Learning Network – Relu activation(Python)
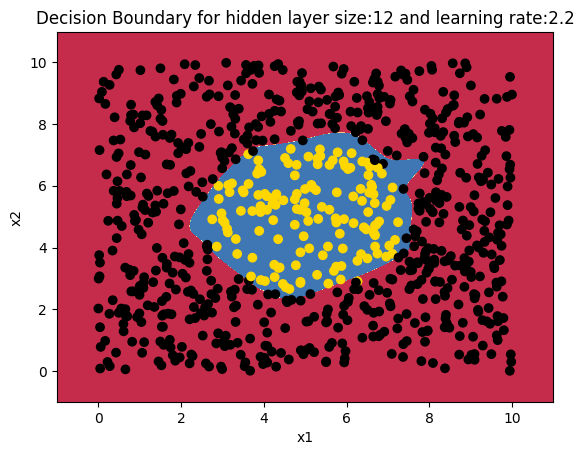
import os import numpy as np import matplotlib.pyplot as plt os.chdir("C:\\software\\DeepLearning-Posts\\part3") execfile("./DLfunctions33.py") x1=np.random.uniform(0,10,2000).reshape(2000,1) x2=np.random.uniform(0,10,2000).reshape(2000,1) X=np.append(x1,x2,axis=1) X.shape # Create a subset of values where squared is <0,4. Perform ravel() to flatten this vector # Create the equation # (x^{2} + y^{2})^2 - 2a^2*(x^{2}-y^{2}) <= 0 a=np.power(np.power(X[:,0]-5,2) + np.power(X[:,1]-5,2),2) b=np.power(X[:,0]-5,2) - np.power(X[:,1]-5,2) c= a - (b*np.power(4,2)) <=0 Y=c.reshape(2000,1) # Create a scatter plot of the lemniscate plt.scatter(X[:,0], X[:,1], c=Y, marker= 'o', s=15,cmap="viridis") Z=np.append(X,Y,axis=1) plt.savefig("fig50.png",bbox_inches='tight') plt.clf() # Set the data for classification X2=X.T Y2=Y.T # These settings work the best # Set the Deep Learning layer dimensions for a Relu activation layersDimensions = [2,7,4,1] #Execute the DL network parameters = L_Layer_DeepModel(X2, Y2, layersDimensions, hiddenActivationFunc='relu', learning_rate = 0.5,num_iterations = 10000, fig="fig5.png") #Plot the decision boundary plot_decision_boundary(lambda x: predict(parameters, x.T), X2, Y2,str(2.2),"fig6.png") # Compute the Confusion matrix yhat = predict(parameters,X2) from sklearn.metrics import confusion_matrix a=confusion_matrix(Y2.T,yhat.T) from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score print('Accuracy: {:.2f}'.format(accuracy_score(Y2.T, yhat.T))) print('Precision: {:.2f}'.format(precision_score(Y2.T, yhat.T))) print('Recall: {:.2f}'.format(recall_score(Y2.T, yhat.T))) print('F1: {:.2f}'.format(f1_score(Y2.T, yhat.T)))## Accuracy: 0.93 ## Precision: 0.77 ## Recall: 0.76 ## F1: 0.76


We could get better performance by tuning further. Do play around if you fork the code.
Note:: The lemniscate data is saved as a CSV and then read in R and also in Octave. I do this instead of recreating the lemniscate shape
3b. Classifying a lemniscate with Deep Learning Network – Relu activation(R code)
The R decision boundary for the Bernoulli’s lemniscate is shown below
Z <- as.matrix(read.csv("lemniscate.csv",header=FALSE))
Z1=data.frame(Z)
# Create a scatter plot of the lemniscate
ggplot(Z1,aes(x=V1,y=V2,col=V3)) +geom_point()#Set the data for the DL network
X=Z[,1:2]
Y=Z[,3]
X1=t(X)
Y1=t(Y)
# Set the layer dimensions for the tanh activation function
layersDimensions = c(2,5,4,1)
# Execute the Deep Learning network with Tanh activation
retvals = L_Layer_DeepModel(X1, Y1, layersDimensions,
hiddenActivationFunc='tanh',
learningRate = 0.3,
numIterations = 20000, print_cost = True)# Plot cost vs iteration
costs <- retvals[['costs']]
numIterations = 20000
iterations <- seq(0,numIterations,by=1000)
df <-data.frame(iterations,costs)
ggplot(df,aes(x=iterations,y=costs)) + geom_point() +geom_line(color="blue") +
xlab('No of iterations') + ylab('Cost') + ggtitle("Cost vs No of iterations")
#Plot the decision boundary
plotDecisionBoundary(Z,retvals,hiddenActivationFunc="tanh",0.3)
3c. Classifying a lemniscate with Deep Learning Network – Relu activation(Octave code)
Octave is used to generate the non-linear lemniscate boundary.
# Read the data
data=csvread("lemniscate.csv");
X=data(:,1:2);
Y=data(:,3);
# Set the dimensions of the layers
layersDimensions = [2 9 7 1]
# Compute the DL network
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='relu',
learningRate = 0.20,
numIterations = 10000);
plotCostVsIterations(10000,costs);
plotDecisionBoundary(data,weights, biases,hiddenActivationFunc="relu")


4a. Binary Classification using MNIST – Python code
Finally I perform a simple classification using the MNIST handwritten digits, which according to Prof Geoffrey Hinton is “the Drosophila of Deep Learning”.

The Python code for reading the MNIST data is taken from Alex Kesling’s github link MNIST.
In the Python code below, I perform a simple binary classification between the handwritten digit ‘5’ and ‘not 5’ which is all other digits. I will perform the proper classification of all digits using the Softmax classifier some time later.
import os
import numpy as np
import matplotlib.pyplot as plt
os.chdir("C:\\software\\DeepLearning-Posts\\part3")
execfile("./DLfunctions34.py")
execfile("./load_mnist.py")
training=list(read(dataset='training',path="./mnist"))
test=list(read(dataset='testing',path="./mnist"))
lbls=[]
pxls=[]
print(len(training))
# Select the first 10000 training data and the labels
for i in range(10000):
l,p=training[i]
lbls.append(l)
pxls.append(p)
labels= np.array(lbls)
pixels=np.array(pxls)
# Sey y=1 when labels == 5 and 0 otherwise
y=(labels==5).reshape(-1,1)
X=pixels.reshape(pixels.shape[0],-1)
# Create the necessary feature and target variable
X1=X.T
Y1=y.T
# Create the layer dimensions. The number of features are 28 x 28 = 784 since the 28 x 28
# pixels is flattened to single vector of length 784.
layersDimensions=[784, 15,9,7,1] # Works very well
parameters = L_Layer_DeepModel(X1, Y1, layersDimensions, hiddenActivationFunc='relu', learning_rate = 0.1,num_iterations = 1000, fig="fig7.png")
# Test data
lbls1=[]
pxls1=[]
for i in range(800):
l,p=test[i]
lbls1.append(l)
pxls1.append(p)
testLabels=np.array(lbls1)
testData=np.array(pxls1)
ytest=(testLabels==5).reshape(-1,1)
Xtest=testData.reshape(testData.shape[0],-1)
Xtest1=Xtest.T
Ytest1=ytest.T
yhat = predict(parameters,Xtest1)
from sklearn.metrics import confusion_matrix
a=confusion_matrix(Ytest1.T,yhat.T)
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print('Accuracy: {:.2f}'.format(accuracy_score(Ytest1.T, yhat.T)))
print('Precision: {:.2f}'.format(precision_score(Ytest1.T, yhat.T)))
print('Recall: {:.2f}'.format(recall_score(Ytest1.T, yhat.T)))
print('F1: {:.2f}'.format(f1_score(Ytest1.T, yhat.T)))
probs=predict_proba(parameters,Xtest1)
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(Ytest1.T, probs.T)
closest_zero = np.argmin(np.abs(thresholds))
closest_zero_p = precision[closest_zero]
closest_zero_r = recall[closest_zero]
plt.xlim([0.0, 1.01])
plt.ylim([0.0, 1.01])
plt.plot(precision, recall, label='Precision-Recall Curve')
plt.plot(closest_zero_p, closest_zero_r, 'o', markersize = 12, fillstyle = 'none', c='r', mew=3)
plt.xlabel('Precision', fontsize=16)
plt.ylabel('Recall', fontsize=16)
plt.savefig("fig8.png",bbox_inches='tight')
## Accuracy: 0.99
## Precision: 0.96
## Recall: 0.89
## F1: 0.92

In addition to plotting the Cost vs Iterations, I also plot the Precision-Recall curve to show how the Precision and Recall, which are complementary to each other vary with respect to the other. To know more about Precision-Recall, please check my post Practical Machine Learning with R and Python – Part 4.
Check out my compact and minimal book “Practical Machine Learning with R and Python:Second edition- Machine Learning in stereo” available in Amazon in paperback($10.99) and kindle($7.99) versions. My book includes implementations of key ML algorithms and associated measures and metrics. The book is ideal for anybody who is familiar with the concepts and would like a quick reference to the different ML algorithms that can be applied to problems and how to select the best model. Pick your copy today!!

A physical copy of the book is much better than scrolling down a webpage. Personally, I tend to use my own book quite frequently to refer to R, Python constructs, subsetting, machine Learning function calls and the necessary parameters etc. It is useless to commit any of this to memory, and a physical copy of a book is much easier to thumb through for the relevant code snippet. Pick up your copy today!
4b. Binary Classification using MNIST – R code
In the R code below the same binary classification of the digit ‘5’ and the ‘not 5’ is performed. The code to read and display the MNIST data is taken from Brendan O’ Connor’s github link at MNIST
source("mnist.R")
load_mnist()
#show_digit(train$x[2,]
layersDimensions=c(784, 7,7,3,1) # Works at 1500
x <- t(train$x)
# Choose only 5000 training data
x2 <- x[,1:5000]
y <-train$y
# Set labels for all digits that are 'not 5' to 0
y[y!=5] <- 0
# Set labels of digit 5 as 1
y[y==5] <- 1
# Set the data
y1 <- as.matrix(y)
y2 <- t(y1)
# Choose the 1st 5000 data
y3 <- y2[,1:5000]
#Execute the Deep Learning Model
retvals = L_Layer_DeepModel(x2, y3, layersDimensions,
hiddenActivationFunc='tanh',
learningRate = 0.3,
numIterations = 3000, print_cost = True)# Plot cost vs iteration
costs <- retvals[['costs']]
numIterations = 3000
iterations <- seq(0,numIterations,by=1000)
df <-data.frame(iterations,costs)
ggplot(df,aes(x=iterations,y=costs)) + geom_point() +geom_line(color="blue") +
xlab('No of iterations') + ylab('Cost') + ggtitle("Cost vs No of iterations")
# Compute probability scores
scores <- computeScores(retvals$parameters, x2,hiddenActivationFunc='relu')
a=y3==1
b=y3==0
# Compute probabilities of class 0 and class 1
class1=scores[a]
class0=scores[b]
# Plot ROC curve
pr <-pr.curve(scores.class0=class1,
scores.class1=class0,
curve=T)
plot(pr)

The AUC curve hugs the top left corner and hence the performance of the classifier is quite good.
4c. Binary Classification using MNIST – Octave code
This code to load MNIST data was taken from Daniel E blog.
Precision recall curves are available in Matlab but are yet to be implemented in Octave’s statistics package.
load('./mnist/mnist.txt.gz'); % load the dataset
# Subset the 'not 5' digits
a=(trainY != 5);
# Subset '5'
b=(trainY == 5);
#make a copy of trainY
#Set 'not 5' as 0 and '5' as 1
y=trainY;
y(a)=0;
y(b)=1;
X=trainX(1:5000,:);
Y=y(1:5000);
# Set the dimensions of layer
layersDimensions=[784, 7,7,3,1];
# Compute the DL network
[weights biases costs]=L_Layer_DeepModel(X', Y', layersDimensions,
hiddenActivationFunc='relu',
learningRate = 0.1,
numIterations = 5000);

Conclusion
It was quite a challenge coding a Deep Learning Network in Python, R and Octave. The Deep Learning network implementation, in this post,is the base Deep Learning network, without any of the regularization methods included. Here are some key learning that I got while playing with different multi-layer networks on different problems
a. Deep Learning Networks come with many levers, the hyper-parameters,
– learning rate
– activation unit
– number of hidden layers
– number of units per hidden layer
– number of iterations while performing gradient descent
b. Deep Networks are very sensitive. A change in any of the hyper-parameter makes it perform very differently
c. Initially I thought adding more hidden layers, or more units per hidden layer will make the DL network better at learning. On the contrary, there is a performance degradation after the optimal DL configuration
d. At a sub-optimal number of hidden layers or number of hidden units, gradient descent seems to get stuck at a local minima
e. There were occasions when the cost came down, only to increase slowly as the number of iterations were increased. Probably early stopping would have helped.
f. I also did come across situations of ‘exploding/vanishing gradient’, cost went to Inf/-Inf. Here I would think inclusion of ‘momentum method’ would have helped
I intend to add the additional hyper-parameters of L1, L2 regularization, momentum method, early stopping etc. into the code in my future posts.
Feel free to fork/clone the code from Github Deep Learning – Part 3, and take the DL network apart and play around with it.
I will be continuing this series with more hyper-parameters to handle vanishing and exploding gradients, early stopping and regularization in the weeks to come. I also intend to add some more activation functions to this basic Multi-Layer Network.
Hang around, there are more exciting things to come.
Watch this space!
References
1. Deep Learning Specialization
2. Neural Networks for Machine Learning
3. Deep Learning, Ian Goodfellow, Yoshua Bengio and Aaron Courville
4. Neural Networks: The mechanics of backpropagation
5. Machine Learning
Also see
1.My book ‘Practical Machine Learning with R and Python’ on Amazon
2. My travels through the realms of Data Science, Machine Learning, Deep Learning and (AI)
3. Designing a Social Web Portal
4. GooglyPlus: yorkr analyzes IPL players, teams, matches with plots and tables
4. Introducing QCSimulator: A 5-qubit quantum computing simulator in R
6. Presentation on “Intelligent Networks, CAMEL protocol, services & applications
7. Design Principles of Scalable, Distributed Systems
To see all posts see Index of posts