Introduction
My 5-qubit Quantum Computing Simulator,QCSimulator, is finally ready, and here it is! I have been able to successfully complete this simulator by working through a fair amount of material. To a large extent, the simulator is easy, if one understands how to solve the quantum circuit. However the theory behind quantum computing itself, is quite formidable, and I hope to scale this mountain over a period of time.
QCSimulator is now on CRAN!!!
The code for the QCSimulator package is also available at Github QCSimulator. This post has also been published at Rpubs as QCSimulator and can be downloaded as a PDF document at QCSimulator.pdf
Disclaimer: This article represents the author’s viewpoint only and doesn’t necessarily represent IBM’s positions, strategies or opinions
install.packages("QCSimulator")
library(QCSimulator)
library(ggplot2)1. Initialize the environment and set global variables
Here I initialize the environment with global variables and then display a few of them.
rm(list=ls())
#Call the init function to initialize the environment and create global variables
init()
# Display some of global variables in environment
ls()## [1] "I16" "I2" "I4" "I8" "q0_" "q00_" "q000_"
## [8] "q0000_" "q00000_" "q00001_" "q0001_" "q00010_" "q00011_" "q001_"
## [15] "q0010_" "q00100_" "q00101_" "q0011_" "q00110_" "q00111_" "q01_"
## [22] "q010_" "q0100_" "q01000_" "q01001_" "q0101_" "q01010_" "q01011_"
## [29] "q011_" "q0110_" "q01100_" "q01101_" "q0111_" "q01111_" "q1_"
## [36] "q10_" "q100_" "q1000_" "q10000_" "q10001_" "q1001_" "q10010_"
## [43] "q10011_" "q101_" "q1010_" "q10100_" "q10101_" "q1011_" "q10110_"
## [50] "q10111_" "q11_" "q110_" "q1100_" "q11000_" "q11001_" "q1101_"
## [57] "q11010_" "q11011_" "q111_" "q1110_" "q11100_" "q11101_" "q1111_"
## [64] "q11110_" "q11111_"#1. 2 x 2 Identity matrix
I2## [,1] [,2]
## [1,] 1 0
## [2,] 0 1#2. 8 x 8 Identity matrix
I8## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 1 0 0 0 0 0 0 0
## [2,] 0 1 0 0 0 0 0 0
## [3,] 0 0 1 0 0 0 0 0
## [4,] 0 0 0 1 0 0 0 0
## [5,] 0 0 0 0 1 0 0 0
## [6,] 0 0 0 0 0 1 0 0
## [7,] 0 0 0 0 0 0 1 0
## [8,] 0 0 0 0 0 0 0 1#3. Qubit |00>
q00_## [,1]
## [1,] 1
## [2,] 0
## [3,] 0
## [4,] 0#4. Qubit |010>
q010_## [,1]
## [1,] 0
## [2,] 0
## [3,] 1
## [4,] 0
## [5,] 0
## [6,] 0
## [7,] 0
## [8,] 0#5. Qubit |0100>
q0100_## [,1]
## [1,] 0
## [2,] 0
## [3,] 0
## [4,] 0
## [5,] 1
## [6,] 0
## [7,] 0
## [8,] 0
## [9,] 0
## [10,] 0
## [11,] 0
## [12,] 0
## [13,] 0
## [14,] 0
## [15,] 0
## [16,] 0#6. Qubit 10010
q10010_## [,1]
## [1,] 0
## [2,] 0
## [3,] 0
## [4,] 0
## [5,] 0
## [6,] 0
## [7,] 0
## [8,] 0
## [9,] 0
## [10,] 0
## [11,] 0
## [12,] 0
## [13,] 0
## [14,] 0
## [15,] 0
## [16,] 0
## [17,] 0
## [18,] 0
## [19,] 1
## [20,] 0
## [21,] 0
## [22,] 0
## [23,] 0
## [24,] 0
## [25,] 0
## [26,] 0
## [27,] 0
## [28,] 0
## [29,] 0
## [30,] 0
## [31,] 0
## [32,] 0The QCSimulator implements the following gates
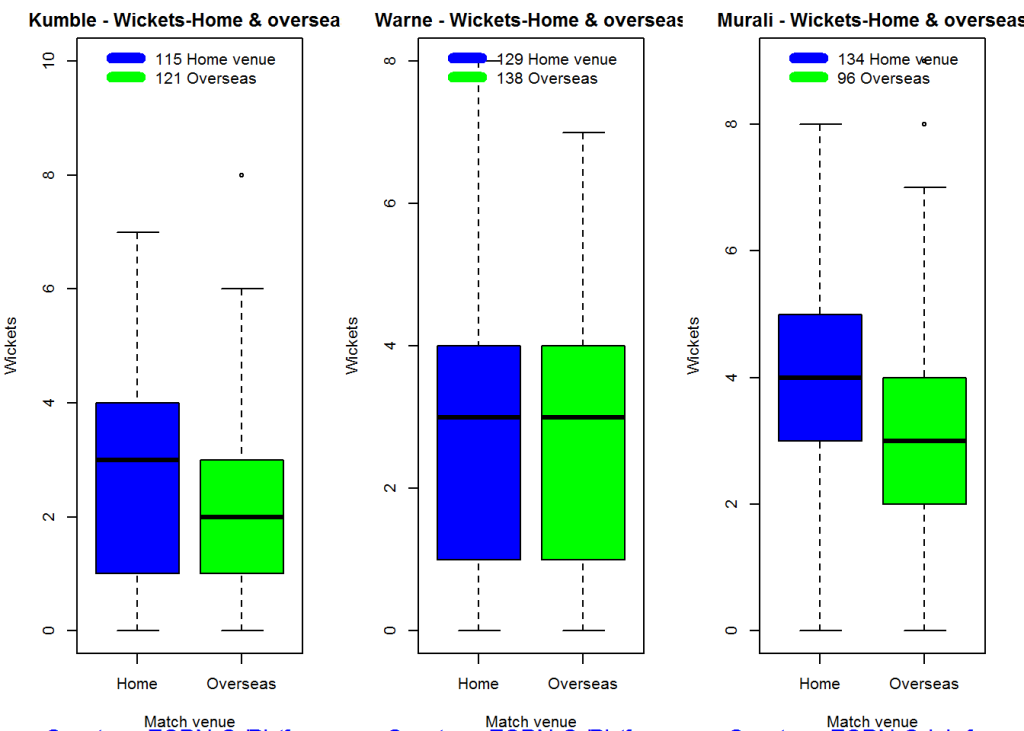
- Pauli X,Y,Z, S,S’, T, T’ gates
- Rotation , Hadamard,CSWAP,Toffoli gates
- 2,3,4,5 qubit CNOT gates e.g CNOT2_01,CNOT3_20,CNOT4_13 etc
- Toffoli State,SWAPQ0Q1
2. To display the unitary matrix of gates
To check the unitary matrix of gates, we need to pass the appropriate identity matrix as an argument. Hence below the qubit gates require a 2 x 2 unitary matrix and the 2 & 3 qubit CNOT gates require a 4 x 4 and 8 x 8 identity matrix respectively
PauliX(I2)## [,1] [,2]
## [1,] 0 1
## [2,] 1 0Hadamard(I2)## [,1] [,2]
## [1,] 0.7071068 0.7071068
## [2,] 0.7071068 -0.7071068S1Gate(I2)## [,1] [,2]
## [1,] 1+0i 0+0i
## [2,] 0+0i 0-1iCNOT2_10(I4)## [,1] [,2] [,3] [,4]
## [1,] 1 0 0 0
## [2,] 0 0 0 1
## [3,] 0 0 1 0
## [4,] 0 1 0 0CNOT3_20(I8)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,] 1 0 0 0 0 0 0 0
## [2,] 0 0 0 0 0 1 0 0
## [3,] 0 0 1 0 0 0 0 0
## [4,] 0 0 0 0 0 0 0 1
## [5,] 0 0 0 0 1 0 0 0
## [6,] 0 1 0 0 0 0 0 0
## [7,] 0 0 0 0 0 0 1 0
## [8,] 0 0 0 1 0 0 0 03. Compute the inner product of vectors
For example of phi = 1/2|0> + sqrt(3)/2|1> and si= 1/sqrt(2)(10> + |1>) then the inner product is the dot product of the vectors
phi = matrix(c(1/2,sqrt(3)/2),nrow=2,ncol=1)
si = matrix(c(1/sqrt(2),1/sqrt(2)),nrow=2,ncol=1)
angle= innerProduct(phi,si)
cat("Angle between vectors is:",angle)## Angle between vectors is: 154. Compute the dagger function for a gate
The gate dagger computes and displays the transpose of the complex conjugate of the matrix
TGate(I2)## [,1] [,2]
## [1,] 1+0i 0.0000000+0.0000000i
## [2,] 0+0i 0.7071068+0.7071068iGateDagger(TGate(I2))## [,1] [,2]
## [1,] 1+0i 0.0000000+0.0000000i
## [2,] 0+0i 0.7071068-0.7071068i5. Invoking gates in series
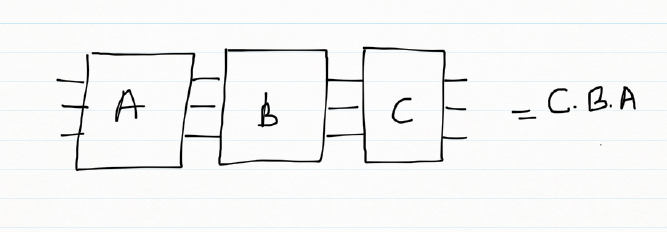
The Quantum gates can be chained by passing each preceding Quantum gate as the argument. The final gate in the chain will have the qubit or the identity matrix passed to it.
# Call in reverse order
# Superposition states
# |+> state
Hadamard(q0_)## [,1]
## [1,] 0.7071068
## [2,] 0.7071068# |-> ==> H x Z
PauliZ(Hadamard(q0_))## [,1]
## [1,] 0.7071068
## [2,] -0.7071068# (+i) Y ==> H x S
SGate(Hadamard(q0_))## [,1]
## [1,] 0.7071068+0.0000000i
## [2,] 0.0000000+0.7071068i# (-i)Y ==> H x S1
S1Gate(Hadamard(q0_))## [,1]
## [1,] 0.7071068+0.0000000i
## [2,] 0.0000000-0.7071068i# Q1 -- TGate- Hadamard
Q1 = Hadamard(TGate(I2))6. More gates in series
TGate of depth 2
The Quantum circuit for a TGate of Depth 2 is
Q0 — Hadamard-TGate-Hadamard-TGate-SGate-Measurement as shown in IBM’s Quantum Experience Composer
Implementing the quantum gates in series in reverse order we have
# Invoking this in reverse order we get
a = SGate(TGate(Hadamard(TGate(Hadamard(q0_)))))
result=measurement(a)
plotMeasurement(result)7. Invoking gates in parallel
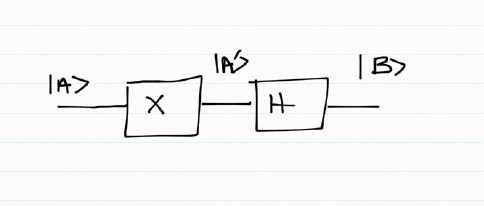
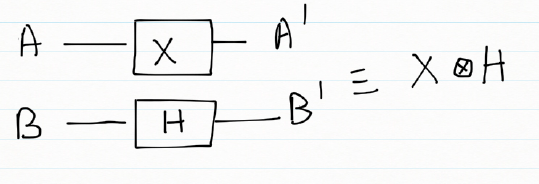
To obtain the results of gates in parallel we have to take the Tensor Product Note:In the TensorProduct invocation the Identity matrix is passed as an argument to get the unitary matrix of the gate. Q0 – Hadamard-Measurement Q1 – Identity- Measurement
#
a = TensorProd(Hadamard(I2),I2)
b = DotProduct(a,q00_)
plotMeasurement(measurement(b))a = TensorProd(PauliZ(I2),Hadamard(I2))
b = DotProduct(a,q00_)
plotMeasurement(measurement(b))8. Measurement
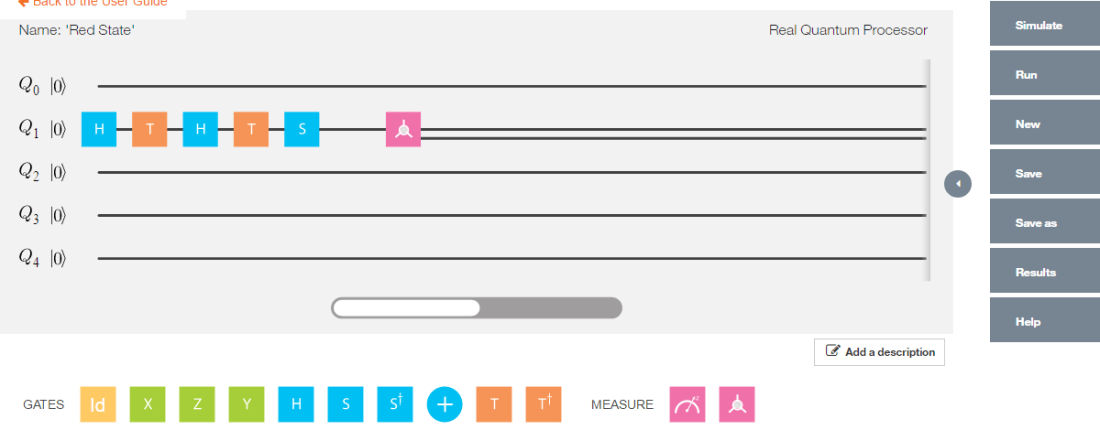
The measurement of a Quantum circuit can be obtained using the measurement function. Consider the following Quantum circuit
Q0 – H-T-H-T-S-H-T-H-T-H-T-H-S-Measurement where H – Hadamard gate, T – T Gate and S- S Gate
a = SGate(Hadamard(TGate(Hadamard(TGate(Hadamard(TGate(Hadamard(SGate(TGate(Hadamard(TGate(Hadamard(I2)))))))))))))
measurement(a)## 0 1
## v 0.890165 0.1098359. Plot measurement
Using the same example as above Q0 – H-T-H-T-S-H-T-H-T-H-T-H-S-Measurement where H – Hadamard gate, T – T Gate and S- S Gate we can plot the measurement
a = SGate(Hadamard(TGate(Hadamard(TGate(Hadamard(TGate(Hadamard(SGate(TGate(Hadamard(TGate(Hadamard(I2)))))))))))))
result = measurement(a)
plotMeasurement(result)10. Evaluating a Quantum Circuit
The above procedures for evaluating a quantum gates in series and parallel can be used to evalute more complex quantum circuits where the quantum gates are in series and in parallel.
Here is an evaluation of one such circuit, the Bell ZQ state using the QCSimulator (from IBM’s Quantum Experience)
# 1st composite
a = TensorProd(Hadamard(I2),I2)
# Output of CNOT
b = CNOT2_01(a)
# 2nd series
c=Hadamard(TGate(Hadamard(SGate(I2))))
#3rd composite
d= TensorProd(I2,c)
# Output of 2nd composite
e = DotProduct(b,d)
#Action of quantum circuit on |00>
f = DotProduct(e,q00_)
result= measurement(f)
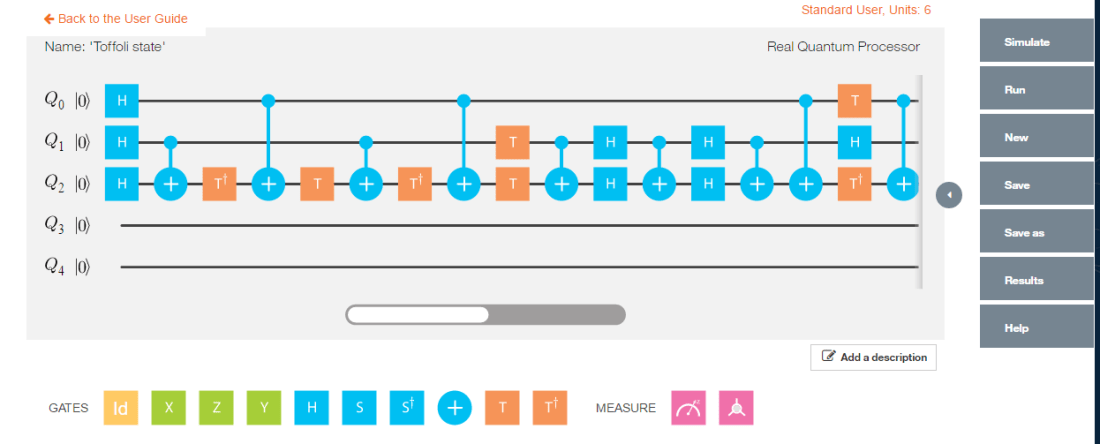
plotMeasurement(result)11. Toffoli State
This circuit for this comes from IBM’s Quantum Experience. This circuit is available in the package. This is how the state was constructed. This circuit is shown below
The implementation of the above circuit in QCSimulator is as below
# Computation of the Toffoli State
H=1/sqrt(2) * matrix(c(1,1,1,-1),nrow=2,ncol=2)
I=matrix(c(1,0,0,1),nrow=2,ncol=2)
# 1st composite
# H x H x H
a = TensorProd(TensorProd(H,H),H)
# 1st CNOT
a1= CNOT3_12(a)
# 2nd composite
# I x I x T1Gate
b = TensorProd(TensorProd(I,I),T1Gate(I))
b1 = DotProduct(b,a1)
c = CNOT3_02(b1)
# 3rd composite
# I x I x TGate
d = TensorProd(TensorProd(I,I),TGate(I))
d1 = DotProduct(d,c)
e = CNOT3_12(d1)
# 4th composite
# I x I x T1Gate
f = TensorProd(TensorProd(I,I),T1Gate(I))
f1 = DotProduct(f,e)
g = CNOT3_02(f1)
#5th composite
# I x T x T
h = TensorProd(TensorProd(I,TGate(I)),TGate(I))
h1 = DotProduct(h,g)
i = CNOT3_12(h1)
#6th composite
# I x H x H
j = TensorProd(TensorProd(I,Hadamard(I)),Hadamard(I))
j1 = DotProduct(j,i)
k = CNOT3_12(j1)
# 7th composite
# I x H x H
l = TensorProd(TensorProd(I,Hadamard(I)),Hadamard(I))
l1 = DotProduct(l,k)
m = CNOT3_12(l1)
n = CNOT3_02(m)
#8th composite
# T x H x T1
o = TensorProd(TensorProd(TGate(I),Hadamard(I)),T1Gate(I))
o1 = DotProduct(o,n)
p = CNOT3_02(o1)
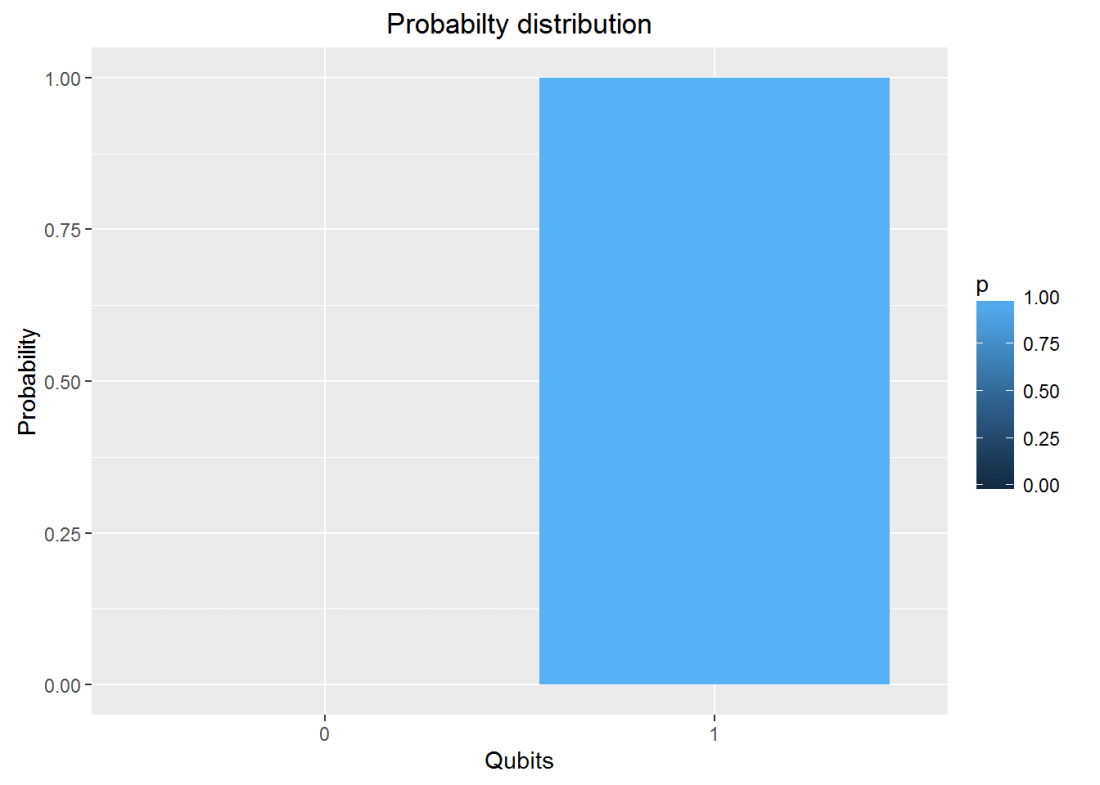
result = measurement(p)
plotMeasurement(result)12. GHZ YYX measurement
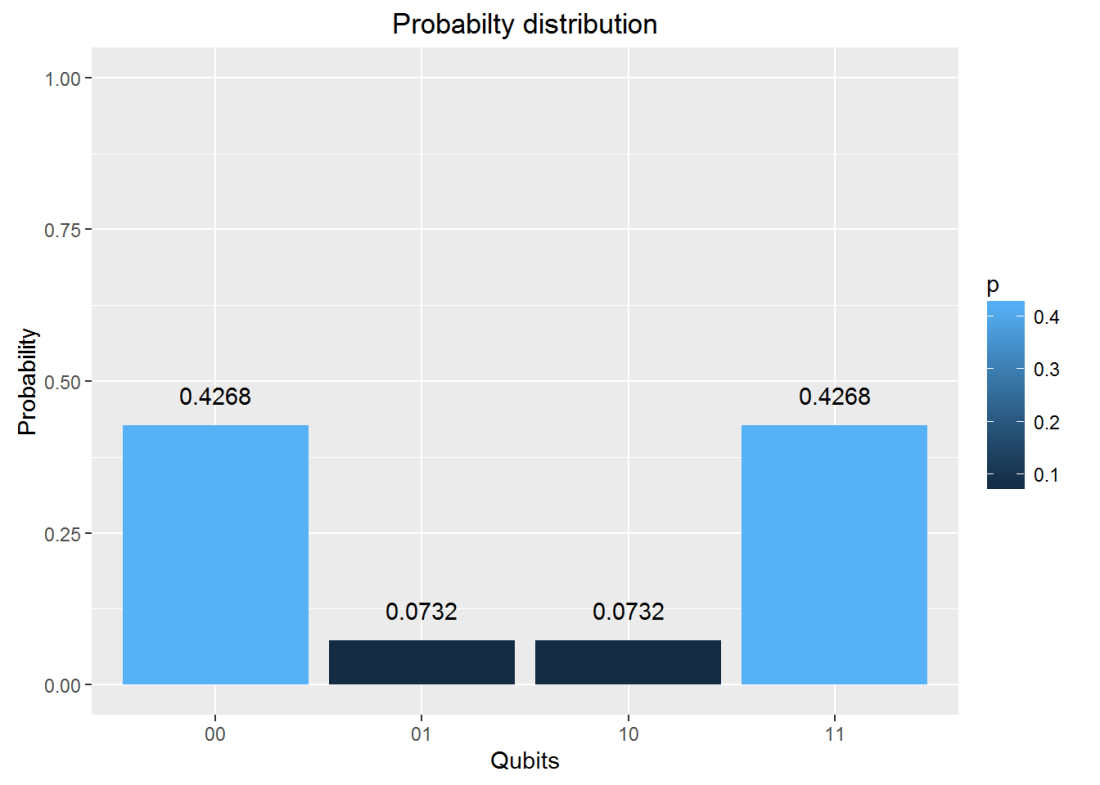
Here is another Quantum circuit, namely the entangled GHZ YYX state. This is
and is implemented in QCSimulator as
# Composite 1
a = TensorProd(TensorProd(Hadamard(I2),Hadamard(I2)),PauliX(I2))
b= CNOT3_12(a)
c= CNOT3_02(b)
# Composite 2
d= TensorProd(TensorProd(Hadamard(I2),Hadamard(I2)),Hadamard(I2))
e= DotProduct(d,c)
#Composite 3
f= TensorProd(TensorProd(S1Gate(I2),S1Gate(I2)),Hadamard(I2))
g= DotProduct(f,e)
#Composite 4
i= TensorProd(TensorProd(Hadamard(I2),Hadamard(I2)),I2)
j = DotProduct(i,g)
result=measurement(j)
plotMeasurement(result)Conclusion
The 5 qubit Quantum Computing Simulator is now fully functional. I hope to add more gates and functionality in the months to come.
Feel free to install the package from Github and give it a try.
Disclaimer: This article represents the author’s viewpoint only and doesn’t necessarily represent IBM’s positions, strategies or opinions
References
- IBM’s Quantum Experience
- Quantum Computing in Python by Dr. Christine Corbett Moran
- Lecture notes-1
- Lecture notes-2
- Quantum Mechanics and Quantum Computationat edX- UC, Berkeley
My other posts on Quantum Computing
- Venturing into IBM’s Quantum Experience 2.Going deeper into IBM’s Quantum Experience!
- A primer on Qubits, Quantum gates and Quantum Operations
- Exploring Quantum Gate operations with QCSimulator
- Taking a closer look at Quantum gates and their operations
You may also like
For more posts on other topics like Cloud Computing, IBM Bluemix, Distributed Computing, OpenCV, R, cricket please check my Index of posts










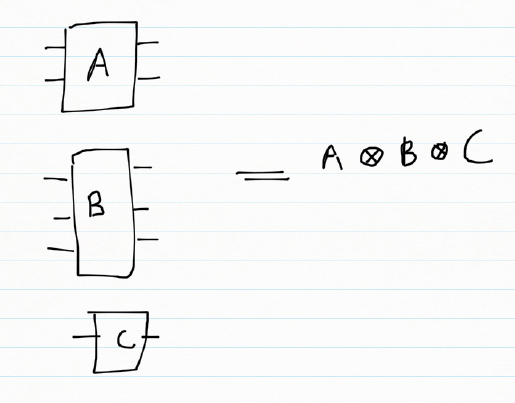
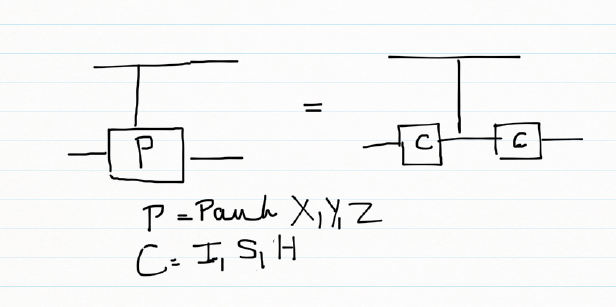









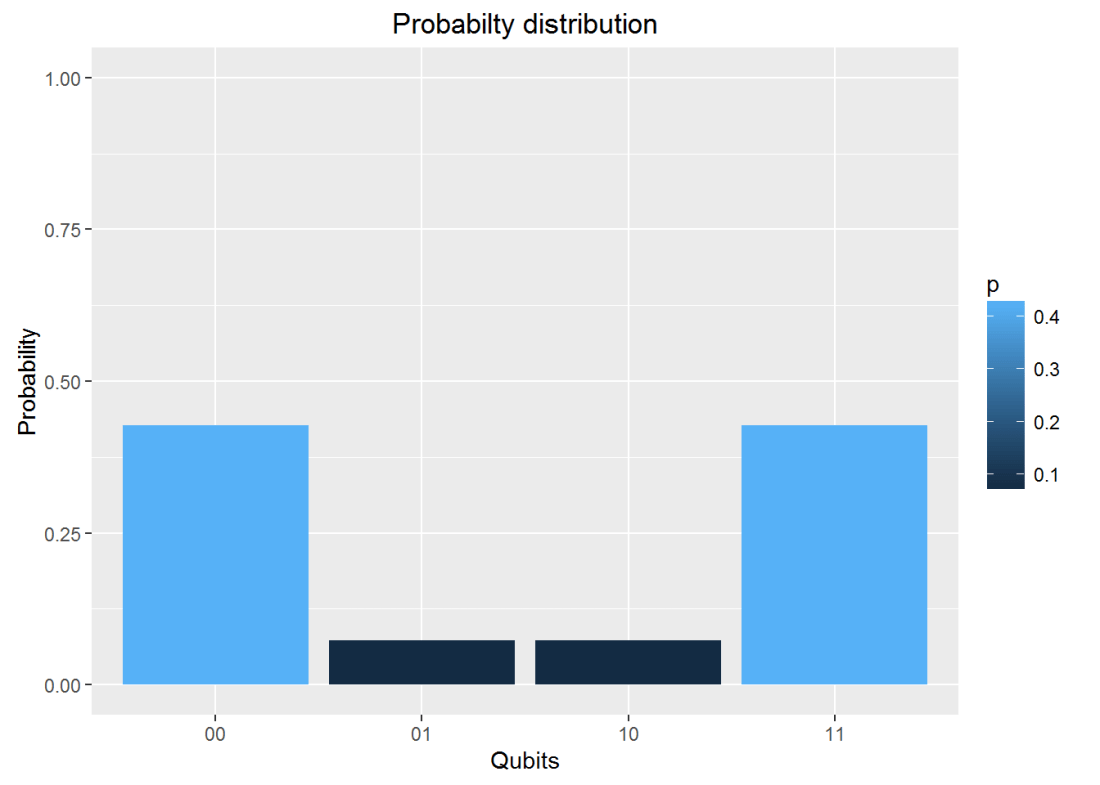

























 Checkout my book ‘Deep Learning from first principles Second Edition- In vectorized Python, R and Octave’. My book is available on Amazon as
Checkout my book ‘Deep Learning from first principles Second Edition- In vectorized Python, R and Octave’. My book is available on Amazon as