Take 4+: Presentations on ‘Elements of Neural Networks and Deep Learning’ – Parts 1-8

“Lights, camera and … action – Take 4+!”

This post includes a rework of all presentation of ‘Elements of Neural Networks and Deep Learning Parts 1-8 ‘ since my earlier presentations had some missing parts, omissions and some occasional errors. So I have re-recorded all the presentations.
This series of presentation will do a deep-dive into Deep Learning networks starting from the fundamentals. The equations required for performing learning in a L-layer Deep Learning network are derived in detail, starting from the basics. Further, the presentations also discuss multi-class classification, regularization techniques, and gradient descent optimization methods in deep networks methods. Finally the presentations also touch on how Deep Learning Networks can be tuned.

The corresponding implementations are available in vectorized R, Python and Octave are available in my book ‘Deep Learning from first principles:Second edition- In vectorized Python, R and Octave‘

1. Elements of Neural Networks and Deep Learning – Part 1
This presentation introduces Neural Networks and Deep Learning. A look at history of Neural Networks, Perceptrons and why Deep Learning networks are required and concluding with a simple toy examples of a Neural Network and how they compute. This part also includes a small digression on the basics of Machine Learning and how the algorithm learns from a data set

2. Elements of Neural Networks and Deep Learning – Part 2
This presentation takes logistic regression as an example and creates an equivalent 2 layer Neural network. The presentation also takes a look at forward & backward propagation and how the cost is minimized using gradient descent

The implementation of the discussed 2 layer Neural Network in vectorized R, Python and Octave are available in my post ‘Deep Learning from first principles in Python, R and Octave – Part 1‘

3. Elements of Neural Networks and Deep Learning – Part 3
This 3rd part, discusses a primitive neural network with an input layer, output layer and a hidden layer. The neural network uses tanh activation in the hidden layer and a sigmoid activation in the output layer. The equations for forward and backward propagation are derived.

To see the implementations for the above discussed video see my post ‘Deep Learning from first principles in Python, R and Octave – Part 2‘

4. Elements of Neural Network and Deep Learning – Part 4
This presentation is a continuation of my 3rd presentation in which I derived the equations for a simple 3 layer Neural Network with 1 hidden layer. In this video presentation, I discuss step-by-step the derivations for a L-Layer, multi-unit Deep Learning Network, with any activation function g(z)

The implementations of L-Layer, multi-unit Deep Learning Network in vectorized R, Python and Octave are available in my post Deep Learning from first principles in Python, R and Octave – Part 3

5. Elements of Neural Network and Deep Learning – Part 5
This presentation discusses multi-class classification using the Softmax function. The detailed derivation for the Jacobian of the Softmax is discussed, and subsequently the derivative of cross-entropy loss is also discussed in detail. Finally the final set of equations for a Neural Network with multi-class classification is derived.

The corresponding implementations in vectorized R, Python and Octave are available in the following posts
a. Deep Learning from first principles in Python, R and Octave – Part 4
b. Deep Learning from first principles in Python, R and Octave – Part 5

6. Elements of Neural Networks and Deep Learning – Part 6
This part discusses initialization methods specifically like He and Xavier. The presentation also focuses on how to prevent over-fitting using regularization. Lastly the dropout method of regularization is also discussed

The corresponding implementations in vectorized R, Python and Octave of the above discussed methods are available in my post Deep Learning from first principles in Python, R and Octave – Part 6

7. Elements of Neural Networks and Deep Learning – Part 7
This presentation introduces exponentially weighted moving average and shows how this is used in different approaches to gradient descent optimization. The key techniques discussed are learning rate decay, momentum method, rmsprop and adam.

The equivalent implementations of the gradient descent optimization techniques in R, Python and Octave can be seen in my post Deep Learning from first principles in Python, R and Octave – Part 7

8. Elements of Neural Networks and Deep Learning – Part 8
This last part touches on the method to adopt while tuning hyper-parameters in Deep Learning networks

Checkout my book ‘Deep Learning from first principles: Second Edition – In vectorized Python, R and Octave’. My book starts with the implementation of a simple 2-layer Neural Network and works its way to a generic L-Layer Deep Learning Network, with all the bells and whistles. The derivations have been discussed in detail. The code has been extensively commented and included in its entirety in the Appendix sections. My book is available on Amazon as paperback ($18.99) and in kindle version($9.99/Rs449).

This concludes this series of presentations on “Elements of Neural Networks and Deep Learning’

Also
1. My book ‘Practical Machine Learning in R and Python: Third edition’ on Amazon
2. Introducing cricpy:A python package to analyze performances of cricketers
3. Natural language processing: What would Shakespeare say?
4. Big Data-2: Move into the big league:Graduate from R to SparkR
5. Presentation on Wireless Technologies – Part 1
6. Introducing cricketr! : An R package to analyze performances of cricketers

To see all posts click Index of posts

My presentations on ‘Elements of Neural Networks & Deep Learning’ -Parts 4,5

This is the next set of presentations on “Elements of Neural Networks and Deep Learning”. In the 4th presentation I discuss and derive the generalized equations for a multi-unit, multi-layer Deep Learning network. The 5th presentation derives the equations for a Deep Learning network when performing multi-class classification along with the derivations for cross-entropy loss. The corresponding implementations are available in vectorized R, Python and Octave are available in my book ‘Deep Learning from first principles:Second edition- In vectorized Python, R and Octave‘

Important note: Do check out my later version of these videos at Take 4+: Presentations on ‘Elements of Neural Networks and Deep Learning’ – Parts 1-8 . These have more content and also include some corrections. Check it out!

1. Elements of Neural Network and Deep Learning – Part 4
This presentation is a continuation of my 3rd presentation in which I derived the equations for a simple 3 layer Neural Network with 1 hidden layer. In this video presentation, I discuss step-by-step the derivations for a L-Layer, multi-unit Deep Learning Network, with any activation function g(z)

The implementations of L-Layer, multi-unit Deep Learning Network in vectorized R, Python and Octave are available in my post Deep Learning from first principles in Python, R and Octave – Part 3

2. Elements of Neural Network and Deep Learning – Part 5
This presentation discusses multi-class classification using the Softmax function. The detailed derivation for the Jacobian of the Softmax is discussed, and subsequently the derivative of cross-entropy loss is also discussed in detail. Finally the final set of equations for a Neural Network with multi-class classification is derived.

To be continued. Watch this space!

Also see
1. My book ‘Practical Machine Learning in R and Python: Third edition’ on Amazon
2. Big Data-2: Move into the big league:Graduate from R to SparkR
3. Introducing QCSimulator: A 5-qubit quantum computing simulator in R
4. My TEDx talk on the “Internet of Things
5. Rock N’ Roll with Bluemix, Cloudant & NodeExpress
6. GooglyPlus: yorkr analyzes IPL players, teams, matches with plots and tables
7. Literacy in India – A deepR dive
8. Fun simulation of a Chain in Android

To see all posts click Index of Posts

My book ‘Deep Learning from first principles:Second Edition’ now on Amazon

The second edition of my book ‘Deep Learning from first principles:Second Edition- In vectorized Python, R and Octave’, is now available on Amazon, in both paperback ($18.99) and kindle ($9.99/Rs449/-) versions. Since this book is almost 70% code, all functions, and code snippets have been formatted to use the fixed-width font ‘Lucida Console’. In addition line numbers have been added to all code snippets. This makes the code more organized and much more readable. I have also fixed typos in the book

Untitled

You can download the PDF version of this book from Github at https://github.com/tvganesh/DeepLearningBook-2ndEd

The book includes the following chapters

Table of Contents
Preface 4
Introduction 6
1. Logistic Regression as a Neural Network 8
2. Implementing a simple Neural Network 23
3. Building a L- Layer Deep Learning Network 48
4. Deep Learning network with the Softmax 85
5. MNIST classification with Softmax 103
6. Initialization, regularization in Deep Learning 121
7. Gradient Descent Optimization techniques 167
8. Gradient Check in Deep Learning 197
1. Appendix A 214
2. Appendix 1 – Logistic Regression as a Neural Network 220
3. Appendix 2 - Implementing a simple Neural Network 227
4. Appendix 3 - Building a L- Layer Deep Learning Network 240
5. Appendix 4 - Deep Learning network with the Softmax 259
6. Appendix 5 - MNIST classification with Softmax 269
7. Appendix 6 - Initialization, regularization in Deep Learning 302
8. Appendix 7 - Gradient Descent Optimization techniques 344
9. Appendix 8 – Gradient Check 405
References 475

Also see
1. My book ‘Practical Machine Learning in R and Python: Second edition’ on Amazon
2. The 3rd paperback & kindle editions of my books on Cricket, now on Amazon
3. De-blurring revisited with Wiener filter using OpenCV
4. TWS-4: Gossip protocol: Epidemics and rumors to the rescue
5. A Cloud medley with IBM Bluemix, Cloudant DB and Node.js
6. Practical Machine Learning with R and Python – Part 6
7. GooglyPlus: yorkr analyzes IPL players, teams, matches with plots and tables
8. Fun simulation of a Chain in Android

To see posts click Index of Posts

Deep Learning from first principles in Python, R and Octave – Part 4

In this 4th post of my series on Deep Learning from first principles in Python, R and Octave – Part 4, I explore the details of creating a multi-class classifier using the Softmax activation unit in a neural network. The earlier posts in this series were

1. Deep Learning from first principles in Python, R and Octave – Part 1. In this post I implemented logistic regression as a simple Neural Network in vectorized Python, R and Octave
2. Deep Learning from first principles in Python, R and Octave – Part 2. This 2nd part implemented the most elementary neural network with 1 hidden layer and any number of activation units in the hidden layer with sigmoid activation at the output layer
3. Deep Learning from first principles in Python, R and Octave – Part 3. The 3rd implemented a multi-layer Deep Learning network with an arbitrary number if hidden layers and activation units per hidden layer. The output layer was for binary classification which was based on the sigmoid unit. This multi-layer deep network was implemented in vectorized Python, R and Octave.

You can download the PDF version of this book from Github at https://github.com/tvganesh/DeepLearningBook-2ndEd

This 4th part takes a swing at multi-class classification and uses the Softmax as the activation unit in the output layer. Inclusion of the Softmax activation unit in the activation layer requires us to compute the derivative of Softmax, or rather the “Jacobian” of the Softmax function, besides also computing the log loss for this Softmax activation during back propagation. Since the derivation of the Jacobian of a Softmax and the computation of the Cross Entropy/log loss is very involved, I have implemented a basic neural network with just 1 hidden layer with the Softmax activation at the output layer. I also perform multi-class classification based on the ‘spiral’ data set from CS231n Convolutional Neural Networks Stanford course, to test the performance and correctness of the implementations in Python, R and Octave. You can clone download the code for the Python, R and Octave implementations from Github at Deep Learning – Part 4

Note: A detailed discussion of the derivation below can also be seen in my video presentation Neural Networks 5

The Softmax function takes an N dimensional vector as input and generates a N dimensional vector as output.
The Softmax function is given by
$S_{j}= \frac{e_{j}}{\sum_{i}^{N}e_{k}}$
There is a probabilistic interpretation of the Softmax, since the sum of the Softmax values of a set of vectors will always add up to 1, given that each Softmax value is divided by the total of all values.

As mentioned earlier, the Softmax takes a vector input and returns a vector of outputs. For e.g. the Softmax of a vector a=[1, 3, 6] is another vector S=[0.0063,0.0471,0.9464]. Notice that vector output is proportional to the input vector. Also, taking the derivative of a vector by another vector, is known as the Jacobian. By the way, The Matrix Calculus You Need For Deep Learning by Terence Parr and Jeremy Howard, is very good paper that distills all the main mathematical concepts for Deep Learning in one place.

Let us take a simple 2 layered neural network with just 2 activation units in the hidden layer is shown below

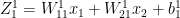
$Z_{1}^{1} =W_{11}^{1}x_{1} + W_{21}^{1}x_{2} + b_{1}^{1}$
$Z_{2}^{1} =W_{12}^{1}x_{1} + W_{22}^{1}x_{2} + b_{2}^{1}$
and
$A_{1}^{1} = g'(Z_{1}^{1})$
$A_{2}^{1} = g'(Z_{2}^{1})$
where g'() is the activation unit in the hidden layer which can be a relu, sigmoid or a
tanh function

Note: The superscript denotes the layer. The above denotes the equation for layer 1
of the neural network. For layer 2 with the Softmax activation, the equations are
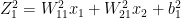
$Z_{1}^{2} =W_{11}^{2}x_{1} + W_{21}^{2}x_{2} + b_{1}^{2}$
$Z_{2}^{2} =W_{12}^{2}x_{1} + W_{22}^{2}x_{2} + b_{2}^{2}$
and
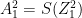
$A_{1}^{2} = S(Z_{1}^{2})$
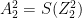
$A_{2}^{2} = S(Z_{2}^{2})$
where S() is the Softmax activation function
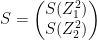
$S=\begin{pmatrix} S(Z_{1}^{2})\\ S(Z_{2}^{2}) \end{pmatrix}$
$S=\begin{pmatrix} \frac{e^{Z1}}{e^{Z1}+e^{Z2}}\\ \frac{e^{Z2}}{e^{Z1}+e^{Z2}} \end{pmatrix}$

The Jacobian of the softmax ‘S’ is given by
$\begin{pmatrix} \frac {\partial S_{1}}{\partial Z_{1}} & \frac {\partial S_{1}}{\partial Z_{2}}\\ \frac {\partial S_{2}}{\partial Z_{1}} & \frac {\partial S_{2}}{\partial Z_{2}} \end{pmatrix}$
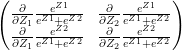$\begin{pmatrix} \frac{\partial}{\partial Z_{1}} \frac {e^{Z1}}{e^{Z1}+ e^{Z2}} & \frac{\partial}{\partial Z_{2}} \frac {e^{Z1}}{e^{Z1}+ e^{Z2}}\\ \frac{\partial}{\partial Z_{1}} \frac {e^{Z2}}{e^{Z1}+ e^{Z2}} & \frac{\partial}{\partial Z_{2}} \frac {e^{Z2}}{e^{Z1}+ e^{Z2}} \end{pmatrix}$ – (A)

Now the ‘division-rule’ of derivatives is as follows. If u and v are functions of x, then
$\frac{d}{dx} \frac {u}{v} =\frac {vdu -udv}{v^{2}}$
Using this to compute each element of the above Jacobian matrix, we see that
when i=j we have
$\frac {\partial}{\partial Z1}\frac{e^{Z1}}{e^{Z1}+e^{Z2}} = \frac {\sum e^{Z1} - e^{Z1^{2}}}{\sum ^{2}}$
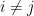
and when $i \neq j$
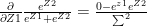
$\frac {\partial}{\partial Z1}\frac{e^{Z2}}{e^{Z1}+e^{Z2}} = \frac {0 - e^{z1}e^{Z2}}{\sum ^{2}}$
This is of the general form
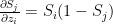$\frac {\partial S_{j}}{\partial z_{i}} = S_{i}( 1-S_{j})$ when i=j
and
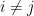
$\frac {\partial S_{j}}{\partial z_{i}} = -S_{i}S_{j}$ when $i \neq j$
Note: Since the Softmax essentially gives the probability the following
notation is also used
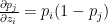$\frac {\partial p_{j}}{\partial z_{i}} = p_{i}( 1-p_{j})$ when i=j
and
$\frac {\partial p_{j}}{\partial z_{i}} = -p_{i}p_{j} when i \neq j$
If you throw the “Kronecker delta” into the equation, then the above equations can be expressed even more concisely as
$\frac {\partial p_{j}}{\partial z_{i}} = p_{i} (\delta_{ij} - p_{j})$
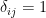where $\delta_{ij} = 1$ when i=j and 0 when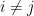 $i \neq j$

This reduces the Jacobian of the simple 2 output softmax vectors equation (A) as
$\begin{pmatrix} p_{1}(1-p_{1}) & -p_{1}p_{2} \\ -p_{2}p_{1} & p_{2}(1-p_{2}) \end{pmatrix}$
The loss of Softmax is given by
$L = -\sum y_{i} log(p_{i})$
For the 2 valued Softmax output this is
$\frac {dL}{dp1} = -\frac {y_{1}}{p_{1}}$
$\frac {dL}{dp2} = -\frac {y_{2}}{p_{2}}$
Using the chain rule we can write
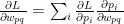$\frac {\partial L}{\partial w_{pq}} = \sum _{i}\frac {\partial L}{\partial p_{i}} \frac {\partial p_{i}}{\partial w_{pq}}$ (1)
and
$\frac {\partial p_{i}}{\partial w_{pq}} = \sum _{k}\frac {\partial p_{i}}{\partial z_{k}} \frac {\partial z_{k}}{\partial w_{pq}}$ (2)
In expanded form this is
$\frac {\partial L}{\partial w_{pq}} = \sum _{i}\frac {\partial L}{\partial p_{i}} \sum _{k}\frac {\partial p_{i}}{\partial z_{k}} \frac {\partial z_{k}}{\partial w_{pq}}$
Also
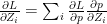
$\frac {\partial L}{\partial Z_{i}} =\sum _{i} \frac {\partial L}{\partial p} \frac {\partial p}{\partial Z_{i}}$
Therefore
$\frac {\partial L}{\partial Z_{1}} =\frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial Z_{1}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial Z_{1}}$
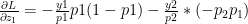
$\frac {\partial L}{\partial z_{1}}=-\frac {y1}{p1} p1(1-p1) - \frac {y2}{p2}*(-p_{2}p_{1})$
Since
$\frac {\partial p_{j}}{\partial z_{i}} = p_{i}( 1-p_{j})$ when i=j
and
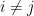
$\frac {\partial p_{j}}{\partial z_{i}} = -p_{i}p_{j}$ when $i \neq j$
which simplifies to
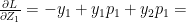
$\frac {\partial L}{\partial Z_{1}} = -y_{1} + y_{1}p_{1} + y_{2}p_{1} =$
$p_{1}\sum (y_{1} + y_2) - y_{1}$
$\frac {\partial L}{\partial Z_{1}}= p_{1} - y_{1}$
Since
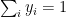
$\sum_{i} y_{i} =1$
Similarly
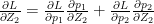
$\frac {\partial L}{\partial Z_{2}} =\frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial Z_{2}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial Z_{2}}$
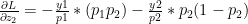
$\frac {\partial L}{\partial z_{2}}=-\frac {y1}{p1}*(p_{1}p_{2}) - \frac {y2}{p2}*p_{2}(1-p_{2})$
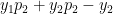
$y_{1}p_{2} + y_{2}p_{2} - y_{2}$
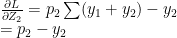
$\frac {\partial L}{\partial Z_{2}} =p_{2}\sum (y_{1} + y_2) - y_{2}\\ = p_{2} - y_{2}$
In general this is of the form
$\frac {\partial L}{\partial z_{i}} = p_{i} -y_{i}$
For e.g if the probabilities computed were p=[0.1, 0.7, 0.2] then this implies that the class with probability 0.7 is the likely class. This would imply that the ‘One hot encoding’ for yi would be yi=[0,1,0] therefore the gradient pi-yi = [0.1,-0.3,0.2]

<strong>Note: Further, we could extend this derivation for a Softmax activation output that outputs 3 classes
$S=\begin{pmatrix} \frac{e^{z1}}{e^{z1}+e^{z2}+e^{z3}}\\ \frac{e^{z2}}{e^{z1}+e^{z2}+e^{z3}} \\ \frac{e^{z3}}{e^{z1}+e^{z2}+e^{z3}} \end{pmatrix}$

We could derive
$\frac {\partial L}{\partial z1}= \frac {\partial L}{\partial p_{1}} \frac {\partial p_{1}}{\partial z_{1}} +\frac {\partial L}{\partial p_{2}} \frac {\partial p_{2}}{\partial z_{1}} +\frac {\partial L}{\partial p_{3}} \frac {\partial p_{3}}{\partial z_{1}}$ which similarly reduces to
$\frac {\partial L}{\partial z_{1}}=-\frac {y1}{p1} p1(1-p1) - \frac {y2}{p2}*(-p_{2}p_{1}) - \frac {y3}{p3}*(-p_{3}p_{1})$
$-y_{1}+ y_{1}p_{1} + y_{2}p_{1} + y_{3}p1 = p_{1}\sum (y_{1} + y_2 + y_3) - y_{1} = p_{1} - y_{1}$
Interestingly, despite the lengthy derivations the final result is simple and intuitive!

As seen in my post ‘Deep Learning from first principles with Python, R and Octave – Part 3 the key equations for forward and backward propagation are

Forward propagation equations layer 1
$Z_{1} = W_{1}X +b_{1}$ and $A_{1} = g(Z_{1})$
Forward propagation equations layer 1
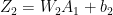$Z_{2} = W_{2}A_{1} +b_{2}$ and $A_{2} = S(Z_{2})$

Using the result (A) in the back propagation equations below we have
Backward propagation equations layer 2
$\partial L/\partial W_{2} =\partial L/\partial Z_{2}*A_{1}=(p_{2}-y_{2})*A_{1}$
$\partial L/\partial b_{2} =\partial L/\partial Z_{2}=p_{2}-y_{2}$
$\partial L/\partial A_{1} = \partial L/\partial Z_{2} * W_{2}=(p_{2}-y_{2})*W_{2}$
Backward propagation equations layer 1
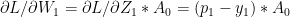
$\partial L/\partial W_{1} =\partial L/\partial Z_{1} *A_{0}=(p_{1}-y_{1})*A_{0}$
$\partial L/\partial b_{1} =\partial L/\partial Z_{1}=(p_{1}-y_{1})$

2.0 Spiral data set

As I mentioned earlier, I will be using the ‘spiral’ data from CS231n Convolutional Neural Networks to ensure that my vectorized implementations in Python, R and Octave are correct. Here is the ‘spiral’ data set.

import numpy as np
import matplotlib.pyplot as plt
import os
os.chdir("C:/junk/dl-4/dl-4")
exec(open("././DLfunctions41.py").read())

# Create an input data set - Taken from CS231n Convolutional Neural networks
# http://cs231n.github.io/neural-networks-case-study/
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# Plot the data
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.savefig("fig1.png", bbox_inches='tight')

The implementations of the vectorized Python, R and Octave code are shown diagrammatically below

2.1 Multi-class classification with Softmax – Python code

A simple 2 layer Neural network with a single hidden layer , with 100 Relu activation units in the hidden layer and the Softmax activation unit in the output layer is used for multi-class classification. This Deep Learning Network, plots the non-linear boundary of the 3 classes as shown below

import numpy as np
import matplotlib.pyplot as plt
import os
os.chdir("C:/junk/dl-4/dl-4")
exec(open("././DLfunctions41.py").read())

# Read the input data
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
  
# Set the number of features, hidden units in hidden layer and number of classess
numHidden=100 # No of hidden units in hidden layer
numFeats= 2 # dimensionality
numOutput = 3 # number of classes

# Initialize the model
parameters=initializeModel(numFeats,numHidden,numOutput)
W1= parameters['W1']
b1= parameters['b1']
W2= parameters['W2']
b2= parameters['b2']

# Set the learning rate
learningRate=0.6 

# Initialize losses
losses=[]
# Perform Gradient descent
for i in range(10000):
    # Forward propagation through hidden layer with Relu units
    A1,cache1= layerActivationForward(X.T,W1,b1,'relu')
    
    # Forward propagation through output layer with Softmax
    A2,cache2 = layerActivationForward(A1,W2,b2,'softmax')
    
    # No of training examples
    numTraining = X.shape[0]
    # Compute log probs. Take the log prob of correct class based on output y
    correct_logprobs = -np.log(A2[range(numTraining),y])
    # Conpute loss
    loss = np.sum(correct_logprobs)/numTraining
    
    # Print the loss
    if i % 1000 == 0:
        print("iteration %d: loss %f" % (i, loss))
        losses.append(loss)

    dA=0

    # Backward  propagation through output layer with Softmax
    dA1,dW2,db2 = layerActivationBackward(dA, cache2, y, activationFunc='softmax')
    # Backward  propagation through hidden layer with Relu unit
    dA0,dW1,db1 = layerActivationBackward(dA1.T, cache1, y, activationFunc='relu')
    
    #Update paramaters with the learning rate
    W1 += -learningRate * dW1
    b1 += -learningRate * db1
    W2 += -learningRate * dW2.T
    b2 += -learningRate * db2.T

#Plot losses vs iterations  
i=np.arange(0,10000,1000)
plt.plot(i,losses)

plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Losses vs Iterations')
plt.savefig("fig2.png", bbox="tight")

#Compute the multi-class Confusion Matrix
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

# We need to determine the predicted values from the learnt data
# Forward propagation through hidden layer with Relu units
A1,cache1= layerActivationForward(X.T,W1,b1,'relu')
    
# Forward propagation through output layer with Softmax
A2,cache2 = layerActivationForward(A1,W2,b2,'softmax')
#Compute predicted values from weights and biases
yhat=np.argmax(A2, axis=1)

a=confusion_matrix(y.T,yhat.T)
print("Multi-class Confusion Matrix")
print(a)

## iteration 0: loss 1.098507
## iteration 1000: loss 0.214611
## iteration 2000: loss 0.043622
## iteration 3000: loss 0.032525
## iteration 4000: loss 0.025108
## iteration 5000: loss 0.021365
## iteration 6000: loss 0.019046
## iteration 7000: loss 0.017475
## iteration 8000: loss 0.016359
## iteration 9000: loss 0.015703
## Multi-class Confusion Matrix
## [[ 99   1   0]
##  [  0 100   0]
##  [  0   1  99]]

Check out my compact and minimal book “Practical Machine Learning with R and Python:Second edition- Machine Learning in stereo” available in Amazon in paperback($10.99) and kindle($7.99) versions. My book includes implementations of key ML algorithms and associated measures and metrics. The book is ideal for anybody who is familiar with the concepts and would like a quick reference to the different ML algorithms that can be applied to problems and how to select the best model. Pick your copy today!!

2.2 Multi-class classification with Softmax – R code

The spiral data set created with Python was saved, and is used as the input with R code. The R Neural Network seems to perform much,much slower than both Python and Octave. Not sure why! Incidentally the computation of loss and the softmax derivative are identical for both R and Octave. yet R is much slower. To compute the softmax derivative I create matrices for the One Hot Encoded yi and then stack them before subtracting pi-yi. I am sure there is a more elegant and more efficient way to do this, much like Python. Any suggestions?

library(ggplot2)
library(dplyr)
library(RColorBrewer)

source("DLfunctions41.R")
# Read the spiral dataset
Z <- as.matrix(read.csv("spiral.csv",header=FALSE)) 
Z1=data.frame(Z)
#Plot the dataset
ggplot(Z1,aes(x=V1,y=V2,col=V3)) +geom_point() + 
  scale_colour_gradientn(colours = brewer.pal(10, "Spectral"))

# Setup the data
X <- Z[,1:2]
y <- Z[,3]
X1 <- t(X)
Y1 <- t(y)

# Initialize number of features, number of hidden units in hidden layer and
# number of classes
numFeats<-2 # No features
numHidden<-100 # No of hidden units
numOutput<-3 # No of classes

# Initialize model
parameters <-initializeModel(numFeats, numHidden,numOutput)

W1 <-parameters[['W1']]
b1 <-parameters[['b1']]
W2 <-parameters[['W2']]
b2 <-parameters[['b2']]

# Set the learning rate
learningRate <- 0.5
# Initialize losses
losses <- NULL
# Perform gradient descent
for(i in 0:9000){

# Forward propagation through hidden layer with Relu units
retvals <- layerActivationForward(X1,W1,b1,'relu')
A1 <- retvals[['A']]
cache1 <- retvals[['cache']]
forward_cache1 <- cache1[['forward_cache1']]
activation_cache <- cache1[['activation_cache']]

# Forward propagation through output layer with Softmax units
retvals = layerActivationForward(A1,W2,b2,'softmax')
A2 <- retvals[['A']]
cache2 <- retvals[['cache']]
forward_cache2 <- cache2[['forward_cache1']]
activation_cache2 <- cache2[['activation_cache']]

# No oftraining examples
numTraining <- dim(X)[1]
dA <-0

# Select the elements where the y values are 0, 1 or 2 and make a vector
a=c(A2[y==0,1],A2[y==1,2],A2[y==2,3])
# Take log
correct_probs = -log(a)
# Compute loss
loss= sum(correct_probs)/numTraining

if(i %% 1000 == 0){
sprintf("iteration %d: loss %f",i, loss)
print(loss)
}
# Backward propagation through output layer with Softmax units
retvals = layerActivationBackward(dA, cache2, y, activationFunc='softmax')
dA1 = retvals[['dA_prev']]
dW2= retvals[['dW']]
db2= retvals[['db']]
# Backward propagation through hidden layer with Relu units
retvals = layerActivationBackward(t(dA1), cache1, y, activationFunc='relu')
dA0 = retvals[['dA_prev']]
dW1= retvals[['dW']]
db1= retvals[['db']]

# Update parameters
W1 <- W1 - learningRate * dW1
b1 <- b1 - learningRate * db1
W2 <- W2 - learningRate * t(dW2)
b2 <- b2 - learningRate * t(db2)
}

## [1] 1.212487
## [1] 0.5740867
## [1] 0.4048824
## [1] 0.3561941
## [1] 0.2509576
## [1] 0.7351063
## [1] 0.2066114
## [1] 0.2065875
## [1] 0.2151943
## [1] 0.1318807

#Create iterations
iterations <- seq(0,10)
#df=data.frame(iterations,losses)
ggplot(df,aes(x=iterations,y=losses)) + geom_point() + geom_line(color="blue") +
    ggtitle("Losses vs iterations") + xlab("Iterations") + ylab("Loss")

plotDecisionBoundary(Z,W1,b1,W2,b2)

Multi-class Confusion Matrix

library(caret)
library(e1071)

# Forward propagation through hidden layer with Relu units
retvals <- layerActivationForward(X1,W1,b1,'relu')
A1 <- retvals[['A']]

# Forward propagation through output layer with Softmax units
retvals = layerActivationForward(A1,W2,b2,'softmax')
A2 <- retvals[['A']]
yhat <- apply(A2, 1,which.max) -1
Confusion Matrix and Statistics
          Reference
Prediction  0  1  2
         0 97  0  1
         1  2 96  4
         2  1  4 95

Overall Statistics                                        
               Accuracy : 0.96            
                 95% CI : (0.9312, 0.9792)
    No Information Rate : 0.3333          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.94            
 Mcnemar's Test P-Value : 0.5724          
Statistics by Class:

                     Class: 0 Class: 1 Class: 2
Sensitivity            0.9700   0.9600   0.9500
Specificity            0.9950   0.9700   0.9750
Pos Pred Value         0.9898   0.9412   0.9500
Neg Pred Value         0.9851   0.9798   0.9750
Prevalence             0.3333   0.3333   0.3333
Detection Rate         0.3233   0.3200   0.3167
Detection Prevalence   0.3267   0.3400   0.3333
Balanced Accuracy      0.9825   0.9650   0.9625

My book “Practical Machine Learning with R and Python” includes the implementation for many Machine Learning algorithms and associated metrics. Pick up your copy today!

2.3 Multi-class classification with Softmax – Octave code

A 2 layer Neural network with the Softmax activation unit in the output layer is constructed in Octave. The same spiral data set is used for Octave also
source("DL41functions.m") # Read the spiral data data=csvread("spiral.csv"); # Setup the data X=data(:,1:2); Y=data(:,3); # Set the number of features, number of hidden units in hidden layer and number of classes numFeats=2; #No features numHidden=100; # No of hidden units numOutput=3; # No of classes # Initialize model [W1 b1 W2 b2] = initializeModel(numFeats,numHidden,numOutput); # Initialize losses losses=[] #Initialize learningRate learningRate=0.5; for k =1:10000 # Forward propagation through hidden layer with Relu units [A1,cache1 activation_cache1]= layerActivationForward(X',W1,b1,activationFunc ='relu'); # Forward propagation through output layer with Softmax units [A2,cache2 activation_cache2] = layerActivationForward(A1,W2,b2,activationFunc='softmax'); # No of training examples numTraining = size(X)(1); # Select rows where Y=0,1,and 2 and concatenate to a long vector a=[A2(Y==0,1) ;A2(Y==1,2) ;A2(Y==2,3)]; #Select the correct column for log prob correct_probs = -log(a); #Compute log loss loss= sum(correct_probs)/numTraining; if(mod(k,1000) == 0) disp(loss); losses=[losses loss]; endif dA=0; # Backward propagation through output layer with Softmax units [dA1 dW2 db2] = layerActivationBackward(dA, cache2, activation_cache2,Y,activationFunc='softmax'); # Backward propagation through hidden layer with Relu units [dA0,dW1,db1] = layerActivationBackward(dA1', cache1, activation_cache1, Y, activationFunc='relu'); #Update parameters W1 += -learningRate * dW1; b1 += -learningRate * db1; W2 += -learningRate * dW2'; b2 += -learningRate * db2'; endfor # Plot Losses vs Iterations iterations=0:1000:9000 plotCostVsIterations(iterations,losses) # Plot the decision boundary plotDecisionBoundary( X,Y,W1,b1,W2,b2)

The code for the Python, R and Octave implementations can be downloaded from Github at Deep Learning – Part 4

Conclusion

In this post I have implemented a 2 layer Neural Network with the Softmax classifier. In Part 3, I implemented a multi-layer Deep Learning Network. I intend to include the Softmax activation unit into the generalized multi-layer Deep Network along with the other activation units of sigmoid,tanh and relu.

Stick around, I’ll be back!!
Watch this space!

References
1. Deep Learning Specialization
2. Neural Networks for Machine Learning
3. CS231 Convolutional Neural Networks for Visual Recognition
4. Eli Bendersky’s Website – The Softmax function and its derivative
5. Cross Validated – Backpropagation with Softmax / Cross Entropy
6. Stackoverflow – CS231n: How to calculate gradient for Softmax loss function?
7. Math Stack Exchange – Derivative of Softmax
8. The Matrix Calculus for Deep Learning